Применение метода симметричных составляющих
К АНАЛИЗУ НЕСИММЕТРИЧНЫХ ТРЕХФАЗНЫХ ЦЕПЕЙ
Методические указания
При подготовке к занятию необходимо ознакомиться с соответствующими разделами теории по учебной литературе: [1, c.293–299]; [3, c.188–198].
Ответьте на вопросы:
1. Какие преимущества имеет метод симметричных составляющих перед другими методами анализа несимметричных режимов?
2. Что собой представляют расчетные схемы при использовании метода симметричных составляющих?
3. Сформируйте системы напряжений (токов) прямой, обратной и нулевой последовательностей фаз.
Укажите, в каком соотношении находятся между собой напряжения отдельных фаз каждой из последовательностей: прямой ( 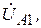
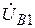 ,
, 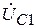 ), обратной (
), обратной ( 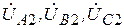 ), нулевой (
), нулевой ( 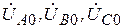 ). Аналогично для токов.
). Аналогично для токов.
4. Покажите, как вычисляются симметричные составляющие напряжений (токов) обратной и нулевой последовательности фаз, если известны несимметричные системы напряжений (токов) фаз.
5. Содержит ли ток нулевого провода несимметричной трехфазной четырехпроводной системы симметричные составляющие прямой и обратной последовательностей фаз?
Как определить ток нулевого провода через симметричные составляющие?
6. Чему равна величина симметричной составляющей нулевой последовательности фаз несимметричной системы линейных напряжений?
7. Устройство представляет собой трехфазный реостатный нагреватель, сопротивление каждой фазы R. Включен по схеме звезды. Каковы фрагменты такого участка одноименных схем замещения для каждой из симметричных составляющих: прямой, обратной, нулевой?
Это же устройство собрано по схеме треугольника. Тогда каков ответ на тот же вопрос?
8. В каком смысле можно использовать термины – продольная несимметрия, поперечная несимметрия?
9. Сформулируйте порядок расчета несимметричных режимов методом симметричных составляющих.
При изучении теоретического материала для подготовки к аудиторному занятию рекомендуется особо обратить внимание на 2 частных случая несимметрии: продольной – обрыв линейного провода, поперечной – короткое замыкание между линейным проводом и землей.
При расчетах этих режимов следует учесть следующее. В методе симметричных составляющих обычно несимметричные участки трехфазной цепи, в соответствии с теоремой о компенсации, эквивалентно заменяют соответствующими несимметричными источниками трехфазных напряжений. Так, в случае продольной несимметрии эквивалентный источник, 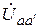 ,
, 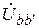 ,
, 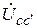 включают в рассечку трехфазной линии (рис.13.1), а в случае поперечной несимметрии эквивалентный источник
включают в рассечку трехфазной линии (рис.13.1), а в случае поперечной несимметрии эквивалентный источник 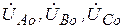 – между линейными проводами и «землей» (рис.13.2)
– между линейными проводами и «землей» (рис.13.2)
На рис.13.3 приведены расчетные схемы продольной несимметрии для прямой (13.3,а), обратной (13.3,б) и нулевой (13.3,в) последовательностей при симметричном источнике трехфазного напряжения прямой последовательности фаз.
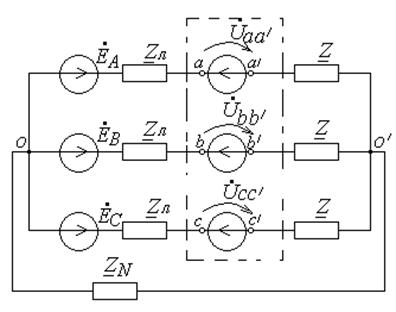
Рис.13.1. Продольная несимметрия
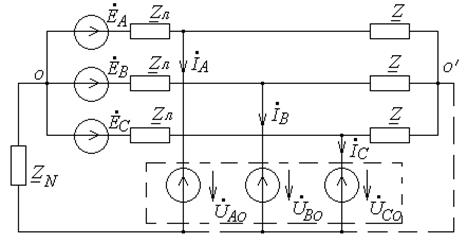
Рис.13.2. Поперечная несимметрия
При обрыве линейного провода аа’ дополнительные уравнения и уравнения Кирхгофа могут быть представлены как 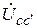 =0,
=0, 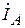 =0,
=0, 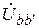 =0, что с учетом несимметрии токов и напряжений может быть записано как
=0, что с учетом несимметрии токов и напряжений может быть записано как
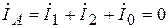 ,
,
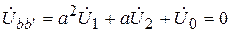 ,
,
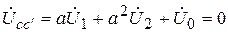 .
.
Таким образом, совместное решение уравнений, составленных для схем (рис.13.3) на основе законов Кирхгофа и уравнений, полученных из дополнительных условий, дает возможность определить 6 неизвестных симметричных составляющих 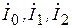
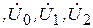 , а через них найти неизвестные токи, напряжения.
, а через них найти неизвестные токи, напряжения.
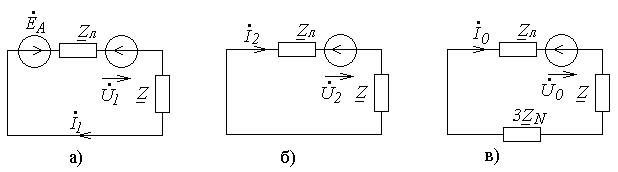
Рис.13.3. Расчетные схемы различных последовательностей при продольной несимметрии в цепи: а) прямой; б) обратной; в) нулевой
Расчетные схемы поперечной несимметрии для прямой (13.4,а), обратной (13.4,б) и нулевой (13.4,в) последовательностей фаз приведены на рис.13.4.
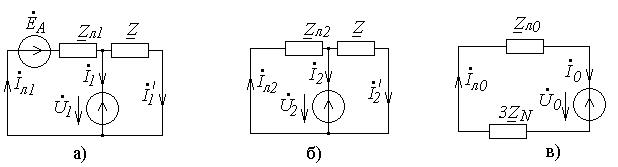
Рис.13.4. Расчетные схемы для различных последовательностей при поперечной
несимметрии в цепи: а) прямой; б) обратной; в) нулевой
При выполнении эквивалентных преобразований схемы на рис.13.4,а,б могут быть представлены в виде, показанном на рис.13.5,а,б,
где 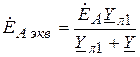 , а
, а 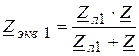 ,
, 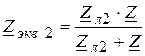 ,
, 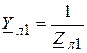 ,
, 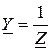 .
.
При замыкании точки а на землю дополнительные условия могут быть записаны как 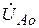 =0,
=0, 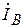 =0,
=0, 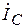 =0, что с учетом несимметрии токов и напряжений можно представить в виде:
=0, что с учетом несимметрии токов и напряжений можно представить в виде:
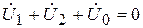 ,
,
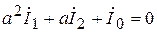 ,
,
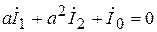 .
.

Рис.13.5. Преобразованные схемы прямой (а) и обратной (б) последовательностей
Решение системы 6 уравнений, составленной на базе схем рис.13.4, 13.5 и с учетом дополнительных условий, позволяет определить 6 неизвестных 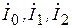
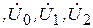 , а через них рассчитать неизвестные токи и напряжения.
, а через них рассчитать неизвестные токи и напряжения.
З а д а ч а 13.1
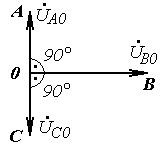
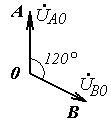
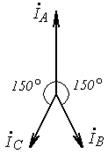
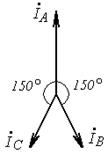
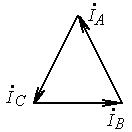
Разложите на симметричные составляющие указанные в табл.13.1, несимметричные системы векторов (задачу решите аналитически и графически).
Таблица 13.1
Исходные данные к задаче 13.1
| Вариант | Расположение векторов | Модули векторов |
 | 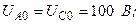 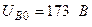 | |
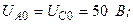 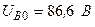 | ||
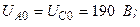 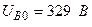 | ||
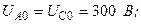 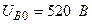 | ||
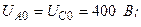 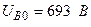 | ||
 | 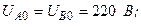 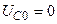 | |
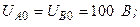 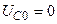 | ||
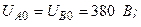 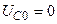 | ||
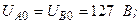 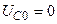 | ||
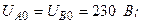 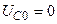 | ||
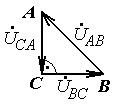 | 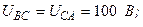 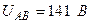 | |
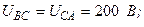 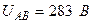 | ||
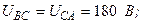 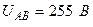 | ||
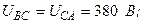 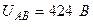 | ||
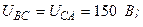 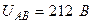 | ||
 | 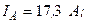 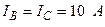 | |
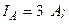 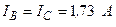 | ||
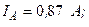 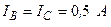 | ||
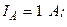 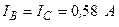 | ||
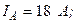 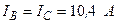 |
Окончание табл.13.1
| Вариант | Расположение векторов | Модули векторов |
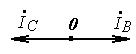 | 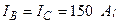 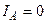 | |
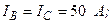 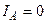 | ||
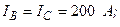 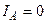 | ||
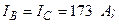 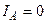 | ||
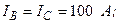 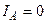 | ||
 | 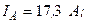 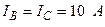 | |
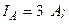 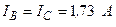 | ||
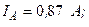 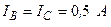 | ||
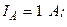 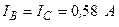 | ||
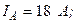 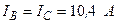 | ||
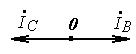 | 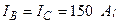 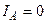 | |
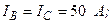 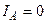 | ||
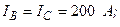 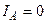 | ||
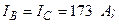 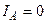 | ||
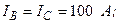 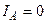 | ||
 | 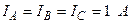 | |
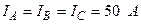 | ||
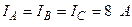 | ||
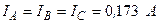 | ||
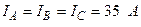 |
З а д а ч а 13.2
Несимметричная система напряжений 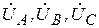 разложена на симметричные составляющие
разложена на симметричные составляющие 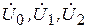 (за основу принят вектор
(за основу принят вектор 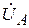 ). Определите комплексные значения этих несимметричных напряжений (табл.13.2).
). Определите комплексные значения этих несимметричных напряжений (табл.13.2).
Таблица 13.2
Исходные данные к задаче 13.2
| Вариант | 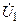 , В , В | 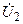 , В , В | 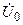 , В , В | Определить | Вариант | 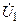 , В , В | 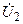 , В , В | 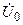 , В , В | Определить |
| –j120 | j100 | j100 | 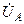 | 1Ð600 | j2 | –1 | 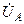 | ||
| –j120 | 20Ð200 | j100 | 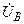 | –j | 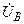 | ||||
| 30Ð450 | j50 | –j70 | 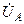 | 8Ð3000 | 8Ð600 | 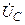 | |||
| 30Ð300 | –j10 | 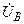 | 4Ð450 | 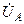 | |||||
| j200 | –j100 | 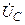 | –j | 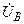 | |||||
| 10Ð300 | 10Ж300 | –20 | 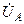 | –220 | 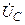 | ||||
| –50 | j30 | 30Ð300 | 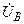 | j100 | –j100 | 100Ð600 | 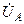 | ||
| –j10 | 20Ð1200 | j30 | 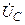 | j30 | j60 | 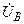 | |||
| 1Ð300 | j0,5 | 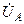 | –10 | 20Ð450 | 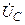 | ||||
| 30Ð600 | –50 | j20 | 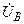 | j | –j | 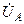 | |||
| 40Ð2100 | 40Ð300 | 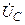 | –2 | –j2 | 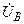 | ||||
| 8Ð300 | j4 | 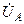 | j15 | 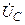 | |||||
| 10Ð1500 | –10 | 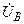 | –j10 | 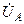 | |||||
| j6 | 6Ð450 | 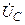 | 15Ð300 | –10 | 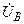 | ||||
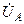 | 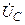 |
З а д а ч а 13.3
В трехфазном генераторе (рис.13.6), работающем в режиме холостого хода, произошло короткое междуфазное замыкание (место к.з. указано в табл.13.3). Определите действующие значения составляющих токов прямой, обратной и нулевой последовательностей фаз в образовавшейся несимметричной системе токов 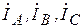 .
.
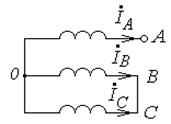
Рис.13.6. Схема к задаче 13.3
Таблица 13.3
Исходные данные к задаче 13.3
| Вариант | 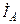 , А , А | 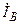 , А , А | 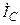 , А , А | к. з. фазы | Вариант | 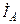 , А , А | 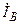 , А , А | 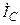 , А , А | к. з. фазы |
| – | B,C | – | А,В | ||||||
| – | A,B | – | В,С | ||||||
| – | А,В | – | C,A | ||||||
| – | А,С | – | A,B | ||||||
| – | В,С | – | B,C | ||||||
| – | А,С | – | C,A | ||||||
| – | А,В | – | A,B | ||||||
| – | В,С | – | B,C | ||||||
| – | С,А | – | C,A | ||||||
| – | А,В | – | A,B | ||||||
| – | В,С | – | B,C | ||||||
| – | С,А | – | C,A | ||||||
| – | А,В | – | A,B | ||||||
| – | В,С | – | B,C | ||||||
| – | С,А | – | C,A |
З а д а ч а 13.4
К симметричному генератору, сопротивлениями обмоток которого можно пренебречь, подключен трехфазный двигатель, обмотки которого соединены звездой, сопротивления различных последовательностей известны. Сопротивление нейтрального провода для всех вариантов одинаковое 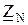 = j5 Ом. В одном из линейных проводов произошел обрыв (рис.13.7). Найдите величины токов и напряжений, указанные в табл.13.4.
= j5 Ом. В одном из линейных проводов произошел обрыв (рис.13.7). Найдите величины токов и напряжений, указанные в табл.13.4.
Таблица 13.4
Исходные данные к задаче 13.4
| Вариант | 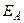 , В , В | 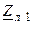 , Ом , Ом | 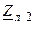 , Ом , Ом | 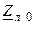 , Ом , Ом | 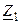 , Ом , Ом | 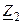 , Ом , Ом | 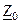 , Ом , Ом | Место обрыва | Определить |
| aа’ | 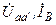 | ||||||||
| j 20 | j 20 | j 30 | j 50 | j 10 | j 5 | bb’ | 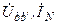 | ||
| j 5 | j 5 | j 20 | j 40 | j 20 | j 3 | cc’ | 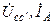 | ||
| j 10 | j 5 | j 20 | j 50 | j 40 | j 4 | aа’ | 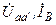 | ||
| j 20 | j 20 | j 40 | j 80 | j 60 | j 7 | bb’ | 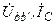 | ||
| j 20 | j 20 | j 10 | j 50 | j 10 | j 4 | cc’ | 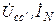 | ||
| j 10 | j 10 | j 20 | j 40 | j 30 | j 4 | aа’ | 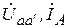 | ||
| j 5 | j 5 | j 10 | j 20 | j 10 | j 4 | bb’ | 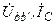 | ||
| j 40 | j 40 | j 10 | j 60 | j 30 | j 3 | cc’ | 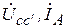 | ||
| j 8 | j 4 | j 10 | j 20 | j 10 | j 3 | aа’ | 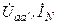 | ||
| j 20 | j 20 | j 30 | j 70 | j 60 | j 4 | bb’ | 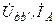 | ||
| j 20 | j 20 | j 30 | j 60 | j 30 | j 2 | cc’ | 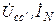 | ||
| j 10 | j 10 | j 2 | j 5 | j 4 | j 2 | aа’ | 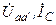 | ||
| j 10 | j 20 | j 20 | j 80 | j 60 | j 2 | bb’ | 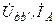 | ||
| j 20 | j 20 | j 30 | j 10 | j 60 | j 2 | cc’ | 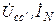 | ||
| j 40 | j 40 | j 50 | j 100 | j 80 | j 6 | aа’ | 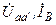 | ||
| j 20 | j 20 | j 30 | j 80 | j 40 | j 5 | bb’ | 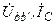 | ||
| j 20 | j 20 | j 30 | j 60 | j 40 | j 5 | cc’ | 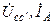 | ||
| j 10 | j 10 | j 20 | j 50 | j 40 | j 6 | aа’ | 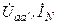 |
Окончание табл.13.4
| Вариант | 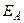 , В , В | 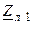 , Ом , Ом | 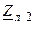 , Ом , Ом | 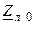 , Ом , Ом | 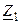 , Ом , Ом | 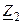 , Ом , Ом | 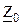 , Ом , Ом | Место обрыва | Определить |
| j 10 | j 10 | j 20 | j 60 | j 30 | j 5 | bb’ | 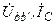 | ||
| j 20 | j 20 | j 40 | j 50 | j 20 | j 3 | cc’ | 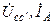 | ||
| j 10 | j 10 | j 20 | j 8 | j 40 | j 4 | aа’ | 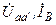 | ||
| j 10 | j 10 | j 20 | j 60 | j 50 | j 3 | bb’ | 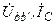 | ||
| j 10 | j 10 | j 20 | j 60 | j 50 | j 3 | cc’ | 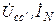 | ||
| j 10 | j 10 | j 20 | j 80 | j 40 | j 7 | aа’ | 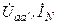 | ||
| j 10 | j 10 | j 20 | j 60 | j 30 | j 4 | bb’ |  | ||
| j 5 | j 5 | j 10 | j 50 | j 40 | j 5 | cc’ |  | ||
| j 10 | j 10 | j 20 | j 40 | j 20 | j 3 | aа’ |  | ||
| j 10 | j 10 | j 20 | j 80 | j 40 | j 5 | bb’ |  | ||
| j 5 | j 5 | j 10 | j 40 | j 20 | j 3 | cc’ | 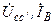 |
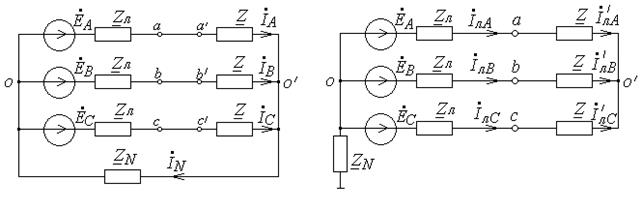
Рис.13.7. Схема к задаче 13.4 Рис.13.8. Схема к задаче 13.5
З а д а ч а 13.5
К симметричному генератору подключен трехфазный двигатель, обмотки которого соединены звездой. Один из линейных проводов в точке, указанной в таблице, замкнут на землю. Найдите напряжения и токи, указанные в табл.13.5. Для всех вариантов одинаковое 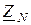 = j5 Ом.
= j5 Ом.
Таблица 13.5
Исходные данные к задаче 13.5
| Вариант | 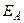 , В , В | 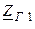 , Ом , Ом | 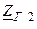 , Ом , Ом | 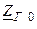 , Ом , Ом | 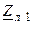 , , 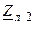 Ом Ом | 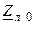 , Ом , Ом | 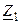 , Ом , Ом | 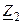 , Ом , Ом | точка к. з. | Определить |
| j 5 | j 2 | j 0,5 | j 1 | j 0,5 | 5+j 5 | 1+j 2 | a | 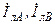 | ||
| j 4 | j 2 | j 1 | j 1 | j 0,5 | 3+j 4 | 1+j 1 | b | 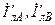 | ||
| j 6 | j 3 | j 1 | j 2 | j 1 | 2+j 4 | 1+j 2 | c | 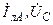 | ||
| j 5 | j 4 | j 1 | j 2 | j 1 | 4+j 4 | 2+j 2 | a | 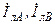 | ||
| j 6 | j 3 | j 2 | j 2 | j 1 | 3+j 3 | 1+j 1 | b | 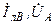 | ||
| j 7 | j 4 | j 2 | j 1 | j 0,5 | j 5 | j 2 | c | 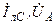 | ||
| j 8 | j 6 | j 1,5 | j 2 | j 1 | j 6 | j 3 | a | 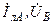 | ||
| j 8 | j 6 | j 2 | j 3 | j 1,5 | j 8 | j 4 | b | 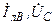 | ||
| j 6 | j 3 | j 1 | j 3 | j 1 | 4+j 4 | 1+j 2 | c | 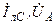 | ||
| j 8 | j 4 | j 2 | j 2 | j 1 | 3+j 3 | 1+j 1 | a | 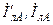 | ||
| j 4 | j 2 | j 0,5 | j 1 | j 0,5 | 2+j 2 | 1+j 2 | b | 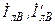 | ||
| j 3,5 | j 1,5 | j 0,75 | j 0,8 | j 0,8 | 3+j 3 | 2+j 1 | c | 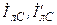 | ||
| j 8 | j 6 | j 4 | j 2 | j 3 | 4+j 4 | 2+j 2 | a | 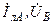 |
Окончание табл.13.5
| Вариант | 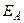 , В , В | 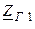 , Ом , Ом | 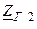 , Ом , Ом | 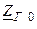 , Ом , Ом | 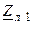 , , 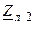 Ом Ом | 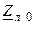 , Ом , Ом | 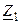 , Ом , Ом | 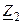 , Ом , Ом | точка к. з. | Определить |
| j 10 | j 5 | j 5 | j 3 | j 2 | 9+j 9 | 8+j 6 | b | 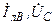 | ||
| j 9 | j 6 | j 3 | j 2 | j 1 | 8+j 8 | 4+j 3 | c | 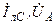 | ||
| j 8 | j 4 | j 2 | j 1 | j 1,5 | 3+j 4 | 1+j 2 | a | 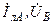 | ||
| j 7 | j 3 | j 2 | j 1 | j 0,8 | 4+j 5 | 1+j 2 | b | 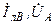 | ||
| j 6 | j 3 | j 1 | j 0,5 | j 1 | 2+j 3 | 1+j 2 | c | 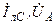 | ||
| j 5 | j 4 | j 1 | j 0,5 | j 0,8 | 3+j 4 | 1+j 2 | a | 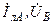 | ||
| j 6 | j 4 | j 2 | j 1 | j 1 | 2+j 1 | 1+j 2 | b | 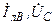 | ||
| j 2 | j 1 | j 0,5 | j 0,3 | j 0,5 | 1+j 2 | 2+j 1 | c | 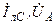 | ||
| j 3 | j 2 | j 1 | j 0,5 | j 0,5 | 3+j 3 | 1+j 1 | a | 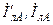 | ||
| j 2 | j 1 | j 1 | j 0,5 | j 0,5 | 3+j 4 | 1+j 1 | b | 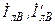 | ||
| j 4 | j 2 | j 2 | j 1 | j 1,5 | 2+j 4 | 1+j 2 | c | 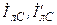 | ||
| j 6 | j 3 | j 1 | j 0,5 | j 0,5 | 2+j 2 | 1+j 2 | a | 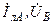 | ||
| j 4 | j 3 | j 1,5 | j 0,8 | j 1 | 1+j 1 | 1+j 2 | b | 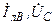 | ||
| j 5 | j 4 | j 2 | j 1 | j 1 | 2+j 2 | 1+j 2 | c | 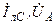 | ||
| j 6 | j 5 | j 1 | j 0,8 | j 0,8 | j 3 | 1+j 2 | a | 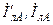 | ||
| j 4 | j 2 | j 2 | j 1 | j 1,5 | j 4 | 1+j 2 | b | 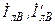 | ||
| j 4 | j 3 | j 1 | j 0,8 | j 0,5 | j 5 | j 2,5 | c | 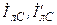 |
ЗАНЯТИЕ 14
