Преобразование Лапласа

В теории автоматического управления широко используется специальный метод прикладного анализа – операционное исчисление, в основе которого лежит функциональное преобразование Лапласа.

Сущность операционного метода заключается в использовании прямого преобразовании Лапласа (ППЛ), которое некоторой функции 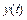действительной переменной 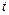ставит в соответствие функцию 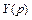комплексной переменной :

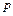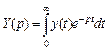, (1.5)

где 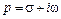– переменная (множитель) Лапласа.

Условием существования преобразования Лапласа является сходимость интеграла в правой части равенства (1.5). Минимальное значение параметра s, при котором данный интеграл сходится, носит название абсциссы сходимости.

Обратное преобразование Лапласа (ОПЛ)имеет вид:

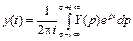. (1.6)

Функция 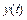носит называние оригинала, а функция 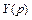– изображения.

Для пары преобразований Лапласа используется также операторная форма записи:

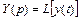и

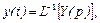
где L – оператор Лапласа.

Вычисление интегралов (1.5), (1.6) для некоторых видов функций может оказаться трудным или громоздким, поэтому для упрощения расчетов используют таблицы соответствий «оригинал–изображение» (таблица 1).

Таблица 1 – Таблица оригиналов и их изображений ( 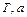– const)

Оригинал	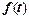Изображение F(p)

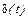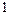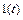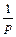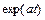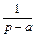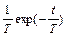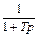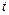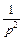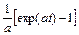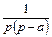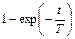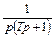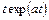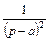Свойства преобразования Лапласа:

1. Изображение суммы функций равно сумме изображений отдельных функций:

.

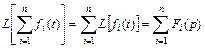2. Временному запаздыванию функции в области оригиналов соответствует умножение ее изображения на множитель 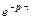, где 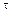– время запаздывания:

.

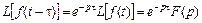3. При нулевых начальных условиях дифференцирование в области оригиналов соответствует в области изображений умножению изображения функции на переменную Лапласа в степени, соответствующей порядку производной:

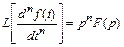при условии, что 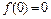, 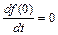и т.д.

При ненулевых начальных условиях правило расчета изображения для производной 1-го порядка имеет вид:

.

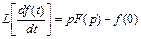4. Интегрирование в области оригиналов соответствует делению на переменную Лапласа 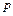в области изображений:

.

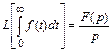5. Постоянная величина выносится за знак преобразования:

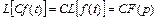, где .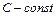

6. По виду изображения 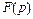можно судить о начальном (при 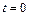) и предельном (при 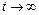) значениях оригинала 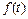(теоремы о начальном и конечном значениях):

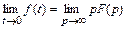и .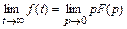

С помощью преобразования Лапласа существенно упрощается процедура решения дифференциальных или интегродифференциальных уравнений с постоянными коэффициентами.

Выделяют следующие этапы решения:

1) преобразование заданного дифференциального уравнения по Лапласу, учитывая при этом начальные условия (то есть переход из области оригиналов в область изображений);

2) решение полученного алгебраического уравнения относительно изображения;

3) переход от изображения решения к его оригиналу (например, с помощью таблиц преобразования Лапласа).

Пример 4.Решить операторным методом Лапласа следующее дифференциальное уравнение (при нулевом начальном условии):

, .

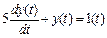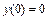Выполним прямое преобразование Лапласа над исходным уравнением:

.

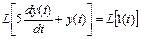Учитывая 1-е свойство преобразования Лапласа, получим в левой части уравнения два слагаемых:

.

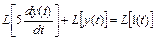Применив 3-е и 5-е свойства к первому слагаемому в левой части уравнения и используя таблицу преобразований Лапласа для элемента в правой части уравнения, получим следующий результат:

.

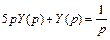Далее решим уравнение относительно изображения:

,

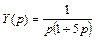откуда по таблице преобразований Лапласа находим решение исходного дифференциального уравнения:

.

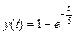Пример 5.Найти оригинал функции 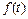, зная ее изображение: .

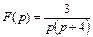По таблице 1 можно найти оригинал функции

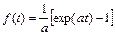
для изображения 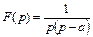, которое отличается от заданного по условию.

Поэтому заданное выражение изображения необходимо преобразовать к табличному виду, учитывая 5-е свойство преобразования Лапласа:

.

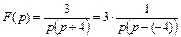В результате для искомого оригинала получим:

.
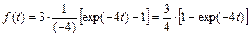