Опуклість і угнутість графіка функції. Точки перегину

Графік функції 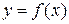, яка диференційовна на інтервалі 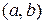, називається опуклим вниз (угнутим) на інтервалі 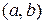, якщовін розташований вище будь-якої її дотичної на цьому інтервалі. Графік функції 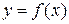називається опуклим вгору на інтервалі 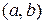, якщо він розташований нижче будь-якої її дотичної на цьому інтервалі.

Точка графіка неперервної функції 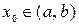, яка відділяє його частини різної опуклості, називається точкою перегину.

На рисунку 2.10 крива 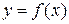опукла вгору в інтервалі 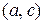, опукла вниз в інтервалі 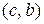точка ) — точка 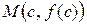перегину.

Інтервали опуклості вниз і вгору знаходять за допомогою наступних теорем.

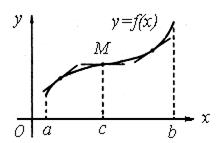
Рис. 2.10

Теорема 1. Якщо функція 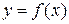, у всіх точках інтервалу 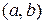має від’ємну другу похідну, тобто 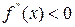, то графік функції в цьому інтервалі опуклий вгору. Якщо ж 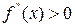у всіх точках інтервалу 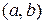, то графік функції 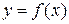— опуклий вниз.

Теорема 2 (достатня умова існування точок перегину). Якщо друга похідна 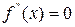або не існує в точці 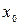і під час переходу через точку 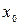змінює знак, то точка графіка функції 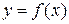з абсцисою 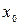є точка перегину.

Точки, в яких 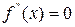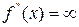, або , або 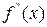не існує (ні скінченна, ні нескінченна) називають критичними точками 2-го роду.

Приклад 2.52. Знайти точки перегину кривої у = ln(4 + х²).

Розв’язання. Знаходимо другу похідну:

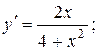
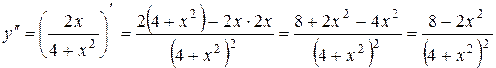
у¢¢ = 0 при х = ±2. Це абсциси точок, «підозрілих» на перегин (критичні точки 2-го роду). Інших критичних точок 2-го роду немає. Досліджуємо точки х = ±2, для чого складемо таблицю (таблиця 2). Тому що при переході через точки х = ±2 у¢¢ змінює знак, то точки з абсцисами х = ±2є точками перегину.

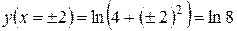. Отже, точки А(+2, ln 8), В(-2, ln 8) – точки перегину графіка функції у = ln(4 + х²).

Таблиця 2

x	(-¥; -2)	-2	(-2; 2)		(2; ¥)
у¢¢	-		+		-
Графік у	опуклий	Точка перегину	угнутий	Точка перегину	опуклий

Зауважимо, що таблиця містить також інтервали опуклості й угнутості графіка функції. В інтервалах при 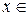(- ¥, -2), (2, ¥) графік опуклий (у¢¢ < 0), в інтервалі 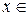(-2, 2) графік угнутий (у¢¢ > 0).

Асимптоти кривої

Пряма називається асимптотоюкривої, якщо відстань від точки М кривої до цієї прямої наближається до нуля при віддаленні точки М в нескінченність уздовж кривої. Інакше кажучи, крива у = f(x), яка має нескінчену гілку,необмежено наближається до своєї асимптоти при віддаленні змінної х у нескінченність (рис 2.11).

Рис. 2.11.

Асимптоти бувають вертикальні, горизонтальні та похилі.

1. Якщо в точці х₀ =а функція має розрив другого роду, то пряма х = а може бути вертикальною асимптотою графіка функції.

2. Якщо при 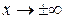дляфункції існує скінченна границя, тобт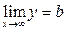о або 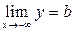то пряма 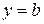є горизонтальною асимптотою графіка функції.

3. Рівняння будь-якої похилої асимптоти має вид:

y = kx+ b .(2.20)

Для визначення похилої асимптоти до графіка функції у = f(x), треба знайти числа k та b за формулами:

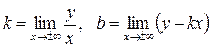. (2.21)

Границі треба обчислювати окремо для випадків 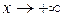, та 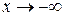, але часто ці границі збігаються.

Зауваження.Якщо хоча б одна з цих границь 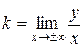не існує, то похилих асимптот не існує. Зауважимо також, що горизонтальні асимптоти є окремим випадком похилих асимптот при k = 0.

Приклад 2.53. Знайти асимптоти до графіка функції .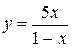

Розв’язання. При 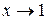функція у не існує і має розрив в точці х=1. Визначимо вид розриву, для чого знаходимо лівобічну та правобічну границі:

.

.

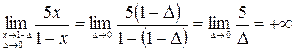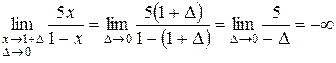В точці 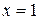функція має розрив другого роду, тому пряма 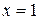є вертикальна асимптота.

Похилі асимптоти шукаємо у виді у = kx+ b.

визначаємо спочатку k

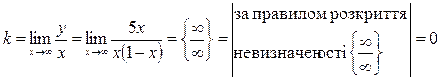
похила асимптота відсутня.

Знаходимо горизонтальні асимптоти: 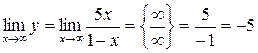. . 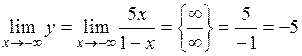Рівняння горизонтальної асимптоти .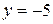