Приведите примеры линейных пространств

Вещественное линейное пространство, комплексное линейное пространство и т.д.

43. Какое линейное пространство называется n-мерным?

Так называется любое пространство, в котором существует линейно независимая система из 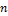векторов, а любая система из 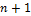вектора является линейно зависимой.

Дайте определение базиса n-мерного линейного пространства.

Это любая система из 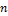линейно независимых векторов данного линейного пространства.

Сформулируйте теорему о разложении вектора по базису в n-мерном линейном пространстве.

Любой базис из 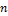-мерного линейного пространства можно представить, и притом только единственным способом, в виде линейной комбинации базисных векторов.

Дать определение координат вектора в линейном пространстве.

Координаты вектора – коэффициенты при базисных векторах в линейной комбинации.

Сформулируйте теорему о сведении внутренней и внешней операций над векторами к операциям над их координатами.

1) Суммой двух векторов является вектор, координатами которого являются суммы соответствующих координат слагаемых.

2) Произведением вектора на число является вектор, координатами которого являются произведения координат исходного вектора и данного числа.

Дайте определение минора порядка m матрицы А.

Это определитель подматрицы размера .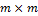

Дайте определение ранга матрицы.

Ранг матрицы – это количество линейно независимых векторов в матрице; наивысший порядок миноров матрицы, отличных от нуля.

Дайте определение базисного минора, базисных строк и столбцов матрицы.

Базисный минор – любой минор наивысшего порядка, отличный от нуля.

Базисные строки/столбцы – строки/столбцы матрицы, входящие в базис.

Сформулируйте теорему о базисном миноре.

Любая строка/столбец матрицы является линейной комбинацией её базисных строк/столбцов.

Сформулируйте правило, позволяющее определить линейно зависимые строки (столбцы) матрицы или нет.

Исходя из теоремы о базисном миноре, если строки/столбцы матрицы линейно зависимы, то определитель такой матрицы равен нулю.

Сформулируйте правило, позволяющее определить, является ли данная строка матрицы линейной комбинацией других строк или нет.

Исходя из теоремы о базисном миноре, если строка/столбец матрицы является линейной комбинацией других строк, то определитель такой матрицы равен нулю.

Сформулируйте теорему о необходимых и достаточных условиях равенства нулю определителя.

Определитель равен нулю, если система векторов матрицы является линейно зависимой.