Арапайым итерация әдісі

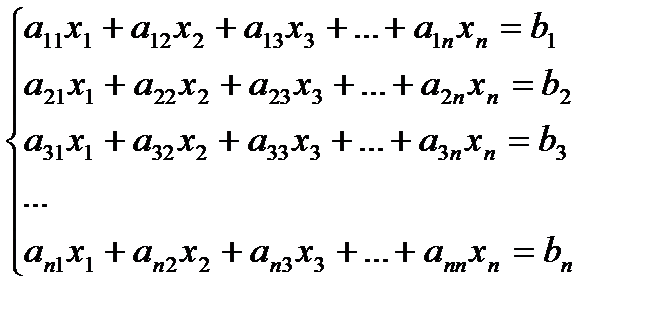(3.31)

(3.31)- жүйені қандай да бір амалдар қолданып келесі түрге келтірейік,

(3.32)

немесе қысқаша жазсақ:

(3.32) – жүйенің оң жағы n - өлшемді векторлық кеңістікте x(x₁,x₂,…,x_n) нүктесін осы кеңістіктің y(y₁,y_2,…,y_n) нүктесіне айналдыратын бейнелеу болып табылады:

(3.33)

(3.32) – жүйені қолданып, бастапқы нүктені таңдап алып n - өлшемді векторлық кеңістікте нүктелердің итерациялық тізбегін құруға болады:

(3.34)

(3.34) – итерациялық тізбек жинақты болса, оның шегі (3.32) итерациялық жүйенің шешімі болады. Тізбектің жинақтылығын дәлелдеу үшін функционалдық анализдің кейбір ұғымдары керек:

1-анықтама:

Х жиынының х және у нүктелерінің ара қашықтығын анықтайтын

функциясы метрика деп аталады, егер төмендегі шарттар

орындалса:

1 ;

2 , егер х=у болғанда ғана;

3 ;

4 ;

2-анықтама:

Метрикасы енгізілген жиын метрикалық кеңістік деп аталады.

3-анықтама:

Егер F толық метрикалық кеңістікте анықталған қысыңқы бейнелеу болса:

(3.35)

онда x=Fx болатын жалғыз қозғалмайтын нүкте табылады. Бұл жағдайда F бейнелеуіне құрылған итерациялық тізбек кез келген бастапқы жуықтауларда х нүктесіне жинақталады. Мұндағы: , , Fx, Fy- х,у нүктелерінің бейнелері.

4-анықтама: (қысыңқы бейнелеу принципі)

Сызықты алгебралық теңдеулер жүйесін төмендегі үш метрикалық кеңістікте қарастыруға болады:

(3.36)

(3.37)

(3.38)

(3.36) – метрикалық кеңістікте:

(3.39.)

теңсіздігі немесе (3.37) – метрикалық кеңістікте:

(3.40)

теңсіздігі немесе (3.38) - метрикалық кеңістікте:

(3.41)

теңсіздіктерінің ең болмағанда біреуі орындалса, онда (3.33) – теңдеумен берілген F бейнесі қысыңқы бейнелеу болады және итерациялық процесс кез келген бастапқы жуықтауларда өзінің жалғыз шешіміне жинақталады.

(3.32) – түріне келтірілген итерациялық жүйеге карапайым итерация әдісін қолданбас бұрын жүйенің матрицасының диагональды элементтерінің басым болғаны дұрыс. Яғни . Және коэффициенттер 1-ден кіші болуы керек: . Бұл шарттың орындалуы қысыңқылық шарттарды қанағаттандыратын қажетті шарт. Ал жеткіліктілік шарт (3.39) – (3.41.) шарттардың ең болмағанда біреуі орындалуы керек. Егер диагональдық басымдылық болмаса жүйеге қандай да бір ауыстырулар мен алмастырулар, арифметикалық амалдар қолдануға болады.

Әдісті қолдануға болады деген тұжырымға келгеннен кейін өзіміз бастапқы жуықтауларды таңдап алып итерациялық процесс құрамыз:

(3.41)

Егер е- дәлдікке дейін шешім табу керек болса, онда есептеу процесін

(3.42)

немесе

(3.43)

шарттары орандалғанша жалғастырады. Мұндағы - евклид кеңістігіндегі соңғы, көрші жуықтаулардың ара қашықтығы. Бастапқы жуықтаулар ретінде практикада көбіне жүйенің бос мүшелері алынады.

1- мысал:

-7х₁+4х₂ - 4х₃=-8

2х₁ - 6х₂ - х₃=-5

-2х₁ - х₂ +6х₃=3

Бұл жүйе матрицасында диагональдық басымдылық бар. (3.39) – (3.41) – шарттардың орындалуын ұйымдастыру керек. Ол үшін жүйенің матрицасын және бос мүшелер векторын

матрицасына көбейтейік:

.

Бұл жүйе үшін жинақтылық шарттар орындалады. Сондықтан жүйені итерациялық түрде жазамыз:

Итерацияның бастапқы жуықтаулары ретінде бос мүшелерін алайық: . Келесі жуықтаулар мына формуламен есептеледі:

, k=0,1,2,…,n

2-мысал:

Мұндағы теңдеулерді қолдануға оңай болуы үшін рим цифрларымен белгіледік. Диагональдық басымдылықты алу үшін (I) – теңдеудің орнына (II) – теңдеуді, ал 2-ші теңдеу етіп (I+II) – теңдеуін жазамыз, (III) – теңдеудің орнына (I ) теңдеуді жазамыз:

Бұл жүйеде диагональдық басымдылық бар. Сондықтан итерациялық түрге келтіру үшін жүйенің әр теңдеуін мүшелеп диагональдық элементіне бөлеміз де коэффициенті 1-ге тең белгісіздер арқылы өрнектейміз:

Жинақтылығын зерттейміз:

1-ші метрикалық кеңістікте:

жинақтылық шарты бұл кеңістікте орындалмайды екен.

2-ші метрикалық кеңістікте:

жинақтылық шарты орындалды.

3-ші метрикалық кеңістікте:

Жинақтылық шарты орындалатыны байқалды, яғни бастапқы жуықтаулар ретінде бос мүшелерді алып итерациялық процесс құрамыз:

; ; ;

k=0,1,2,…

шарты орындалғанша итерация жүреді.

Зейдель әдісі

(3.31)– жүйе (3.32) – итерациялық түрге келтірілсін. Бұл жүйені қарапайым итерация әдісімен шешкенде итерациялық процесстің әр қадамы белгілі бастапқы жуықтаудан белгісіздің жаңа жуықтауына көшуден тұратын еді. Белгілі бастапқы жуықтаудың элементтерін x₁, x₂, … , x_n деп, ал есептелетін келесі жуықтауларды y₁, y₂, … , y_n деп белгілейік. Сонда есептеу формулалары келесі түрге көшеді:

(3.46)

Зейдель әдісінің негізгі идеясы итерациялық процестің әр қадамында y_i-дің мәндерін есептеу барысында оның алдында есептелген y₁, y₂, … , y_i-1 мәндері қолданылады да (3.46)– ны ашып жазсақ, Зейдель формуласы келесідей болады:

(3,47 )

(3,47)– итерациялық процесінің жинақтылығы үш метрикалық кеңістікте мына шарттардың бірі орындалуымен бекітіледі:

кеңістікте

шарты (3.48)

кеңістікте

шарты (3.49)

кеңістікте

шарты (3.50)

Егер бұл шарттардың біреуі орындалса, (3.47)– итерациялық процесс кез келген бастапқы жуықтауда өзінің жалғыз шешіміне жинақталады.

Зейдель әдісін жүйенің матрицасы симметриялы элементтерден тұрған жағдайда қолданады. Егер матрица симметриялы болмаса оны симметриялы түрге келтіру үшін жүйенің матрицасын және векторларын транспонирленген матрицаға көбейтеді:

А^Т*А*х=A^T*b (3.51)

Белгілеулер енгіземіз:

A^T*A=C

A^T*b=D

Сонда

Cx=D (3.52)

(3.52) – жүйені қалыпты жүйе деп атайды. Қалыпты жүйенің элементтері симметриялы және диагональды элементтері нөлден өзгеше болады. Қалыпты жүйені алдында қарастырған амалдарды қолданып (3.47)– итерациялық жүйеге келтіруге болады.

(3.52) – қалыпты жүйеге эквивалентті (3.47)– келтірілген итерациялық жүйе үшін Зейдельдің итерациялық процесі өзінің жалғыз шешіміне кез келген бастапқы жуықтауларда жинақталады.

Егер е дәлдік берілсе, итерациялық әдіс , i=0,1,2,… шарты орындалғанға дейін жалғасады.

1-мысал:

Берілген жүйе үшін матрицасын, транспонирленген матрицасын құрып, жоғарыда айтылған әрекеттерді орындаймыз:

, , .

. .

Сонымен анықталған матрица бойынша қалыпты жүйе құраймыз:

Итерациялық түрге келтіреміз:

Бұл жүйе үшін (3.48)– (3.50)– жинақтылық шарттары орынды. Ендеше бастапқы жуықтау таңдаймыз: х₁=1, х₂=1, х₃=1.

Зейдель процесі келесідей жазылады:

Есептеу , i=0,1,2,… шарты орындалғанға дейін жалғасады.

2.5 Қуалау әдісі

Математикалық физиканың есептері көбінде үш диагональді сызықты алгебралық теңдеулер жүйесінің шешімін табуға шектеледі, үш диагоналді сызықты алгебралық теңдеулер жүйесінің теңдеулерінде тек қана үш айнымалылардың коэффициенттері нөлге тең емес, қалған коэффициенттер нөлге тең.

(18)

Сондай жүйенің матрицасы үш диагоналді:

Үш диагоналді сызықты алгебралық теңдеулер жүйесін шешу тиімді әдісі болып қуалау әдісі табылады.

Қуалау әдісінің бірінші кезеңі – тура қуалау. Қуалау коэффициенттері келесі формулалармен табылады:

. (19)

Қуалау әдісінің екінші кезеңі – кері қуалау. Кері бағытта функцияның мәндері табылады:

. (20)

Қуалау әдісін қолдану үшін әдістің жинақтылығы болуы керек. Жиынактылық шарты :

. (21)

Мысал 4

Жүйені қуалау әдісімен шеш.

Шешім:

Қуалау әдісін қолдану үшін әдістің жинақтылығы болуы керек. Жиынактылық шарты орындалады:

.

Негізгі диагональ элементтері басқа элементтер қосындысынан кем емес, мысал 2,3>1+1,1.

Сонымен, қуалау әдісін қолдануға болады.

.

4 кестеде қуалау әдісін қолданудың натижесі көрсетілген.

4 - кесте. Қуалау әдісін қолдану.

i	ai	ci	bi	fi	αi	βi	yi
	1,00	-0,18	0,00	-0,09	-	-	0,16
	1,00	-2,30	1,10	2,00	-0,18	0,09	-0,39
	1,10	-3,30	1,50	-1,00	-0,52	-0,99	-1,15
	1,20	-2,80	1,30	-2,30	-0,55	0,76	3,49
	1,20	-2,90	1,50	4,10	-0,61	0,65	-4,68
	2,50	-3,80	1,20	0,20	-0,69	-2,25	3,53
	1,30	-2,60	1,00	-4,20	-0,58	2,61	-1,58
	1,20	-2,40	1,00	-3,20	-0,54	0,44	3,73
	0,00	-0,20	1,00	3,10	-0,57	1,53	-3,85