Дослідження загального рівняння прямої

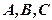Корисно знати особливості розміщення прямої в окремих випадках, коли одне або двоє з чисел дорівнюють нулю.

1. 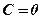. Загальне рівняння має вигляд: 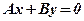. Йому задовольняє точка 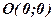, отже, пряма проходить через початок координат. Його можна записати .

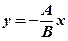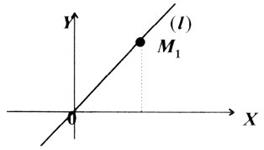
На рис.3 вважаємо що

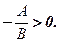
Рис. 3.

Якщо покласти 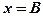, то 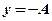, маємо ще одну точку 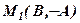(див. рис.3)

2. , тоді рівняння має вигляд 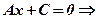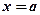, де 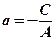. Нормальний вектор 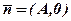лежить на осі 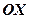, пряма 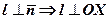. Таким чином, пряма 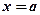перпендикулярна 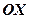в точці 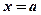, або ж паралельна осі 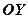(див. рис. 4).

Зокрема, якщо і 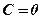, то 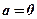і рівняння 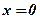є рівнянням осі ординат.

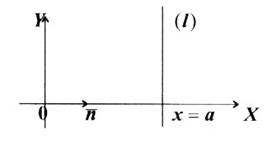
Рис.4

3.Аналогічно, при 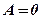рівняння записується 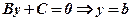, де 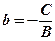. Вектор 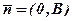належить осі 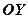. Пряма 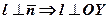в точці 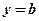(рис. 5) 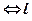||OX.

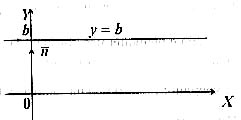
Рис.5.

Якщо ж 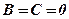, то 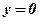– рівняння осі .

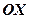Досліджене можна сформулювати в такій формі: пряма паралельна тій координатній осі, змінна якої в загальному рівнянні прямої відсутня.

Наприклад.

1) Пряма 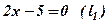. , доданок з 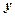– відсутній, тому .

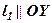2) Пряма 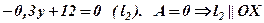.