Теоретичні відомості про градієнт функції

Похідна за даним напрямком . Градієнт функції.

Означення.Похідною функції z = f (x,y) в точці 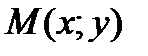за напрямком вектора

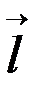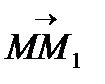= називається границя 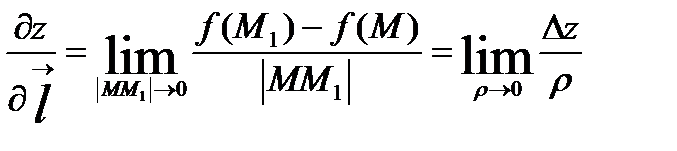, де .

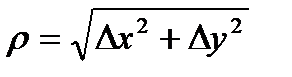Якщо функція f (x,y) диференційована, то похідна за даним напрямком визначається за формулою: 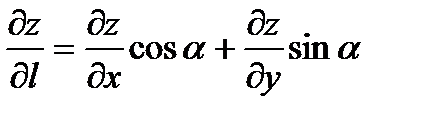, де 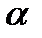- кут, утворений вектором 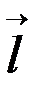з віссю .

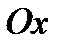Градієнтом функції z = f (x,y) в точці 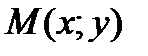називається вектор з початком в точці M, що має своїми координатами частинні похідні функції z:

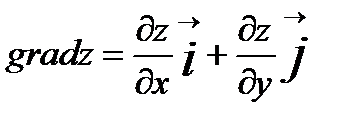. Градієнт функції і похідна за напрямком вектора 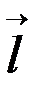пов’язані формулою: .

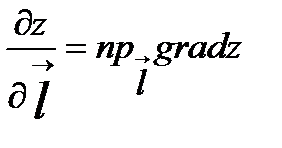Градієнт вказує напрям найшвидшого зростання функції в даній точці. Похідна 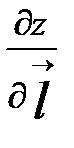за напрямком градієнта має найбільше значення , що дорівнює:

.

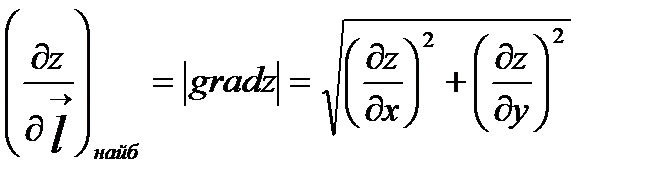Задача 3.Знайти похідну функції 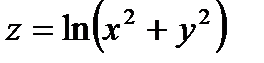в точці M(3;4)за напрямком градієнта функції z.

Задача 4. Мале підприємство виробляє товари А і В. Загальні щоденні витрати V (в гривнях) на виробництво xодиниць товару А та y одиниць товару В відомі: 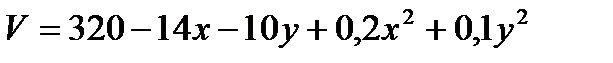. Визначити кількість одиниць товарів А і В, яку потрібно виробляти, щоб загальні витрати підприємства були мінімальними.

Питання для самоконтролю знань, умінь.

1. Означення функції двох змінних (трьох та більшого числа змінних).

2. Неперервність функції.

3. Частинні похідні функції двох змінних.

4. Частинні похідні другого порядку. Мішані частинні похідні.

1. Похідна функції за напрямком.
2. Градієнт функції двох змінних.

7. Правило дослідження функції двох змінних на екстремум.

Висновок __________________________________________________________

____________________________________________________________________

Перевірив викладач________Оцінка___________Дата_________

ТЕМА 6. ІНТЕГРАЛЬНЕ ЧИСЛЕННЯ

ПРАКТИЧНА РОБОТА № 13

Тема. Розв’язування задач на обчислення невизначених інтегралів частинами та заміною змінних

Мета роботи:Навчитись обчислювати невизначені інтеграли частинами та заміною змінних.

Наочне забезпечення та обладнання:

1. Інструкційні картки

2. Приклади задач

3. Роздаткові матеріали: опорні конспекти “Основні формули інтегрування”, “Властивості невизначеного інтегралу”.

4. Обчислювальні засоби: калькулятор.

Теоретичні відомості про невизначений інтеграл та методи інтегрування

Означення. Функція F(x) називається первісною для функції f(x), якщо f¢(x)=F(x).

Означення. Невизначеним інтегралом від функції f(x) називається сукупність усіх первісних цієї функції.

Використовується позначення 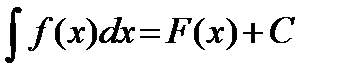,де f(x)dx - підінтегральний вираз, а C - стала інтегрування.

З геометричного погляду невизначений інтеграл – це сукупність (сім’я) ліній F(x)+C