Математикалық сөйлемдер

Мектеп математика курсында математикалық сөйлемнің мынадай түрлері кездеседі: аксиома; постулат; теорема; лемма; салдар.

Аксиома грекше axioma сөзінен алынған, оның сөздік мағынасы “ақиқатқа ие болған сөйлем”. Сондықтан да аксиомаға мектеп математика курсында мынадай анықтама берілген: “Дәлелдемесіз алынатын математикалық сөйлемдерді аксиома дейді”.

Аксиома негізінен ең қарапайым геометриялық фигура немесе қарапайым математикалық ережелердің негізгі қасиеттерін өрнектейтін сөйлем.

Мысал келтірейік: мектеп геометрия курсында қабылданған мынадай аксиомалар бар:

“Екі нүктені бастыра тек бір ғана түзу жүргізуге болады” және “Екі түзу тек бір ғана нүктеде қиылысады”. Бұл екі сөйлемнің екеуі де ақиқаттығы жағынан бірдей десек болады. Бірақ, бұл екеуін бірдей аксиомалар тізіміне енгізуге болмайды. Өйткені, егер бірінші сөйлемді аксиома етіп алсақ, онда оған сүйеніп екіншісін дәлелдеуге болады. Шынында да, егер екі түзу екі нүктеде қиылысады деп қарсы жорысақ, онда екі нүктені бастыра екі түзу жүргізуге болатын болып шығады. Ал бұл аксиома етіп алынған бірінші сөйлемге қайшы келеді. Сондықтан екі түзудің екі нүктеде қиылысуы мүмкін емес. Мұндай жағдайда екінші сөйлемді бірінші сөйлемнің салдары немесе екіншісі біріншісіне тәуелді дейміз. Мұнан аксиома етіп алынған сөйлемдер бір-біріне тәуелсіз болу керек деген қорытынды шығады.

Сонымен аксиомаларға қойылатын бірінші талаптың тұжырымдамасы – олар тәуелсіз болуы керек.

Аксиомаларға қойылатын екінші талап оларда қайшылық болмау керек.Мұны былай түсінеміз: Біріншіден, аксиомалар қатарына енгізілген сөйлемдердің ішінде бірінің ақиқаттаған пікірін жоққа шығаратын екінші аксиома болмау керек. Мысалы, “Берілген түзуден тыс жатқан нүктеден осы түзуге тек бір ғана параллель түзу жүргізуге болады” деген аксиомаға қосып, “берілген түзуден тыс жатқан нүкте арқылы осы түзуге параллель бірде-бір түзу жүргізуге болмайды” деген пікірді аксиома етіп алуға болмайды.

Аксиомаларға қойылатын үшінші талап – аксиомалар системасы толық болу керек.

Мұны былай түсінуге болады: егер аксиомалар системасы толық болмаса, онда оларға қосымша алғашқы аксиомаларға қайшы келмейтін және оларға тәуелсіз болатын аксиома қосуға болады, ал толық болса, онда жаңадан енгізілген аксиома не оларға тәуелді болады да, не оларға қайшы келеді.

Мектеп геометрия курсында төмендегі аксиомалар системасы бар:

1. Тиістілік аксиомасы:

а) Кез келген түзу сызық нүктелер жиынынан тұрады.

ә) Кез келген екі нүкте арқылы түзу жүргізуге болады және ол тек біреу ғана болады.

б) Қандай түзуді алсақ та, ол түзуге тиісті нүктелер де, оған тиісті емес нүктелер де бар болады.

2. Ара қашықтық аксиомасы:

а) Кез келген кесіндінің ұзындығы өзінің кез келген нүктесімен бөлінген бөліктері ұзындықтарының қосындысына тең болады. 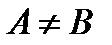болса, 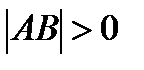, 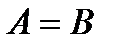болса, .

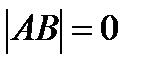б) А нүктеден В нүктеге дейінгі ара қашықтық В нүктеден А нүктеге дейінгі ара қашықтыққа тең: .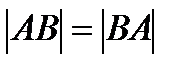

в) Кез келген үш А, В, С нүкте үшін А-дан С-ға дейінгі ара қашықтық А-дан В-ға және С-ға дейінгі ара қашықтықтардың қосындысынан артық емес: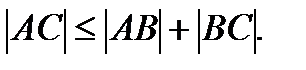

3. Реттілік аксиомасы:

а) Түзудегі үш нүктенің біреуі және тек қана біреуі қалған екеуінің арасында жатады.

б) Түзу жазықтықты екі жарты жазықтыққа бөледі.

Озғалыс аксиомасы.

а) Егер (АВ) ара қашықтық оң болып, ол (А₁ В₁) ара қашықтығына тең болса, онда А нүктесі А₁ нүктесіне және В нүктесін В₁ нүктесіне бейнелейтін тек бір ғана қозғалыс бар болады.

Параллельдік аксиомасы.

Берілген түзуде жатпайтын нүкте арқылы осы түзуге біреуден артық параллель түзу жүргізуге болмайды.

Постулат.

“Постулат” латын сөзі “талапты білдіруші” деген мағынаны білдіреді. Ол математикада аксиоманың синонимі ретінде қолданылады.

Кез келген ұғымды немесе ұғымдар арасындағы қатысты қанағаттандыратын талаптарды баяндайтын сөйлемді постулатдеп атайды.

Постулатқа мысалдар келтірейік:

1-мысал. Евклидтің “Негіздер” деп аталатын кітабында параллель аксиомасы “бесінші постулат” деп аталған. Кәдімгі белгілі математиктер осы параллельдік аксиоманы XIX ғасырдың бас кезіне дейін дәлелдеуге әрекет жасап келген. Бұл әрекет әрдайым нәтижесіз аяқталған. Параллельдік аксиоманың дұрыстығы ешкімге болса да шүбә келтірмесе де, оны белгілі бір аксиомалар мен ілгеріде бұрын дәлелденілген геометриялық сөйлемдердің салдары болып табылмас па екен деген сұрау барлық математиктерді қызықтырып келген. Параллель түзу сызықтар туралы бұл аксиоманы қарсы жору әдісін пайдаланып, яғни нүкте арқылы берілген түзу сызыққа параллель бірнеше түзу сызық жүргізуге болады деп есептеп дәлелдеуге әрекет жасаған математиктердің еңбегі де нәтижесіз болуы керек еді. Бірақ көрнекті орыс математигі Н.И.Лобачевский және оған хабарсыз венгер математигі Я.Бойяй нүкте арқылы берілген түзу сызыққа параллель бірнеше түзу жүргізуге болады, деген пікірді қабылдап, “Евклидтік емес” геометрияны құруға болатынын дәлелдейді. Лобачевский геометриясы сөйтіп дүниеге осылайша келді.

2-мысал. Эквиваленттік қатыс төмендегі үш постулат арқылы өрнектеледі:

1) арақатыс рефлексивті болуы керек: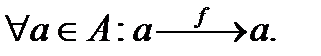

2) арақатыс симметриялы болуы керек:

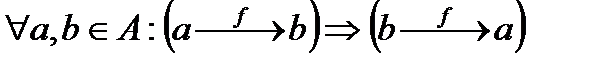
3) арақатыс транизитивті болуы керек:

;
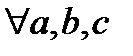
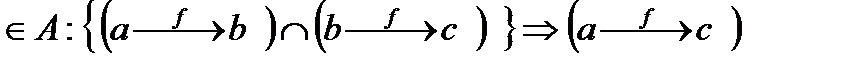