Формула Остроградского – Гаусса

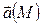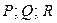Пусть в области G, ограниченной поверхностью σ, задано векторное поле . - единичный вектор внешней нормали к поверхности σ в точке М. Пусть функции и их частные производные непрерывны в замкнутой области G. Тогда справедлива формула Остроградского-Гаусса:

(22)

Поверхностный интеграл в правой части берётся по внешней стороне поверхности.

Или:

Векторная форма записи этой формулы: . (23)

Физический смысл формулы Остроградского-Гаусса: для того, чтобы поток векторного поля в сторону внешней нормали был отличен от нуля, внутри области G должны быть источники или стоки поля. Но тогда будет отлична от нуля. Само векторное поле как бы расходится от источников. Отсюда происходит название «дивергенция», или «расходимость».

Определение 11.Векторное поле 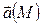называется соленоидальным в области G, если в каждой точке этой области .

Пример 18. Поле электрического точечного заряда е, помещённого в начало координат, описывается в точке 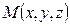вектором напряжённости 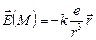, ( , 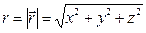.) Покажем, что поле соленоидально в каждой точке пространства 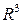,кроме начала координат.

Но

Аналогично: Тогда

( )= . Отсюда видим, что , если и , если , ч.т.д.

Из формулы Остроградского-Гаусса следует, что в объёмно односвязной области поток соленоидального поля через любую замкнутую поверхность, расположенную в этой области, равен нулю. Для объёмно неодносвязной области поток может и не быть равным нулю. Слово «соленоидальное» обозначает «трубчатое». Для соленоидального поля имеет место закон сохранения интенсивности векторной трубки, который заключается в следующем: в соленоидальном векторном поле 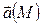поток через любое сечение векторной трубки имеет одно и то же значение. .

Векторные линии соленоидального поля не могут начинаться или заканчиваться внутри этого поля. Они начинаются и заканчиваются либо на границе области, либо являются замкнутыми кривыми. Так, векторные линии магнитного поля, создаваемого током, проходящим по проводнику, замкнуты.

Любое векторное поле можно представить суммой потенциального и соленоидального полей.

Пример 19.Найти дивергенцию векторного поля и исследовать расположение источников и стоков.

Решение. По формуле (21): .

, если .

Это уравнение цилиндра. Внутри цилиндра, в области - расположены стоки поля. Вне цилиндра, - расположены источники поля. На самом цилиндре нет ни источников, ни стоков.

Пример 20.Найти поток векторного поля через полную поверхность сферы .

Решение.

По формуле Остроградского – Гаусса (23): .

Вычислим . Тогда . Учитывая смещение сферы по оси OX, перейдём к сферическим координатам: , .

Тогда уравнение сферы примет вид: . Получим:

.

Ответ: .

Пример 21.Найти поток векторного поля через часть поверхности эллипсоида , в направлении, составляющем тупой угол с OZ, используя формулу Остроградского – Гаусса.

Решение. Рассмотрим замкнутое тело, ограниченное координатными плоскостями и заданной частью эллипсоида. Функции непрерывны вместе со своими частными производными во всех точках . Поток векторного поля через полную поверхность посчитаем по формуле (23)

, где , т.е.

. Перейдём к новым координатам: .

В этом случае эллипсоид преобразуется в сферу с уравнением . Имеем: .

С другой стороны, по свойству аддитивности поверхностного интеграла, поток П через замкнутую поверхность есть сумма потоков через часть эллипсоида, а также через части координатных плоскостей. Тогда: .

Потоки через части координатных плоскостей, замыкающих наше тело, посчитаем по формуле (18).

, т. к. ;

, т. к. ;

, т. к. .

Ответ: .

Данный пример иллюстрирует ещё один способ вычисления потока через часть поверхности – достраивание поверхности до замкнутого тела. Таким образом, мы получили три способа решения задачи нахождения потока векторного поля через часть поверхности :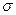

1) по формуле (13), определяющей понятие «поток»: 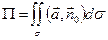, сводя задачу к вычислению поверхностного интеграла первого рода,

2) по формуле (18), как поверхностный интеграл второго рода,

3) по формуле Остроградского – Гаусса, «замыкая» поверхность и пользуясь понятием сложения потоков.

Контрольное задание 8.

1. Найти дивергенцию поля . Исследовать положение источников и стоков.

2. Найти поток векторного поля через полную поверхность тела, определяемого неравенствами: .

3. Найти поток векторного поля через полную поверхность тела, определяемого неравенствами: .

4. Найти поток векторного поля через полную поверхность тела, определяемого неравенствами: .

5. Вычислить поток векторного поля : а) через боковую поверхность конуса в направлении внешней нормали; б) через всю поверхность сферы в направлении внешней нормали.