Момент импульса относительно оси вращения для любого тела равен

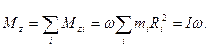(5.5)

В отличие от (5.4) эта формула выполняется для любого тела.

Тогда 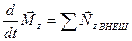. (5.6)

Подставив (5.5) в выражение (5.6), получаем 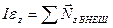, (5.7)

где 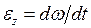- проекция углового ускорения на ось .

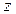Уравнение (5.7) аналогично второму закону Ньютона .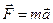

· Роль массы играет момент инерции,

· роль линейного ускорения - угловое ускорение,

· роль суммарной силы - суммарный момент внешних сил.

Поэтому (5.7) описывает динамику тела, вращающегося вокруг неподвижной оси, и называется основным уравнением динамики вращающегося тела.

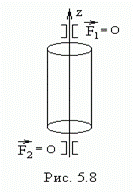
В случае вращения однородного симметричного тела(рис.5.8)

- силы бокового давления на подшипники не возникают.

- при отсутствии силы тяжести ось сохраняет свое положение в пространстве.

Ось, положение которой в пространстве остается неизменным при вращении вокруг неё тела в отсутствие внешних сил, называется свободной осью тела.

Для тела любой формы с произвольным распределением массы существуют три взаимно перпендикулярные, проходящие через центр масс тела оси, которые являются свободными осями. Они называются главными осями инерции тела.

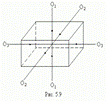
· У однородного параллелепипеда (рис.5.9) главными осями инерции являются оси 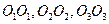, проходящие через центры противоположных граней.

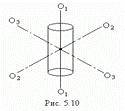· У тела, обладающего осевой симметрией, например, у цилиндра (рис.5.10) одной из главных осей является ось симметрии, две другие – любые две взаимно перпендикулярные оси, лежащие в плоскости, перпендикулярной к оси симметрии и проходящие через центр масс тела.

Таким образом, у тела с осевой симметрией фиксирована только одна из главных осей инерции.

У тела с центральной симметрией (шар) главными осями инерции являются любые три взаимно перпендикулярные оси, проходящие через центр масс, т.е. ни одна из главных осей не фиксирована.

Моменты инерции относительно главных осей называются главными моментами инерции тела.

В общем случае эти моменты различны: .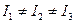

· Для тела с осевой симметрией два главных момента одинаковы, а третий от них отличен, 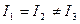. Такие тела называютсясимметричными волчками.

· У тел с центральной симметрией все три главных момента инерции одинаковы, эти тела называют шаровыми волчками.

Важной особенностью главных осей является то, что при вращении тела вокруг любой из них его момент импульса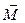

- совпадает по направлению с угловой скоростью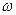

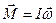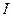- определяется как , где - момент инерции тела относительно данной главной оси (Заметим, что последнее соотношение справедливо и относительно осей, параллельных главным осям тела и не проходящих через его центр масс). Причем 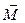не зависит от выбора точки, относительно которой его определяют (здесь предполагается, что ось вращения неподвижна).

Если твердое тело привести во вращение и затем предоставить самому себе, то направление оси вращения в пространстве, вообще говоря, будет меняться. Для того чтобы произвольная ось вращения тела сохраняла свое направление неизменным, к ей необходимо приложить определенные силы.

Рассмотрим этот вопрос более подробно на следующем примере.

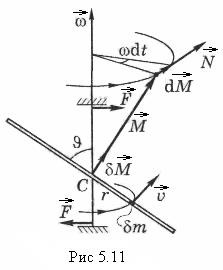
· Пусть середина С однородного стержня жестко скреплена с осью вращения так, что угол между стержнем и осью равен 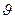(рис. 5. 11).

· Найдем момент 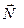внешних сил, которые необходимо приложить к оси вращения, чтобы при вращении стержня с угловой скоростью 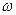ее направление не менялось.

Согласно основному уравнению динамики вращательного движения, .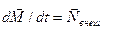

Таким образом, чтобы определить 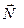, сначала надо найти момент импульса стержня 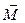, а затем его производную по времени.

Момент импульса 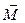проще всего определить относительно точки С.

Мысленно выделим элемент стержня массы 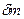, находящейся на расстоянии r от точки С.

Его момент импульса относительно этой точки 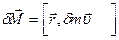,где 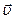- скорость элемента.

Легко видеть, что вектор 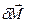направлен перпендикулярно стержню (рис. 5.11), причем его направление не зависит от выбора элемента 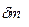. Поэтому суммарный момент импульса 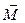стержня совпадает по направлению с вектором 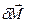. Заметим, что в данном случае вектор 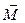не совпадает по направлению с вектором !

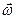При вращении стержня вектор 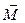будет также вращаться с угловой скоростью .

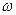За промежуток времени 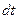вектор 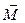получает приращение 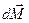, модуль которого, как видно из (рис. 5.11) равен

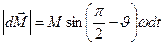, или в векторной форме .

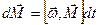Поделив обе части последнего выражения на 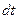, получим .

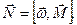Таким образом, действительно, для удержания оси вращения в неизменном направлении к ней необходимо в данном случае приложить момент 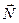некоторых внешних сил 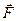(они показаны на рис. 5.11).

Однако нетрудно видеть, что если 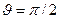, то вектор 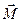совпадает по направлению с вектором 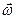, и в этом случае 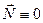, т. е. направление оси вращения будет оставаться неизменным без внешнего воздействия.

Наиболее просто убедиться в справедливости 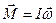можно для случая однородного тела с осевой симметрией.

Действительно, момент импульса твердого тела относительно оси вращения

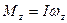
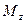( - проекция вектора 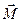, определенного относительно любой точки на этой оси). Но если тело симметрично относительно оси вращения, то из соображения симметрии сразу следует, что вектор 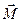совпадает по направлению с вектором 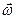и, значит, .

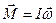В общем случае (ось вращения не совпадает ни с одной из главных осей, хотя и проходит через центр масс тела) направление вектора 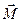не совпадает с вектором 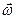, и связь между этими векторами носит сложный характер. Это обстоятельство является причиной сложного поведения вращающихся твердых тел.

Момент инерции

· Согласно формуле (5.2), момент инерции тела – аддитивная величина

,

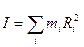момент инерции тела равен сумме моментов инерции всех его частиц.

· Момент инерции существует безотносительно к вращению. Каждое тело, независимо от того, вращается оно или нет, обладает определенным моментом инерции относительно любой оси.

· Из выражения (5.7) следует, что один и тот же момент силы вызывает большее угловое ускорение у того тела, у которого момент инерции меньше. Таким образом, момент инерции является мерой инертности тела при вращательном движении.

Эту формулу можно представить в виде ,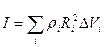

где 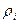- плотность 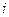-той частицы, 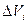- ее объем.

Если тело однородно, его плотность постоянна, и суммирование по всем частицам сводится к интегралу: 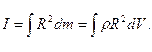Интегрирование производится по всему объему тела. Величины 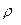и 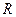зависят от местоположения частицы, т.е. являются функциями ее координат.

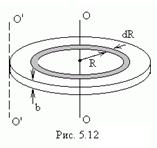пример: Найдем момент инерции однородного диска относительно оси, перпендикулярной плоскости диска и проходящей через его центр (рис. 5.12).

· Разобьем диск на кольцевые слои толщиной 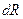и рассмотрим один такой слой.

· все его точки находятся на одинаковом расстоянии от оси вращения, равном 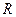. Объем слоя равен ,

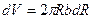где 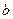- толщина диска.

· диск однородный, его плотность одинакова во всех точках, тогда момент инерции диска равен

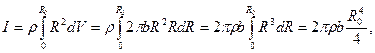
где 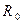- радиус диска.

· масса диска равна ,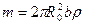

· получаем .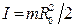

Определение момента инерции тела относительно произвольной оси существенно упрощается, если воспользоваться теоремой Штейнера: момент инерции 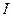относительно произвольной оси равен сумме момента инерции 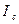относительно оси, параллельной данной и проходящей через центр масс тела, и произведения массы тела на квадрат расстояния 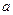между осями .

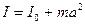Доказательство теоремы.

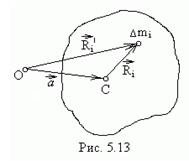
• Рассмотрим ось С (рис.5.13), проходящую через центр масс тела, и параллельную ей ось О, отстоящую от точки С на расстояние .
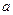• Из точки на оси О к оси С проведем вектор 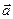,перпендикулярный к обеим осям.
• Из конца вектора 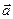проведем вектор 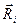, перпендикулярный к оси С в точку с элементарной массой .
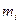• Аналогичный вектор 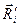проведем из начала вектора 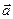к той же элементарной массе.
• Из рисунка видно, что
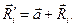
• Квадрат расстояния от оси С до выбранной частицы равен 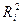, а от оси О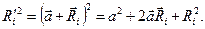
• Тогда момент инерции относительно оси О

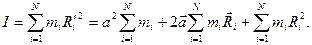где

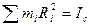- момент инерции тела относительно оси С,

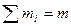- масса тела,

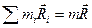, где 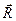- вектор, проведенный от оси С к центру масс тела, 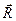=0, так как центр масс лежит на оси С, поэтому второе слагаемое равно нулю.

· Тогда получаем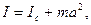

что и требовалось доказать.

В случае произвольного твердого тела связь между векторам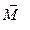и и 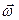более сложная, чем рассмотренная выше. Однако модули этих векторов всегда остаются пропорциональны друг другу, следовательно, каждая компонента вектора 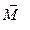будет линейно зависеть от компонент вектора :

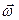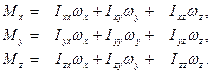
Здесь 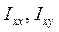и т.д. – коэффициенты пропорциональности, имеющие размерность момента инерции.

При увеличении 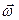в некоторое число раз в такое же число раз увеличится каждая из компонент 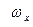, , 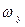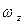и каждая из компонент 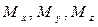, а значит, и сам вектор 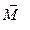. Взаимная ориентация векторов 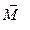и 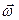определяется значениями коэффициентов пропорциональности. Все сказанное означает, что эти коэффициенты являются компонентами тензора второго ранга, который называется тензором инерции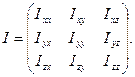

Гироскопы

Гироскопом называют массивное симметричное тело, вращающееся с большой угловой скоростью вокруг своей оси симметрии.

Рассмотрим поведение гироскопа на примере волчка.

Опыт показывает, что если ось вращающегося волчка наклонена к вертикали, то волчок не падает, а совершает так называемое прецессионноедвижение (прецессию)— его ось описывает конус вокруг вертикали с некоторой угловой скоростью 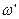, причем оказывается: чем больше угловая скорость и вращения волчка, тем меньше угловая скорость прецессии .

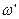Такое поведение волчка-гироскопа можно легко объяснить с помощью уравнения моментов (5.6), если только принять, что 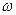>> 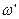(это условие, кстати, поясняет, что имеется в виду под большой угловой скоростью гироскопа).

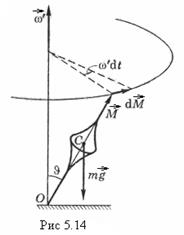Действительно, момент импульса 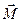прецессирующего волчка относительно точки опоры О (рис. 5.14) можно представить в виде суммы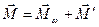

· момента импульса 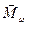, обусловленного вращением волчка вокруг своей оси,

· добавочного момента импульса 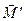, вызванного прецессией волчка вокруг вертикальной оси,

Поскольку ось волчка совпадает с одной из его главных осей,

то ,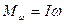

где 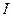- момент инерции волчка относительно этой оси.

Кроме того, ясно, что чем меньше угловая скорость прецессии, тем меньше и соответствующий момент .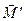

При 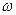>> 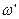во всех практически интересных случаях 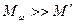, поэтому результирующий момент импульса 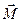почти совпадает с 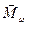как по модулю, так и по направлению, и можно считать, что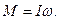

Зная поведение вектора 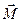, мы найдем и характер движения оси волчка-гироскопа.

Поведением вектора 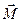управляет уравнение моментов .

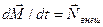Согласно ему, момент импульса 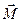относительно точки О (рис. 5.14) получает за время 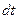приращение 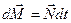, совпадающее по направлению с вектором 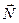— моментом внешних сил относительно той же точки О (в данном случае это момент силы тяжести m ).

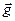Из рис. 5.14 видно, что .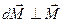

В результате вектор 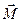(а следовательно, и ось волчка) будет поворачиваться вместе с вектором 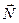вокруг вертикали, описывая круговой конус с углом полураствора 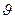. Волчок-гироскоп будет прецессировать вокруг вертикальной оси с некоторой угловой скоростью .

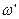Найдем связь между векторам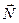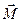и , и .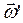

Согласно рисунку, модуль приращения вектора 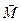за время есть

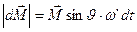, или в векторном виде .

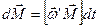Разделив на 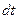, получаем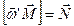

Из этого уравнения видно, что момент силы 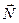определяет угловую скоростьпрецессии 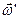(а не ускорение!). Поэтому мгновенное устранение момента 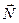приводит к мгновенному исчезновению и прецессии.

В этом отношении можно сказать, что прецессия не обладает инерцией.

Заметим, что момент сил 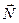, действующий на гироскоп, может иметь любую природу. Для обеспечения регулярной прецессии (постоянной угловой скорости 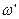) важно только, чтобы вектор 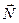, не меняясь по модулю, поворачивался вместе с осью гироскопа.

Пример. 1. Найдем угловую скорость прецессии наклонного волчка массы т, вращающегося с большой угловой скоростью 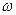вокруг своей оси симметрии, относительно которой момент инерции волчка равен 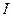. Центр масс волчка находится на расстоянии I от точки опоры.

Очевидно, ,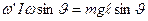

где 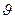— угол между вертикалью и осью волчка (рис. 5.14).

Отсюда .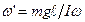

Интересно, что

· величина 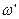не зависит от угла наклона 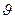оси волчка.

· полученный результат показывает, что 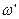обратно пропорциональна 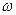, т. е., действительно, чем больше угловая скорость волчка, тем меньше угловая скорость его прецессии.

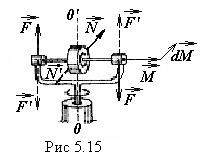Пример. 2. Рассмотрим эффект, возникающий при вынужденном вращении оси гироскопа. Пусть, например, ось гироскопа укреплена в U-образной подставке, которую мы будем поворачивать вокруг оси ОО' (рис. 5.15).

Если момент импульса 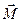гироскопа направлен вправо, то при таком повороте за время 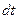вектор 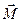получит приращение 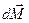- вектор, направленный за плоскость рисунка. Это означает, что на гироскоп действует момент сил 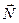, совпадающий по направлению с вектором .

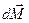Момент 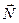обусловлен возникновением пары сил 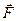, действующих на ось гироскопа со стороны подставки.

Ось же гироскопа в соответствии с третьим законом Ньютона будет действовать на подставку с силами 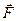' (рис. 5.15),

Эти силы называют гироскопическими; они создают гироскопический момент ' .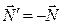

Заметим, что в данном случае гироскоп не обладает способностью противодействовать изменению направления его оси вращения.

Появление гироскопических сил называют гироскопическим эффектом.

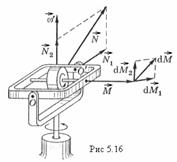Подобный гироскопический эффект, связанный, с возникновением гироскопического давления на подшипники, наблюдается, например, у роторов турбин на кораблях при поворотах и качке, у винтовых самолетов при виражах и т. п.

Проследим действие гироскопического момента на примере гироскопа, ось которого вместе с рамкой (рис. 5.16) может свободно поворачиваться вокруг горизонтальной оси ОО' U-образной подставки.

Если подставке сообщить вынужденное вращение вокруг вертикальной оси, как показано на рисунке вектором 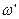, то момент импульса 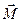гироскопа получит за время 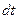приращение 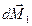— вектор, направленный за рисунок.

Это приращение обусловлено моментом 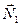пары сил, действующих на ось гироскопа 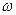стороны рамки. Гироскопические силы, действующие со стороны оси гироскопа на рамку, вызовут поворот последней вокруг горизонтальной оси ОО'. При этом вектор 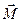получит дополнительное приращение 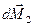, которое, в свою очередь, обусловлено моментом 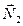пары сил, действующих на ось гироскопа со стороны рамки. В результате ось гироскопа будет поворачиваться так, что вектор 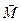будет стремиться совпасть по направлению с вектором .

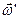Таким образом, за промежуток времени 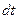момент импульса 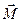гироскопа получает приращение .

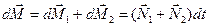При этом на рамку действует гироскопический момент .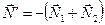

Составляющая этого момента 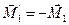вызывает поворот рамки вокруг горизонтальной оси ОО', другая составляющая 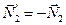противодействует повороту всей системы вокруг вертикальной оси (в отличие от предыдущего случая).

Гироскопический эффект лежит в основе разнообразных применений гироскопов: гирокомпас, гироскопический успокоитель качки корабля, гироскопический стабилизатор и др.