Дифференциалдық теңдеулер туралы жалпы түсінік.

Азақстан Республикасының білім және ғылым министрлігі

А. Байтұрсынов атындағы Қостанай мемлекеттік университеті

Математика кафедрасы

Ж.Даулетбаева

ДИФФЕРЕНЦИАЛДЫҚ ТЕҢДЕУЛЕР

Дістемелік көмекші құрал

050601-Математика, 050602-Информатика мамандығының

Студенттеріне

Останай, 2010

ББК........

Д19

Құрастырушы:Даулетбаева Жеміскүл Жүсіпбекқызы, математика кафедрасының аға оқытушысы

Рецензенттер:

Қасымханұлы Б., Қостанай мемлекеттік педагогикалық институтының доценті, ф.-м. ғ. к.

Беркімбай Р., математика кафедрасының аға оқытушысы

Ысмағұл Р., математика кафедрасының доценті, ф.-м. ғ. к.

Даулетбаева Ж.Д.

Д19 Дифференциалдық теңдеулер. Әдістемелік көмекші құрал.-Қостанай:

А. Байтұрсынов атындағы ҚМУ, 2009.- 76 б.

Әдістемелік көмекші құрал- университеттердің бағдарламасына сәйкестендіріліп жазылған.

Әдістемелік көмекші құрал университеттердің математика және қолданбалы математика мамандықтарында оқитын студенттерге, сондай-ақ математика саласы бойынша жас мамандар үшін бірден-бір құнды құрал болып табылады.

050601-Математика, 050602-Информатика мамандығы бойынша оқитын студенттерге арналған.

ББК........

Ақпараттық технологиялар факультетінің әдістемелік кеңесінде бекітілген, __.___ 200 ж. №__ хаттама

©А.Байтұрсынов атындағы Қостанай

мемлекеттік университеті

Мазмұны

Алғы сөз..............................................................................................................4

1 Дифференциалдық теңдеулер туралы жалпы түсінік.................................6

2 Бірінші ретті дифференциалдық теңдеулер................................................10

2.1 Айнымалылары ажыратылатын теңдеулер..............................................11

2.2 Біртекті дифференциалдық теңдеулер......................................................13

2.3 Біртектіге келтірілетін дифференциалдық теңдеулер............................. 14

2.4 Бірінші ретті сызықтық дифференциалдық теңдеулер............................18

2.5 Бернулли теңдеуі.........................................................................................21

2.6 Толық дифференциалдық теңдеулер.........................................................23

2.7 Туындылары арқылы шешілмеген бірінші ретті......................................26

дифференциалдық теңдеулер.....................................................................26

2.7.1 Толымсыз дифференциалдық теңдеулер...............................................26

2.7.2 Лагранж және Клеро теңдеулері.............................................................27

3 Жоғарғы ретті дифференциалдық теңдеулер..............................................29

3.1 Кейбір реті төмендетілетін дифференциалдық теңдеулер......................29

3.2 Жоғарғы ретті сызықтық дифференциалдық теңдеулер..........................32

3.3 Жоғарғы ретті тұрақты коэффицентті біртекті сызықтық теңдеулер.....34

3.4 Екінші ретті тұрақты коэффициентті біртекті сызықтық теңдеулер......36

3.5 Жоғарғы ретті тұрақты коэффициентті біртекті ......................................37

емес сызықтық теңдеулер............................................................................37

4 Жәй дифференциалдық теңдеулер жүйесі ...................................................44

4.1 Жәй дифференциалдық теңдеулер жүйелері. Жүйенің ...........................44

нормальдық қалпы.........................................................................................

4.2 Тұрақты коэффициентті сызықтық дифференциалдық ...........................45

теңдеулер жүйесі ...............................................................................................45

5 Дифференциалдық теңдеулер шешімдерінің орнықтылығы......................48

6 Дербес туындылы дифференциалдық теңдеулер........................................49

6.1 дербес туындылы теңдеулер. Сипаттауыштар. Коши есебі....................49

Қосымшалар.......................................................................................................54

Пайдаланылған әдебиеттер тізімі ...................................................................64

Алғы сөз

Əдістемелік көмекші құрал кредиттік технология бойынша жоғарғы оқу орнының математика, физика, информатика мамандықтары үшін, сондай-ақ экономикалық жəне техникалық мамандықтағы ішкі жəне сыртқы, сондай – ақ өздік оқу формасына даярланған.

Дифференциалдық теңдеулер тарауын жақсы игерту, оларды шешу əдістерін жетік білдіру мақсатында теориялық бөлімінен анықтамалар, теоремалар, формулалар енгізіліп, типтік тапсырмалардың шешу үлгілері талқыланады. Соңында өздік орындау жұмыстарына арналған жеке тапсырмалар нұсқалары ұсынылады. Олардың жеткілікті сан мөлшері осы əдістемелік құралды практикалық сабақтарда жаттығулар жинағы ретінде қолдануға мүмкіндік береді. Аталған мамандықтарда оқитын əрбір студент белгілі бір процестерді тану, оны игеру барысында айнымалылар арасындағы функционалдық тəуелділіктің аналитикалық мəнімен жиі кездеседі. Сондай-ақ, айнымалылар арасындағы байланысты іздеуге арналған көпшілік есептер белгісіз функциялардың туындысы немесе дифференциалы қатыстырылған теңдеулерді шешуге əкеледі.

Дифференциалдық теңдеулер тарауы туынды жəне интегралдар тарауымен тығыз байланысты болғандықтан осы тараулардың əрбір элементін жетік білу қажеттілігі туындайтынын ескерте кеткен жөн.

Дифференциалдық теңдеулер туралы жалпы түсінік.

y’ туындысы интегралдық қисыққа жүргізілген жанаманың бұрыштық коэффициенті болады.

Интегралдық қисықтың кез келген А(х, у) нүктесіндегі жанаманың бұрыштық коэффициентін дифференциалдық теңдеуді шешпей-ақ табуға болады.

Жанама интегралдық қисықтың бағытын көрсететін болғандықтан, f(x, y) функциясы үзіліссіз болса А нүктесін үзіліссіз жылжыта отырып, дифференциалдық теңдеуді интегралдау нәтижесінде алынатын қисықтардың бағыттар өрісін көрсетуге болады. Олар теңдеудің жалпы шешімі болады.

Анықтама. Қарастырылып отырған облыстың әрбір нүктесіндегіжанамалар жиынтығы бағыттар өрісі депаталады.

Жоғарыда айтылғандарды ескере отырып, дифференциалдық теңдеуді геометриялық тұрғыдан талқылайық:

1) Бірінші ретті дифференциалдық теңдеу берілді деген сөз - бағыттар өрісі берілген

2) Дифференциалдық теңдеу шешу не интегралдау дегеніміз - әрбір нүктесіндегі жанамалардың бағыты бағыттар өрісімен беттесетін барлық қисықтарды табу.

Анықтама. Бағыттар өрісінде көлбеулері бірдей қисықтар изоклиндердеп аталады.

Анықтама. Бір немесе бірнеше айнымалы функцияны, тәуелсіз айнымалыларды жəне функцияның туындыларын байланыстыратын теңдеу дифференциалдық теңдеудеп аталады.

Анықтама. Егер ізделінді функция тек бір ғана айнымалыдан тəуелді болса, онда дифференциалдық теңдеу қарапайым деп аталады.

Анықтама.Егер теңдеу бірнеше айнымалыдан тəуелді болып жəне оның осы айнымалылары бойынша алынған дербес туындылардан тұрса, онда дербес туындылыдифференциалдық теңдеу делінеді.

Біз тек қарапайым дифференциалдық теңдеулерді қарастырамыз.

Анықтама. Теңдеудің құрамындағы ең жоғарғы туындының реті дифференциалдық теңдеудің реті деп аталады.

G(x,y,y ′,y′′..., y^(п)) = 0 - n-ші ретті дифференциалдық теңдеу десек,

y^(п) = F(x,y,y′, y′′,y′′′,...) - бас туындыға қатысты шешілген теңдеу.

Мысалы. у′′+5xу′-x²y³= 0 – екінші ретті,

d³y/dx³–xy² dy/dx =7 - үшінші ретті,

y′+5xy = cosx – бірінші ретті дифференциалдық теңдеулер.

Анықтама.Дифференциалдық теңдеудің шешімі немесе интегралыдеп теңдеуге қойғанда оны тура теңдікке айналдыратын кез келген 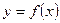функциясын айтады.

Мысал 1. y=sinx функциясы y′′+y=0 теңдеуінің шешімі.

Шынында, берілген теңдеудегі у белгілі, демек у′′-ті анықтайық:

у′ =cosx , у′′= - sinx

Егер y′′, y-ті теңдікке қойсақ: -sinx + sinx =0, яғни 0=0 теңдігіне келдік, демек у= sinx берілген теңдеудің шешімі болады.

Мысал 2. y= x²(1+Ce ^1/х) функциясы берілсін, мұндағы С – кез келген тұрақты сан. y функциясы х²у′+(1-2х)у= х² - бірінші ретті дифференциалдық теңдеуінің шешімі болатынын тексерелік.

Ол үшін берілген функцияның бірінші ретті туындысын табайық:

y′= 2x (1+С e ^1/x) +x² (0+С e ^1/х(- 1/x²))=2x(1+С e ^1/х)-Ce ^1/х

у пен у′-ті берілген теңдіктің сол жақ бөлігіне қойсақ:

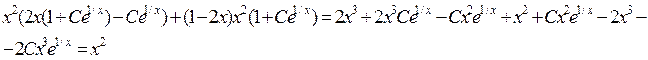
x²=x² тепе-теңдігіне келеміз, яғни берілген функция дифференциалдық теңдеудің шешімі.

Анықтама. Дифференциалдық теңдеудің шешімін анықтау дифференциалдық теңдеуді интегралдау есебі деп аталады.

Анықтама. Егер дифференциалдық теңдеудің шешімі, саны теңдеудің ретіне сəйкес келетін тəуелсіз кез келген тұрақтылардан тұрса, онда ол берілген теңдеудің жалпы шешімі деп аталады.

Мысалы, y= φ (х,С₁, С₂,..., С_n) n-ші ретті дифференциалдық теңдеудің шешімі.

Жалпы интегралдағы С₁, С₂,..., С_n тұрақтыларының орнына мəндер қойып дара шешімдер алуға болады.

Мысалы, 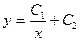функциясы xy'' +2y' =0- екінші ретті дифференциалдық теңдеудің жалпы шешімі болатынын тексерелік.

Шешуі: y ' , y '' - терді тауып теңдікке қоялық:

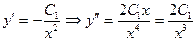
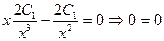, яғнитеңдеуді қанағаттандырады.

Жалпы шешімдегі С₁, С₂ тұрақтыларға мәндер беріп, дара шешімдер алуға болады: С₁=1, С₂=0 болғанда ,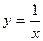

С₁= -3, С₂ =5 болғанда ,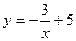

С₁=0, С₂=-1 болғанда .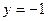

Анықтама. n-ші ретті дифференциалдық теңдеудің 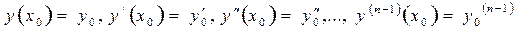- бастапқы деп аталатын шарттарды қанағаттандыратын дара шешімін табу Коши есебі (Огюстен Луи Коши (1789-1857) - француз математигі) деп аталады.

Берілген бастапқы n шартта 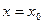аргументтің берілген мәніне сәйкес 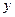функциясының және оның y ' , y '' ,..., y ⁿ⁻¹ туындыларының мәні беріледі. Сол шарттардың көмегімен 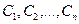тұрақтылардың сәйкес мәндері анықталады.