Детерминированные и ограниченно детерминированные функции.

Ограниченно-детерминированные функции, их также называют автоматами, моделируют дискретные преобразователи с памятью. В дискретные моменты времени на входы преобразователя поступают сигналы, в эти же моменты времени формируются выходные сигналы, которые зависят от всей информации, накопившейся в преобразователе, то есть от его «памяти».

Введем необходимые понятия и обозначения. Через 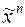обозначим конечный набор 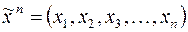, через 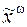– бесконечную последовательность: 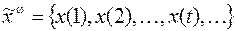, где каждое 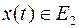, в частности, 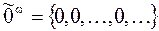, 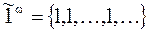. Набор последовательностей обозначим ,

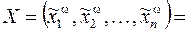
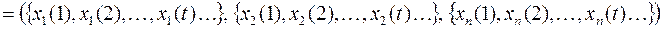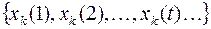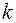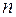Здесь последовательность можно рассматривать как последовательность сигналов, поступающих на – тый вход. можно рассматривать также как последовательность наборов сигналов, поступающих на входов преобразователя в дискретные моменты времени

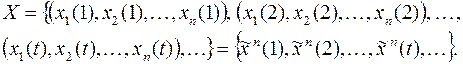
(в круглых скобках стоят конечные наборы, в фигурных – бесконечные последовательности). Оба вида представления: набор последовательностей или последовательность наборов равноправны.

Будем рассматривать функцию 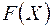, перерабатывающую вход

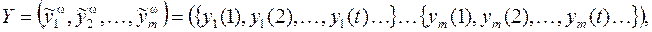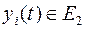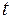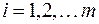где для любого момента времени и , а 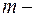число выходов у дискретного преобразователя. Выходные сигналя 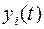и 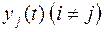не зависят друг от друга для любого момента времени 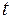, поэтому для простоты записи можно рассматривать преобразователь с одним выходом и с одной выходной последовательностью .

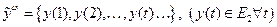Определение.

Функция 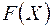называется детерминированной, если для любого момента времени 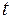и для любых входных последовательностей и таких, что 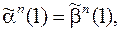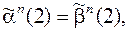…, 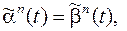формирующиеся выходные последовательности 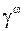и будут таковы, что … .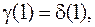

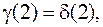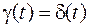Пример 1. Пусть 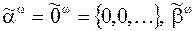– любая последователь-ность, отличная от постоянной 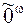. Зададим функцию 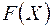следующим образом: 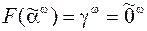, 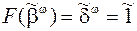. Такая функция, очевидно, не будет детерминированной. Рассмотрим 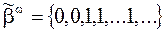, тогда 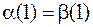, , 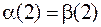но 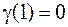, , 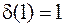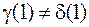аналогично, , .

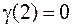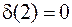Дискретные преобразователи формируют выходной сигнал в момент 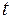в зависимости от сигналов, поступивших в моменты времени 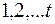, то есть реализуют детерминированную функцию.

Из определения детерминированной функции следует, что

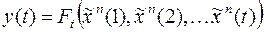для любого момента 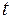, поэтому 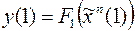, где 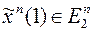, , 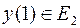следовательно, 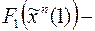булева функция и

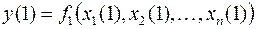
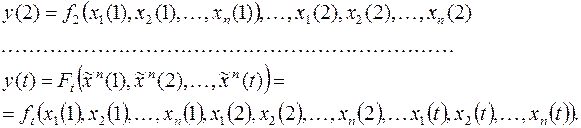
Таким образом, детерминированная функция 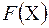есть последовательность функций алгебры логики. Множество всех детерминированных функций обозначим 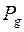. Если булевы функции задавались таблицей истинности, то детерминированную функцию можно задать с помощью информативного дерева.

Пусть 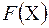– функция из 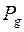. Рассмотрим бесконечное корневое ориентированное дерево, представленное на рис. 1.

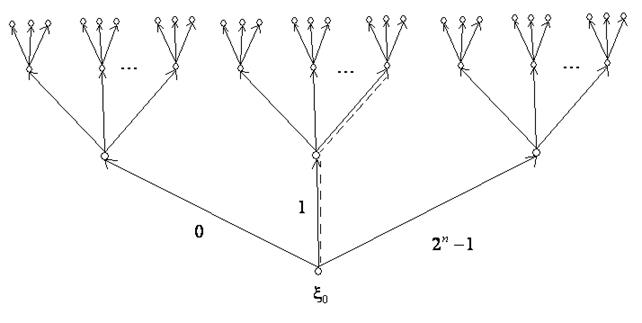Рис.1

Из корня этого дерева исходит пучок из дуг, образующих первый ярус. Каждая из дуг первого яруса ведет в вершину, из которой в свою очередь исходит пучок из 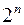дуг, образующих 2-й ярус, и т.д. Вершины, являющиеся концами дуг 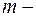го яруса, причисляются также к 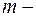ярусу. Вершина 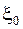считается вершиной нулевого яруса. Дуги каждого пучка нумеруются слева направо числами 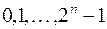, или их двоичными кодами длины .

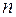Бесконечный простой путь с началом в корне 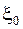будем называть ветвью рассматриваемого дерева. Очевидно, что каждой ветки дерева можно сопоставить последовательность 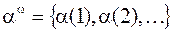входящих в эту ветвь, если идти по ней, начиная от коря. И наоборот, любой бесконечной последовательности чисел из множества 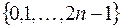однозначно соответствует некоторая ветвь дерева. Таким образом, существует взаимно-однозначное соответствие между множеством всех ветвей дерева и множеством всех бесконечных последовательностей чисел из множества 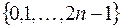, которые мы естественным образом можем занумеровать наборами из нулей и единиц длины .

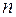Полученное дерево позволяет задать множество 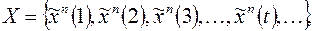область определения функции 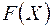, каждой ветви дерева соответствует последовательность входных наборов 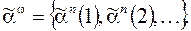На рис. 1. пунктиром выделена последовательность , , .

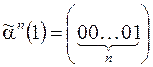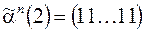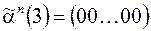Возьмем произвольную дугу 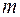-го яруса и рассмотрим путь, ведущий из корня дерева к этой дуге. Он определяется однозначно и характеризуется набором 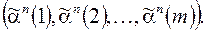Припишем выделенной дуге число 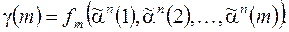Полученное дерево называется занумерованным деревом и является «аналогом» таблицы истинности для функции алгебры логики.

Таким образом, имея произвольную детерминированную функцию, можно построить соответствующее ей занумерованное дерево. С другой стороны, возьмем бесконечное ориентированное дерево с корнем, из каждой вершины которого исходят ровно 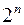дуг. Занумеруем его произвольным образом, т.е. каждой дуге припишем либо 0, либо 1. Ясно, что полученное занумерованное дерево определит, причем однозначным образом, некоторую детерминированную функции., зависящую от переменных .

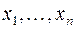Пусть 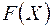– произвольная детерминированная функция. Рассмотрим соответствующее ей занумерованное дерево. Пусть 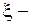произвольная его вершина из 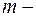го яруса. В нее ведет из коня 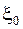путь 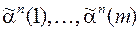. Совокупность всех ветвей, исходящих из 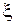, порождает некоторое дерево с корнем 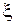(являющееся поддеревом исходного дерева). Так как исходное дерево занумеровано, то поддерево с корнем 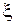также является занумерованным. Если в этом поддереве ввести свою нумерацию ярусов, начиная с первого, то поддереву будет соответствовать детерминированная функция 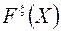. Каким образом связаны функци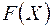и и ?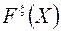

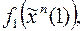
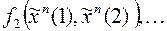
Пусть 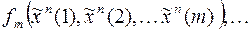– последовательность булевых функций, задающая детерминированную функцию 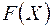; 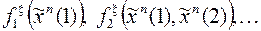– последовательность функций, задающая 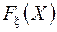, тогда для любого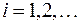

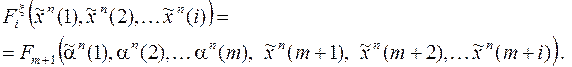
Два поддерева занумерованного дерева с корням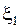и и 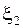называются эквивалентными, если

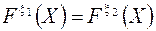
Пример 2. Рассмотрим сложение в двоичной системе двух последовательностей:

+

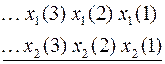
Построим корневое дерево. Из каждой вершины должно выходить 4 дуги с номерами 0,1,2,3, которые соответствуют входным наборам (00), (01), (11). Дуги всегда нумеруются слева направо, поэтому чтобы не загромождать чертеж, их нумерацию часто опускают, приписывая дугам только значение выходной последовательности.

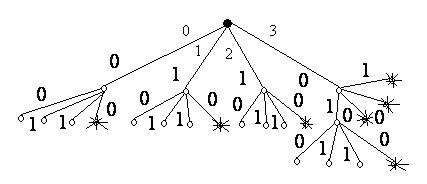Рис. 2.

На рис. 2 занумерованы дуги только первого яруса.

Если 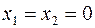, то 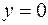, если 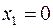, 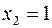или наоборот, то 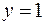, если 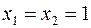, то 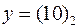, дуге с номером 3 приписан 0 и вершина помечена звездочкой, имея в виду, что 1 должна быть перенесена в старший разряд. Для дуг второго яруса, выходящих из этой помеченной вершины, значения функции будут отмечаться, при поступлении набора (00) 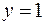, при поступлении наборов (01) , (10) или (11) опять будет происходить перенос в следующий разряд и соответствующие вершины помечены звездочкой. Очевидно, что деревья с непомеченными вершинами и деревья с помеченными вершинами порождают разные функции.

Отношение эквивалентности, введенное на множестве поддеревьев, позволяет разбить их на классы эквивалентности.

Число 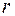классов эквивалентности, на которые разбивается множество поддеревьев, занумерованного дерева, называется весом дерева и соответственно, весом детерминированной функции.

Детерминированная функция называется ограниченно-детерминированной, или конечным автоматом, если она имеет конечный вес. Мы будем рассматривать только ограниченно-детерминированные функции, множество их обозначается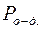

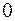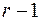Для обозначения классов эквивалентности занумерованного дерева вводят нумерацию вершин числами от до , где 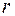- вес дерева.

Сначала занумеруем классы эквивалентности так, чтобы дерево, порожденное корнем, попало в класс с номером 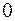. Далее, взяв произвольную вершину 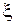, определяем, в какой класс эквивалентности попало дерево, порожденное этой вершиной. Пусть 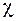- номер этого класса, тогда вершине 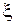припишем номер 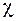. Занумерованное дерево вместе с занумерованными вершинами называют также информативным деревом.

Если дерево имеет конечный вес 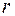, можно построить усеченное дерево – минимальное дерево, позволяющее восстановить все дерево (аналог периода). В усеченном дереве должно остаться по одной корневой вершине из каждого класса эквивалентности, и для каждой висячей вершины должно быть указано, какому классу эквивалентности она относится.

Пример 3. Дерево, приведенное на рис. 2, имеет вес 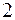. Отнесем вершины, помеченные звездочкой, к классу 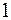, остальные – к классу 0. Построим для него усеченное дерево.

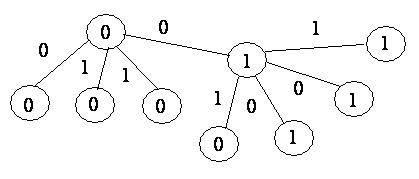Рис. 3.

Если в усеченном дереве склеить вершины с одинаковыми номерами, то получим диаграмму переходов или диаграмму Мура. Диаграмма Мура для усеченного дерева с рис. 3 приведена на рис. 4.

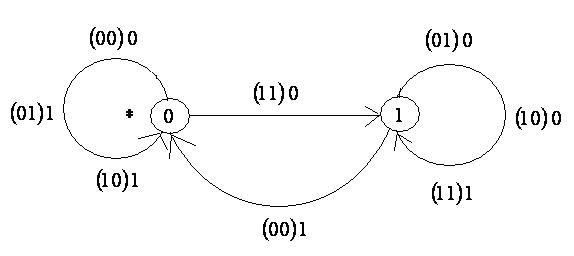Рис.4.

Класс эквивалентности, к которому относится корень дерева, помечают звездочкой. Каждой дуге приписано значение переменных 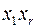, которое взято в скобке, и значение 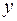. Если дуги кратные, их обычно не повторяют, наносят соответствующие значения 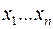и 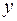на одну дугу.

Теорема (оценка числа ограниченно-детерминированных функций).

Число ограниченно-детерминированных функций веса 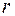, зависящих от 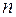переменных, не превосходит .

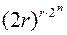Каждая о.-д. функция изображается диаграммой Мура и наоборот, по диаграмме о.-д. функция восстанавливается однозначным образом. Поэтому оценим число различных диаграмм. Диаграмма Мура – ориентированный граф, в котором 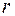вершин, из каждой вершины выходят 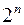дуг, всего 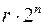дуг. Каждая дуга может зайти в любую из 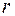вершин и каждой дуге приписано одно из двух чисел: 0 или 1, т.е. у каждой дуги 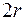возможностей, поэтому число различных диаграмм .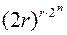