Далее - задачи о многоугольниках

Сумма углов многоугольника

Примечание. Данный материал содержит теорему и ее доказательство, а также ряд задач, иллюстрирующих применение теоремы о сумме углов выпуклого многоугольника на практических примерах.

Теорема о сумме углов выпуклого многоугольника

Для выпуклого n-угольника сумма углов равна 180°(n-2).

Доказательство.

Для доказательства теоремы о сумме углов выпуклого многоугольника воспользуемся уже доказанной теоремой о том, что сумма углов треугольника равна 180 градусам.

Пусть A 1 A 2... A n – данный выпуклый многоугольник, и n > 3. Проведем все диагонали многоугольника из вершины A 1. Они разбивают его на n – 2 треугольника: Δ A 1 A 2 A 3, Δ A 1 A 3 A 4, ... , Δ A 1 A n – 1 A n . Сумма углов многоугольника совпадает с суммой углов всех этих треугольников. Сумма углов каждого треугольника равна 180°, а число треугольников – ( n – 2). Поэтому сумма углов выпуклого n -угольника A 1 A 2... A n равна 180° ( n – 2).

Задача.

В выпуклом многоугольнике три угла по 80 градусов, а остальные - 150 градусов. Сколько углов в выпуклом многоугольнике?

Решение.

Для решения данной задачи воспользуемся теоремой о сумме углов выпуклого многоугольника.

Теорема гласит: Для выпуклого n-угольника сумма углов равна 180°(n-2).

Значит, для нашего случая:

180(n-2)=3*80+x*150, где

3 угла по 80 градусов нам даны по условию задачи, а количество остальных углов нам пока неизвестно, значит обозначим их количество как x.

Однако, из записи в левой части мы определили количество углов многоугольника как n, поскольку из них величины трех углов мы знаем по условию задачи, то очевидно, что x=n-3.

Таким образом уравнение будет выглядеть так:

180(n-2)=240+150(n-3)

Решаем полученное уравнение

180n - 360 = 240 + 150n - 450

180n - 150n = 240 + 360 - 450

30n = 150

n=5

Ответ: 5 вершин

Задача.

Какое количество вершин может иметь многоугольник, если величина каждого из углов менее 120 градусов?

Решение.

Для решения данной задачи воспользуемся теоремой о сумме углов выпуклого многоугольника.

Теорема гласит: Для выпуклого n-угольника сумма всех углов равна 180°(n-2).

Значит, для нашего случая необходимо сначала оценить граничные условия задачи. То есть, сделать допущение, что каждый из углов равен 120 градусам. Получаем:

180(n-2)=120n

180n - 360 = 120n

180n - 120n = 360 (это выражение рассмотрим отдельно ниже)

60n = 360

n=6

Исходя из полученного уравнения, делаем вывод: при величине углов менее 120 градусов, количество углов многоугольника менее шести.

Объяснение:

Исходя из выражения 180n - 120n = 360 , при условии, что вычитаемое правой части будет менее 120n, разность должна быть более 60n. Таким образом, частное от деления всегда будет менее шести.

Ответ: количество вершин многоугольника будет менее шести.

Задача

В многоугольнике три угла по 113 градусов, а остальные равны между собой и их градусная мера - целое число. Найти количество вершин многоугольника.

Решение.

Для решения данной задачи воспользуемся теоремой о сумме внешних углов выпуклого многоугольника.

Теорема гласит: Для выпуклого n-угольника сумма всех внешних углов равна 360°.

Таким образом,

3*(180-113)+(n-3)x=360

правая часть выражения - сумма внешних углов, в левой части сумма трех углов известна по условию, а градусная мера остальных (их количество, соответственно n-3, так как три угла известны) обозначена как x.

201+(n-3)x=360

(n-3)x=159

159 раскладывается только на два множителя 53 и 3, при чем 53 - простое число. То есть других пар множителей не существует.

Таким образом, n-3 = 3, n=6, то есть количество углов многоугольника - шесть.

Ответ: шесть углов

Задача

Докажите, что у выпуклого многоугольника может быть не более трех острых углов.

Решение

Как известно, сумма внешних углов выпуклого многоугольника равна 360⁰. Проведем доказательство от противного. Если у выпуклого многоугольника не менее четырех острых внутренних углов, следовательно среди его внешних углов не менее четырех тупых, откуда следует, что сумма всех внешних углов многоугольника больше 4*90⁰ = 360⁰. Имеем противоречие. Утверждение доказано.

Правильный многоугольник

Задача.
Найдите количество сторон правильного многоугольника,центральный угол которого равен:
1)120°
2)60°
3)72°

Решение.
Центральный угол - это угол, образованный двумя радиусами.

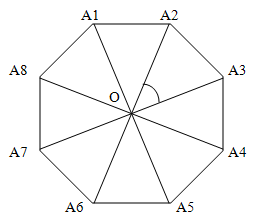
Так как многоугольник является правильным, все его стороны равны и все треугольники, которые образованы центром многоугольника и его углами - равны. Таким образом, все центральные углы также равны.

Общая мера суммы всех центральных углов равна 360 градусов.

Таким образом, количество сторон правильного многоугольника, исходя из градусной меры центрального угла будет равна:
1) 360 / 120 = 3 (правильный треугольник)
2) 360 / 60 = 6 (правильный шестиугольник)
3) 360 / 72 = 5 (правильный пятиугольник)

Ответ: 3; 6; 5 сторон.

Стереометрия

Куб

Примечание. Это часть урока с задачами по геометрии (раздел стереометрия, задачи о кубе). Если Вам необходимо решить задачу по геометрии, которой здесь нет - пишите об этом в форуме. В задачах вместо символа "квадратный корень" применяется функция sqrt(), в которой sqrt - символ квадратного корня, а в скобках указано подкоренное выражение. Для простых подкоренных выражений может использоваться знак "√".

Задача.
Площадь полной поверхности куба равна 24 см2. Найдите его объем.

Решение.
Поскольку куб имеет шесть одинаковых сторон, найдем площадь одной из них.

24 / 6 = 4 см²

Зная площадь стороны (основания) куба, найдем величину ребра

a = √4 = 2 см

Откуда его объем равен
S = a³ = 2³ = 8 см³ .

Ответ: 8 см³ .

Прямые и плоскости

Параллельные плоскости

Примечание. Это часть урока с задачами по геометрии (раздел плоскости). Если Вам необходимо решить задачу по геометрии, которой здесь нет - пишите об этом в форуме. В задачах вместо символа "квадратный корень" применяется функция sqrt(), в которой sqrt - символ квадратного корня, а в скобках указано подкоренное выражение. Для простых подкоренных выражений может использоваться знак "√"

Задача

Луч KM пересекает параллельные плоскости α и β в точках M₁ и М₂, а луч КР- в точках Р₁ и Р₂ соответственно. Вычислите длину отрезка М₁М₂ , если
КМ₁ = 8см.
М₁ Р₁ : М₂ Р₂ = 4 : 9

Решение.
Совершив геометрические построения, согласно условию задачи, увидим, что у нас образовались треугольники KM₁P₁ и KM₂P₂ .
У них общий угол K, а, поскольку плоскости α и β параллельны, то прямые М₁ Р₁ и М₂ Р₂ , лежащие на этих плоскостях, также параллельны. Поскольку параллельные прямые, пересекающие третью, образуют с ней равные углы, то треугольники KM₁P₁ и KM₂P₂ - подобны по трем углам. То есть имеют равные углы.

Поскольку треугольники KM₁P₁ и KM₂P₂ подобны, то
М₁ Р₁ / М₂ Р₂ = КМ₁ / KМ₂

Обозначим KМ₂ как х. Таким образом :
4 / 9 = 8 / x
4x = 72
x = 18

Ответ: 18 см

Задача

Через точку О, лежащую между параллельными плоскостями α и β, проведены прямые l и m. Прямая l пересекает плоскость A и B в точках А1и А2 соответственно, прямая m - в точках В1 и В2. Найти длину отрезка А2В2, если А1В1 = 12см, В1О:ОВ2 = 3:4

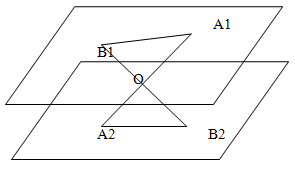
Решение.
Через прямые А1А2 и В1В2 можно повести плоскость, которая пересечёт параллельные плоскости по параллельным прямым А1В1 и А2В2.
У образовавшихся треугольников ОА1В1 и ОА2В2 соответствующие углы равны. Углы при вершине О равны как вертикальные, а остальные - как внутренние накрест лежащие у параллельных прямых. Следовательно треугольники ОА1В1 и ОА2В2 подобны.

У подобных треугольников соответствующие стороны соотностятся через коэффициент подобия.

Откуда:
ОВ1:ОВ2 = А1В1:А2В2,

Следовательно:
А2В2 = 4 * 12 / 3 = 16

Ответ: 16 см.

Параллельные плоскости (часть 2)

Примечание. Это часть урока с задачами по геометрии (раздел плоскости). Если Вам необходимо решить задачу по геометрии, которой здесь нет - пишите об этом в форуме. В задачах вместо символа "квадратный корень" применяется функция sqrt(), в которой sqrt - символ квадратного корня, а в скобках указано подкоренное выражение. Для простых подкоренных выражений может использоваться знак "√"

Задача

Через точку К, не лежащую между параллельными плоскостями альфа и бета, проведены прямые а и b. Прямая а пересекает плоскость альфа в точке А1 а плоскость бета в точке А2, и прямая b пересекает эти плоскости в точках B1 и B2 соответственно.
Найти KB2 если A2B2 относится к A1B1 как 4:3, а KB1 = 14 см.

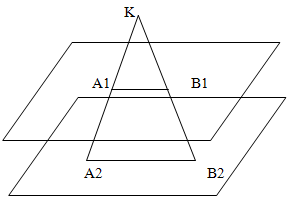
Решение.
Через прямые a и b проведем плоскость, образованную этими пересекающимися прямыми. В этой плоскости лежат треугольники A2KB2 и A1KB1. Эти треугольники подобны, так как угол К у них общий, а остальные углы также равны, так как образованы секущими KA2 и KB2 на параллельных прямых A1B1 и A2B2, так как плоскости альфа и бета - параллельны.

Таким образом, коэффициент подобия верен для соотношения любых двух соответствующих сторон, то есть:
KB2 : KB1 = 4:3

Откуда
KB2 : 14 = 4:3
KB2 = 14 * 4 / 3 = 56/3 = 18 2/3 см

Ответ: 18 2/3 см