Периодическая последовательность прямоугольных видеоимпульсов

Пусть определяет периодическую последовательность видеоимпульсов с амплитудой , длительностью и периодом .

рис. 1.3

Такая функция может быть описана как:

Переходя к спектральному представление, определяем коэффициенты разложения такого сигнала в ряд Фурье.

Здесь – скважность импульсов,

– коэффициент заполнения.

Амплитуда косинусных составляющих имеет вид:

где

Умножим и разделим на , тогда

Амплитуды синусных составляющих:

где

Таким образом,

Учитывая, что

Разложение сигнала можно записать несколько в иной форме:

Расчет спектра удобно вести в комплексной форме:

(1.24)

Отсюда приходим к комплексной форме ряда Фурье для исследуемого сигнала:

(1.25)

Анализ полученных выражений позволяет сделать следующие выводы:

1. Постоянная составляющая обратно пропорциональна скважности .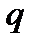

2. Амплитуды всех гармоник пропорциональны амплитуде импульсов и уменьшаются с ростом скважности .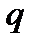

3. Амплитуды гармоник не зависят от сдвига импульсов во времени , а зависят лишь от длительности (скважности). С другой стороны начальные фазы гармоник зависят от амплитуды импульсов и их длительности, т.е. сдвиг сигнала во времени не влияет на его АЧС, а изменяет только ФЧС.

4. Распределение амплитуд гармоник по величине подчиняется закону: где .

Это определяет появление знака “+” или “-“, что соответствует изменению фазы гармоник на . Учитывая это можно записать:

где -номер интервала значений , при которых функция принимает отрицательные значения.

Во всех случаях начальная фаза гармоник определяется как

(1.26)

Особенности спектров можно сформулировать в общих чертах:

1. Спектральные лини находятся друг от друга на одинаковом расстоянии, равном частоте исследования импульсов .

2. Распределение спектральных линий по высоте определяется огибающей спектра, характер которой зависит от формы сигнала.