Функция неопределенности прямоугольного радиоимпульса

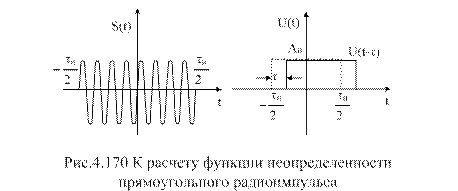
Сигнал представляет собой прямоугольный радиоимпульс с гармоническим заполнением (рис.4.170)

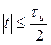. (4.95)

При вычислении функции неопределенности рассмотрим отдельно случаи положительных и отрицательных временных сдвигов между импульсами. При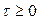

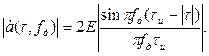
При 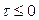результат аналогичен. Обобщая результаты получим

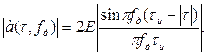(4.96)

Рассмотрим сечение функции неопределенности для случая f_д=0. Результат получится следующий

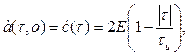
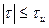. (4.97)

Сечение соответствующей поверхности плоскостью f_д=0 изображена на рис.4.171

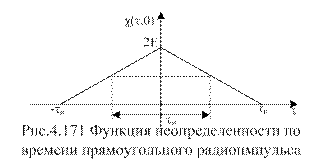
При сечении плоскостью τ=0 получаем

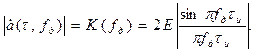(4.98)

Полученная формула соответствует модулю спектра прямоугольного видеоимпульса, являющего огибающей исходного сигнала (рис.4.172).

На рис.4.163 изображена диаграмма неопределенности прямоугольного радиоимпульса

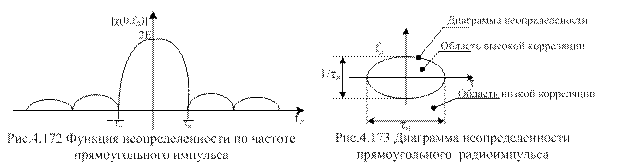
Чем больше длительность импульса, тем выше разрешающая способность по частоте, но хуже разрешающая способность по времени. Чем меньше длительность импульса, тем выше разрешающая способность по времени, но хуже по частоте. Такое положение является иллюстрацией принципа неопределенности в радиолокации.

Широкополосные сигналы

Импульсный сигнал считается широкополосным, если произведение его длительности на ширину спектра частот 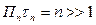. Есть и другой подход в определении широкополосности сигнала. Так, например, в 1990 в США введено общее определение относительной полосы частот η:

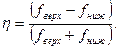
В соответствии с этим определением сигналы, имеющие полосу η≤0,01 относится к узкополосным; имеющие 0,01<η≤0,25 относится к широкополосным; имеющие 0,25<η<1 относятся к сверхширокополосным (СШП).

В качестве СШП могут использоваться кодоимпульсные последовательности, линейно-частотно-модулированные сигналы, псевдошумовые сигналы, видеоимпульсы, не имеющие высокочастотного заполнения и радиоимпульсы, имеющие высокочастотное заполнение, состоящее из нескольких периодов высокочастотного колебания. Внешний вид сигналов изображен на рис.4.174.

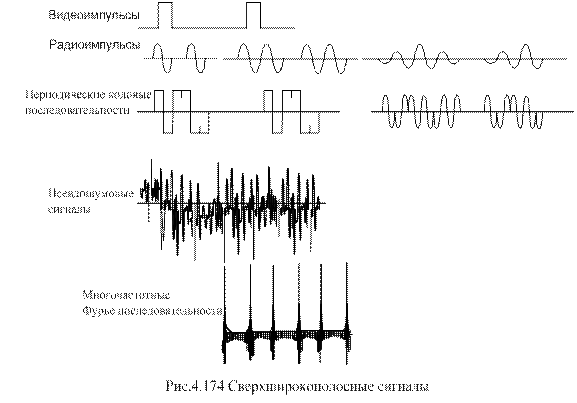
Широкополосность сигнала достигается путем внутриимпульсной модуляции фазы или частоты колебаний. Широкополосный сигнал (радиоимпульс) имеет ширину спектра в n раз большую, чем импульс той же длительности 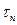без внутриимпульсной модуляции ширина его спектра соответствует импульсу без внутриимпульсной модуляции существенно меньшей длительности .

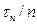Обработка широкополосных сигналов реализуется в оптимальных фильтрах, импульсы, на выходе которых определяются амплитудно-частотным спектром сигнала. Широкополосные радиоимпульсы в оптимальном фильтре сжимаются, причем тем сильнее, чем больше произведение 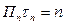.