Способы получения и методы обработки информации о параметрах движения цели

Информация о фазовых координатах цели: векторе дальности и ее относительных координатах может быть получена при непосредственном наблюдении цели или ее изображения, а также косвенным путем – путем вычислений, – через известные параметры движения БАК. Рассмотрим методы получения информации о фазовых координатах цели.

Для непосредственного наблюдения за целью или ее изображением используются различные визирные устройства, входящие в состав бортовых ОПС. Для косвенного определения используются системы счисления пути.

Одним из основных признаков классификации визирных устройств и систем является область (диапазон) спектра электромагнитных колебаний, в котором они работают. По этому признаку визирные системы можно разделить на две группы:

- визирные системы, работающие в оптическом диапазоне (длины волн от 10^-5 до 5×10^-4 м);

- визирные системы, работающие в радиодиапазоне (длины волн от 5×10^-4 до 10⁴ м).

Визирные устройства и системы оптического диапазона подразделяются на оптические и оптико-электронные. Последние могут быть пассивными или активными. В пассивных используется или собственное излучение цели, или отраженное целями излучение внешних источников, например, Солнца. В активных используется отраженная от цели энергия излучения, создаваемая источником в составе обзорно-прицельной системы.

Пассивные визирные системы подразделяются на:

- системы с электронно-оптическими преобразователями;

- оптико-телевизионные системы;

- тепловизионные системы.

К активным оптико-электронным системам относятся главным образом лазерные локаторы.

Основным недостатком визирных систем оптического диапазона является ограниченность их применения в сложных метеоусловиях. Этого недостатка лишены визирные системы, работающие в радиодиапазоне – бортовые радиолокационные станции.

РЛС могут быть активного и пассивного типа. В активных – информация о координатах и параметрах движения цели получаются на основе анализа зондирующих и отраженных сигналов. В пассивных – пеленгационных РЛС – используется излучение внешних источников, например, излучение работающих РЛС противника.

Недостатками радиолокационных систем являются их демаскирующее действие и подверженность воздействию средств радиоэлектронной борьбы и радиоэлектронного противодействия.

Визирные системы оптического и радиодиапазонов в зависимости от принципа действия и особенностей конструкции обеспечивают определение различных угловых координат цели относительно БАК. Такими координатами могут быть, например, бортовой угол визирования цели φ_y и угол места цели φ_z.

Возможно определение угловых координат относительно осей, стабилизированных по крену и тангажу. Пеленгационные и панорамные РЛС обеспечивают определение одного угла – пеленга (азимута) цели.

Колебания БАК относительно центра масс могут вызывать ошибки в определении угловых координат цели. Одним из основных способов уменьшения влияния колебаний является стабилизация системы отсчета. Стабилизация может быть осуществлена:

- путем стабилизации всех или отдельных устройств бортовой ОПС;

- путем коррекции положения визирной линии с помощью устройств управления визирной линией по соответствующим формульным зависимостям.

Первый способ называют геометрической, второй – аналитической стабилизацией системы отсчета.

Дальность до цели D измеряется дальномерами. Как и визирные системы, есть дальномеры оптического диапазона: оптические дальномеры с базой на цели и лазерные дальномеры, и радиодиапазона – радиодальномеры. Радиодальномеры обеспечивают определение не только дальности D, но и производной по времени .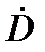

Как уже было указано ранее, для получения вектора дальности цели 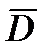при непосредственном наблюдении за целью (или ее изображением) требуется иметь модуль и два угла, определяющие орт 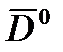вектора дальности. Визирные устройства (системы), как таковые, выдают информацию об орте 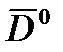, т.е. об угловых координатах цели. Определение модуля 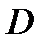обеспечивают дальномеры, которые обычно входят в состав ОПС. В этом случае ОПС обеспечивает определение вектора .

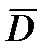Для косвенного определения вектора дальности 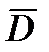до неподвижных НЦ может использоваться метод счисления пути. В основе метода лежит следующая формула:

,

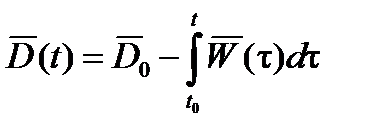где 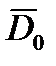– вектор начальной дальности цели.

Интеграл в правой части представляет путь, пройденный БАК за промежуток времени (t – t₀) относительно земли. Практически задача счисления пути может решаться в различных системах координат. При решении навигационной задачи для счисления используются сферические координаты, а при решении задачи прицеливания – прямоугольные.

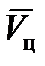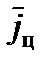Параметры движения цели и определяются по результатам наблюдения ее движения. В настоящее время нашли широкое применение два метода [14].

а) Непрерывное наблюдение цели

Первый метод состоит в определении параметров движения цели через производные по времени от вектора 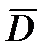, вектор 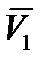, производную вектора 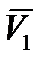или, что то же, через ускорение БАК. Определение производных вектора 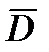может быть осуществлено при непрерывном наблюдении движения цели – сопровождении цели. Коротко этот метод будем называть методом непрерывного наблюдения за движением цели.

Второй метод состоит в определении параметров движения цели через векторы 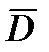, измеренные в дискретные моменты времени, и векторы перемещений БАК. Коротко этот метод будем называть методом дискретных наблюдений за движением цели.

Если применен первый метод, то

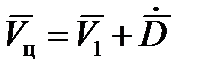. (20)

Дифференцируя выражение (20), получим:

,

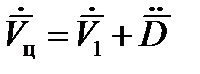или

.

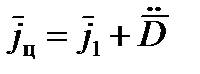Таким образом, требуется в процессе сопровождения цели получить данные, необходимые для определения векторов , , , .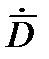

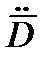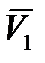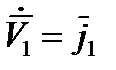Принципиально данный метод не требует делать какие-либо предположения о движении цели до отделения НАСП. Вместе с тем, практически измеренные величины для определения указанных выше векторов будут содержать ошибки. Необходима фильтрация этих ошибок. Требуемое время наблюдения за движением цели до отделения НАСП определяется из условия наилучшей фильтрации ошибок.

б) Дискретное наблюдение цели

Существо второго (дискретного) метода рассмотрим на примере определения вектора скорости цели 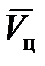. Предположим, что цель до отделения НАСП перемещается так, что ее вектор скорости остается постоянным. Рассмотрим следующую схему (рис. 13).

Пусть в момент времени 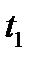определен вектор дальности 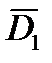до цели – выполнено первое наблюдение. Через некоторое время в момент 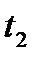определен вектор дальности 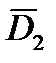– сделано второе наблюдение. Интервал времени 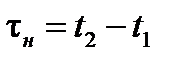. Из рассмотрения схемы следует:

,

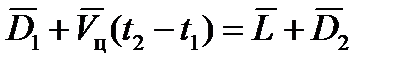откуда

.

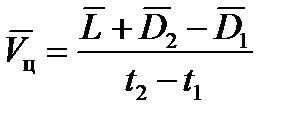Значит, для определения 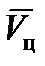необходимо знать 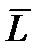, , 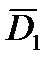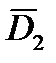и интервал времени 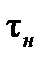. Если, например, 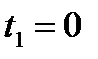, тогда интервал можно рассматривать как текущее время t. Вектор 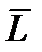можно определить путем счисления:

.

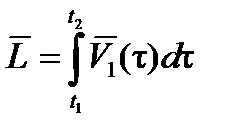Отметим главные особенности второго метода. При необходимости экстраполяции движения цели придется распространить гипотезу о постоянстве вектора 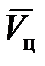и на промежуток времени экстраполяции 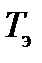. При большом времени наблюдения 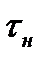и при отклонении реального движения цели от принятого по гипотезе могут возникнуть большие ошибки в определении 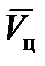, а значит, и в определении .

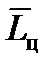При наличии ошибок в 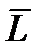, , 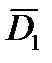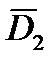их влияние на определение 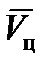сказывается тем меньше, чем больше 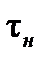, так как ошибки усредняются на интервале 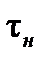. Однако, при большом 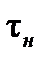, как указывалось, могут возникнуть большие ошибки в определении 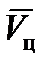в случае отклонения реального движения цели от принятого по гипотезе.

Для определения 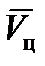требуется запоминание вектора 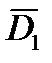и интервала 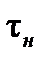, а также счисление 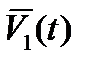в невращающейся системе координат.

С помощью второго метода можно определить и вектор ускорения цели 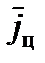, не прибегая к использованию производных 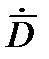и 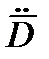. Чтобы получить не только 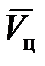, но и 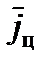, необходимо выполнить три наблюдения за движением цели. На рис. 14 приведена соответствующая схема.

Допустим, что на участке 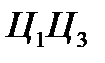до отделения НАСП цель движется с постоянным ускорением 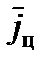. Тогда из рассмотрения схемы следует:

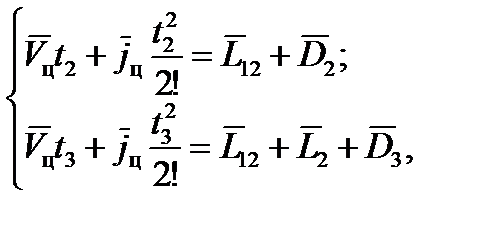(21)

где .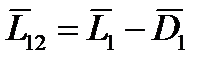

Решив систему (21), например, методом исключения неизвестных, получим следующие выражения для 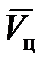и :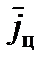

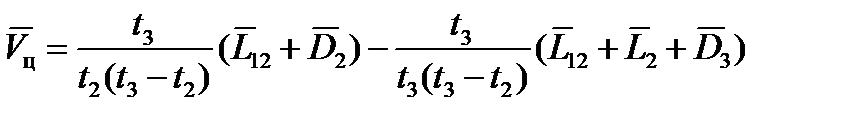; (22)

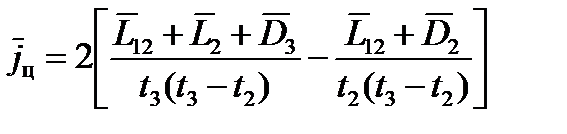. (23)

Входящие в формулы (22) и (23) величины нужно определять и запоминать, необходимо измерять 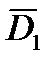, , 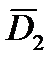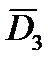и определять 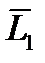и .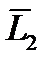

Получим скалярные выражения для параметров движения цели в случае применения первого метода. В соответствии с (20) необходимо определить производную вектора дальности 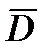. Для определения 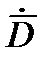может быть применена следующая формула:

,

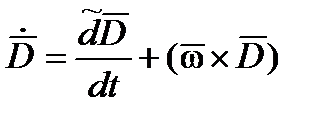где 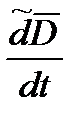– локальная производная вектора 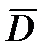, определенная при условии, что система координат, в которой задан вектор 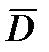, не вращается;

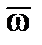– угловая скорость вращения указанной системы координат.

При выборе связанной с БАК системы координат выражение для 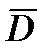в проекциях будет иметь следующий вид:

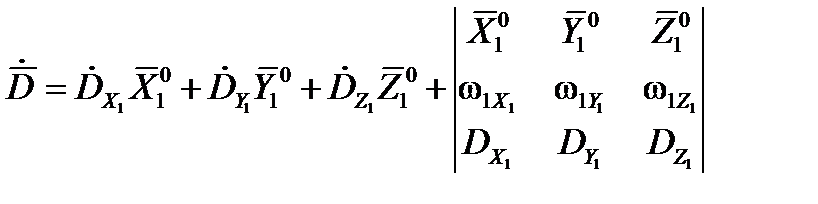. (24)

Тогда для проекций 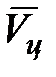в соответствии с (20) и (24) можно получить:

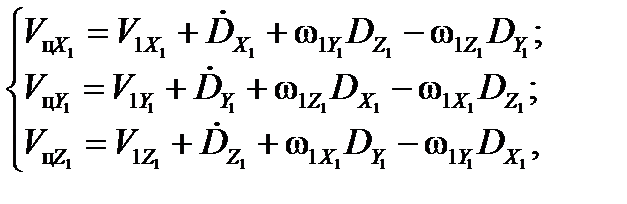
где 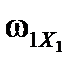, , 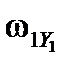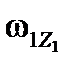– проекции вектора угловой скорости БАК 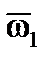на оси связанной с БАК системы координат.

При выборе лучевой системы координат 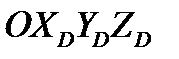, у которой ось 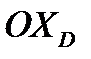направлена по вектору 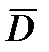, в формуле (24) необходимо положить:

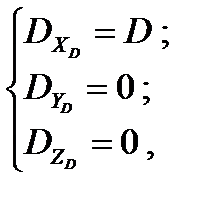
тогда для 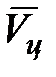на основе (20) можно получить:

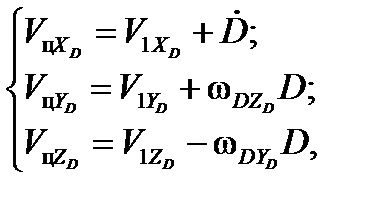
где 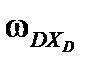, , 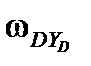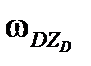– проекции вектора 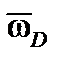вращения системы координат 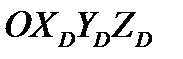относительно воздуха на оси этой системы.

Формулы для проекций 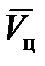на оси системы 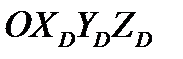имеют простейший вид. Поэтому на практике чаще всего используется эта система координат.

При выборе невращающейся системы 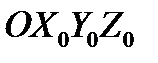в формулах (24) необходимо положить 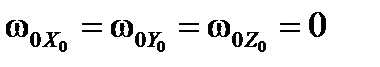. Тогда:

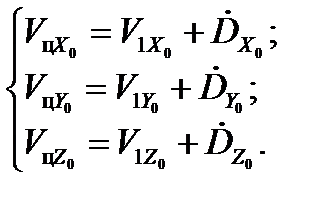
Как отмечалось выше, для определения параметров движения цели вторым методом необходимо воспользоваться системой координат 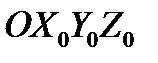. Для проекций вектора 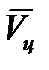в соответствии с (22) можно получить:

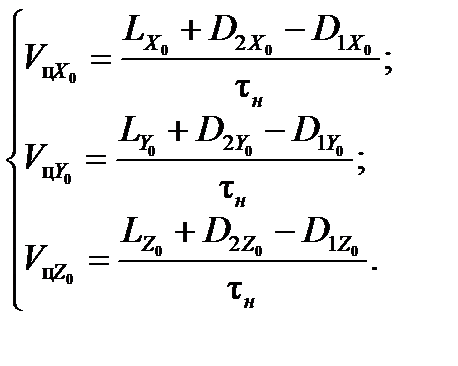(25)

Так как для определения проекций в (25) в качестве исходной информации будут использованы проекци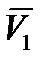и и 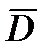в связанной с БАК системе координат, необходимо знать матрицу , (…).

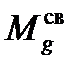Подводя итог изложенному об определении параметров движения цели, необходимо отметить следующее.

Определение проекций вектора 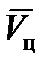в настоящее время в современных АПрС не вызывает особых трудностей. Имеющиеся бортовые средства информации и вычислительные устройства обеспечивают определение проекций 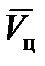с высокой степенью точности и надежности.

Важным преимуществом метода дискретных наблюдений за движением цели является возможность использования одной и той же информации как для определения проекций 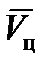, так и 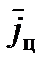. Достаточно определять с высокой точностью и надежностью координаты цели и перемещение БАК.

Для определения параметров движения цели требуются данные многих средств информации. В современных АПрС принимаются меры к уменьшению влияния колебаний БАК и ошибок в исходной информации на точность учета движения цели. С этой целью применяются различные методы фильтрации ошибок, сглаживания измеренных параметров и комплексной обработки данных от разных средств информации.