Методы построения графиков функций
Графики функций. Примеры построения.
График функции y=f(x) - это геометрический объект, который характеризуется тем, что каждая точка c координатами (x, y) этого геометрического объекта удовлеворяет уравнению y=f(x). Например, график синуса - это геометрическое место точек на плоскости, которые удовлетворяют уравнению y=sin(x). Ниже в этой статье мы рассмотрим графики основных элементарных функций, таких как:
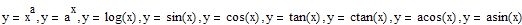
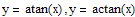
Это графики основных простейших функций:
а именно - график степенной функции,
график показательной функции,
логарифмической y=log(x),
синуса y=sin(x),
косинуса y=cos(x),
тангенса,
котангенса,
арксинуса,
арккосинуса,
арктангенса,
и арккотангеса.
Также мы займемся на этой странице исследованием и построением графика функции с помощью производной, (см. раздел Производная функции. Примеры решения). Мы будем находить промежутки возрастания и убывания, точки максимума и минимума, точки пересечения с осями координат, касательные к графику функции, а также асимптоты (горизонтальные, вертикальные, наклонные). Мы увидим, что для постоения асимптот необходимо будет уметь решать пределы функций. Также для построения графика понадобятся промежутки выпуклости/вогнутости, или что то же самое выпуклости вверх выпуклости вниз, а также точки перегиба. Точки перегиба графика определяются с помощью второй и старших производных.
Методы построения графиков функций
Существует три способа построения графиков функций:
1.Поточечный метод, который заключается в выборе нескольких точек на оси абсцисс, вычислении их ординат и откладывании соответсвующих значений по осям. Затем, согласно поточечному методу, строятся точки по вычисленным значениям ординат и отложенным значениям абсцисс и, соединяя эти точки плавной линией, получается график функции. Этот метод еще называют просто построением графика функции по точкам или по коодинатам.
Пример. Построим график параболы по точкам. Выберем например, точки
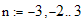
то есть мы взяли точки( или целые числа) от минус трех до трех. Будем строить график функции
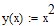
для этого мы должны взять сначала -3, отложить это число по оси икс влево, то есть влево надо отложить три единицы, возвести в квадрат тройку, получить девятку, отложить эту девятку по оси ординат вверх от точки минус три на оси абсцисс, получив первую точку графика параболы, затем аналогично строятся остальные пять точек графика и соединяются ломаной линией. Таким образом получается приближенная версия графика параболы
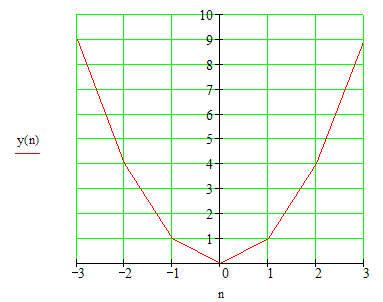
На самом деле парабола предсталяет собой гладкую плавную линию, получить которую или кривую более похожую на идеальную параболу, можно, взяв более густое множество точек на оси иксов. Например возьмем числа с интервалом в 0,1:
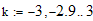
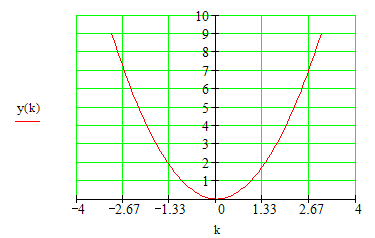
Как видим, теперь получилась более гладкая линия. Вообще графики функций по точкам строит любой комьютер в программе MathCAD или Matlab. Просто комьютер снабжен уже алгоритмом в котором выбирается заранее такой интервал между точками на оси Ох, что график всегда сразу получается плавным и непрерывным. С помощью программы маткад, мы можем построить графики основных элементарных функций и изучить их свойства.
Еще раз обращаем Ваше внимание. при построении графиков по точкам не надо никаких знаний,
Нужно только взять определенный интервал на оси Ох, как мы это сделали для параболы, взяв интервал от -3 до 3,
Выбрать на этом интервале числа и вычислить значения функции в этих числах,
Получить точки графика,
Соединяя которые плавной или ломаной линией получается сам график.
Точно также это делает MathCAD, только большой объем рутинных вычислений достается компьютеру а не человеку.
