Определение передаточной функции W(p)

Кафедра Информационно-управляющих систем

Курсовая работа по автоматике на тему: «Анализ и синтез системы автоматического управления».

Выполнил:

Вариант 18

Проверил:

Москва 2008

ОГЛАВЛЕНИЕ

Введение 4

Расчётно-графическая часть: 6

1. Определение передаточной функции W(p) 6

2.Определение передаточной функции W(p) 7

3. Определение передаточной функции W(p) 9

4. Определение передаточной функции W(p) 10

5. Расчет переходного процесса регулируемого параметра в САУ 13

6. Определение показателей качества регулирования и максимального регулируемого параметра. 15

7. Определение показателей качества регулирования 15

8. Построение ЛАЧХ 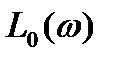не изменяемой части разомкнутой САУ 15

9. Построение желаемой ЛАЧХ 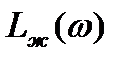17

10. Определение ЛАЧХ 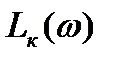корректирующего звена 19

11.Определение передаточной функции 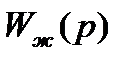разомкнутой САУ по желаемой ЛАЧХ 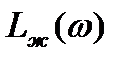19

12.Определение передаточной функции 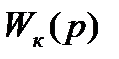корректирующего звена по ЛАЧХ 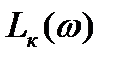20

13. Расчет переходного процесса скорректированной САУ 21

14. Определение запаса устойчивости скорректированной САУ по амплитуде и фазе. 21

15. Определение показателей качества регулирования скорректированной САУ 23

Заключение 25

Список использованных источников 26
ВВЕДЕНИЕ

Автоматическое регулирование представляет собой наиболее эффективный принцип автоматики при частичной автоматизации, когда технические средства автоматики осуществляют лишь простые функции управления, связанные с измерением, анализом, контролем различных физических величин и отработкой решений, принятых оператором в виде установок, программ или других сигналов управления.

На смену частичной пришла комплексная автоматизация, когда осуществляется автоматизация не только функций управления, но и вызванных емой выработкой этих сигналов или принятием решений, исходя из целей управления. В настоящее время системы автоматического регулирования (САР) являются основным техническим средством для создания автоматизированных производств, цехов, технологических процессов.

Сложность современных автоматических систем значительно возросла. Если в период частичной автоматизации они обычно состояли из отдельных систем автоматического регулирования, взаимная координация действий которых осуществлялась человеком, то теперь возникла необходимость в автоматической координации их действий и, следовательно, в создании сложных взаимосвязанных и многоуровневых систем автоматического регулирования (САУ). Причём, на первом уровне исследуются и автоматизируются сравнительно простые локальные процессы регулирования, а на втором и последующих – процессы управления, имеющие более общий и сложный характер.

В теории автоматического управления можно выделить две характерные задачи:

· в заданной САУ найти и оценить переходные процессы – это задача анализа САУ;

· по заданным переходным процессам и основным показателям разработать САУ – это задача синтеза САУ.

Вторая задача сложнее в виду своей неоднозначности, многое определяется творческими способностями проектировщика. Поэтому обычно задача синтеза САУ ставится ограниченно. Считается, что основная часть системы уже задана, что обычно имеет место. Требуется синтезировать корректирующие звенья, т.е. выбрать их схему и параметры. При этом необходимо, чтобы в результате коррекции САУ обеспечивался требуемый запас устойчивости, точность управления в установившихся режимах и качество управления в динамических режимах.

Синтез автоматических систем является основным и практически наиболее важным приложением результатов, полученных теорией автоматического регулирования и управления.

Синтез системы – это выбор её структуры и составных элементов – их физической природы, конструкции и параметров. При этом свойства системы должны удовлетворять некоторым заранее установленным требованиям. Предъявляются как общеинженерные требования в отношении габаритов, веса, стоимости, надёжности и т.д., так и требования специфические – к статическим и динамическим свойствам системы, к качеству регулирования.

Задачей данной курсовой работы является анализ заданной системы автоматического регулирования и последующий её синтез с целью улучшения её свойств.

РАСЧЁТНО-ГРАФИЧЕСКАЯ ЧАСТЬ

Исходные данные (вариант-18):

Дифференциальные уравнения:

1.

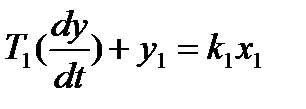
2.

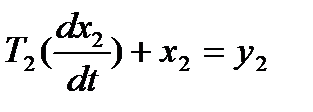
3. 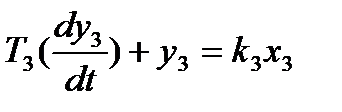(1.1)

4.

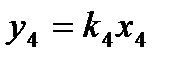
5.

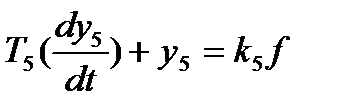
Уравнения связи элементов структурной схемы САУ:

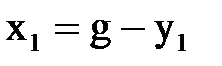
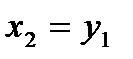
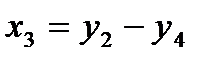(1.2)

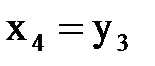
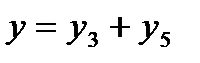
Коэффициенты дифференциальных уравнений приведены в таблице 1:

Таблица 1

k1	T1	k2	T2	k3	T3	k4	T5	k5
6,5		7,7	8,4	3,7	2,5	0,27	2,2	1,7

Решение:

Определение передаточной функции W(p)

По заданным дифференциальным уравнениям элементов системы автоматического управления определим передаточные функции W(p). Для этого заменим в дифференциальных уравнениях 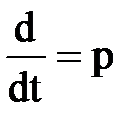и подставим значения коэффициентов в уравнения (1.1):

1.

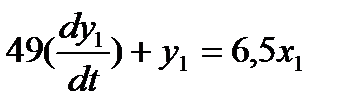
2.

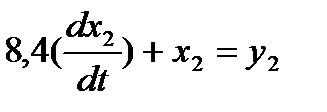
3.

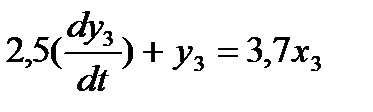
4.

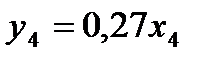
5.

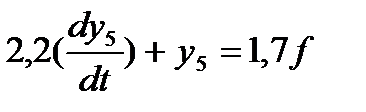
1. 49pY1(p)+Y1(p)=6,5X1(p)

2. 8,4X2(p)+X2(p)=Y2(p)

3. 2,5pY3(p)+Y3(p)=3,7X3(p)

4. 0,27X4(p)=Y4(p)

5. 2,2pY5(p)+Y5(p)=1,7F(p)

1. (49P+1)Y1(P)=6,5X1(P)

2. (8,4P+1)X2(P)=Y2(P)

3. (2,5P+1)Y3(P)=3,7X3(P)

4. 0,27X4(P)=Y4(P)

5. (2,2P+1)Y5(P)=1,7F(P)

так как y(p)=W(p)∙x(p), то передаточные функции W(p)равны:

1.

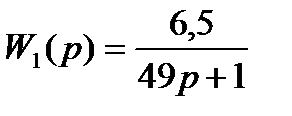
2.

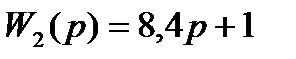
3.

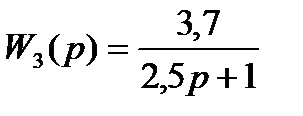
4.

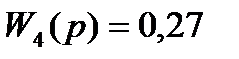
5.

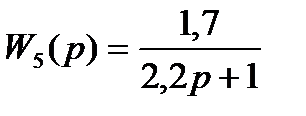
2. Построение структурной схемы САУ и определение передаточных функций замкнутой САУ по каналам управляющего и возмущающего воздействий.

По заданным уравнениям (1.2) связи элементов построим структурную схему САУ:

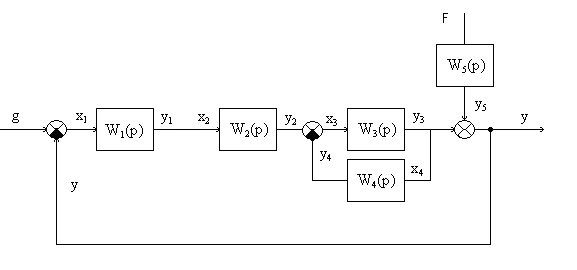
Рис.1 Структурная схема САУ, построенная на основе уравнений связи

Определение передаточной функции замкнутой САУ.

Упростим схему объединив W3(p) и W4(p)

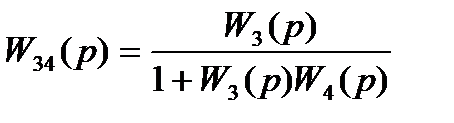(1.3)

Определим передаточную функцию разомкнутой системы W(p)раз.сис

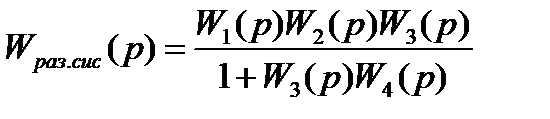(1.4)

Определим передаточную функцию замкнутой системы W(p)зам.сис

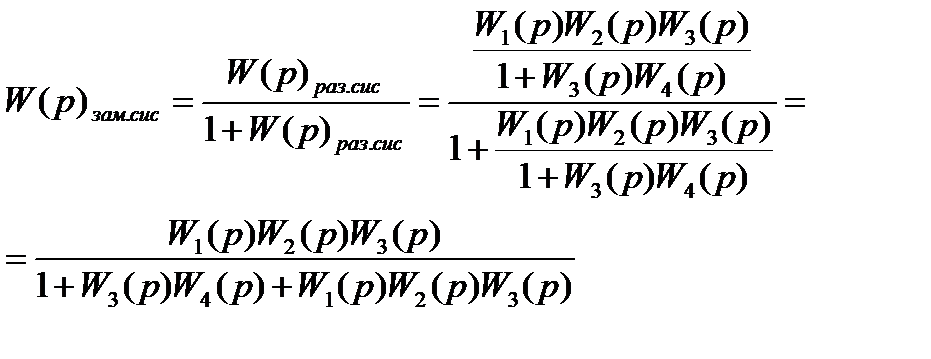(1.5)

Определим передаточную функцию замкнутой системы по каналу возмущающего воздействия W(p)f

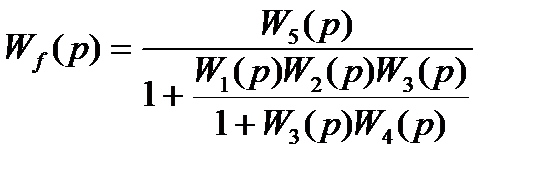(1.6)

Подставим уравнения элементов структуры в уравнение (1.5):

Полученную функцию исследуем на устойчивость замкнутой САУ по критериям устойчивости Гурвица и Михайлова.

3. Исследование на устойчивость замкнутой САУ по критериям устойчивости Гурвица и Михайлова.

Определение устойчивости САУ по критерию Гурвица

Возьмем характеристическое уравнение:

D(p)=122,5p² +302,471p +26,049

Если характеристическое уравнение имеет первый или второй порядок, то для устойчивости достаточно, что бы коэффициенты a0, a1, a2, были больше нуля.

Как видно из нашего характеристического уравнения коэффициенты a0>0 a1>0 a2>0, что является условие устойчивости САУ по критерию Гурвица.

Определение устойчивости САУ по критерию Михайлова

Возьмем наше характеристическое уравнение:

D(p)=122,5p² +302,471p +26,049

Подставив в уравнение p=jω и получим:

D(jω)=122,5 (jω)²+301,471 jω+26,049= -122,5ω²+301,471 jω+26,049

Выделим в данном уравнении вещественную и мнимую части:

Re(w)=26,049-122,5w²

Im(w)=302,471w

Зависимость от частоты реальной и мнимой частей характеристического уравнения представлена в таблице 2 и на рис. 2.

Таблица 2

w		0,2	0,5		1,2	1,5
Re	26,049	21,149	-4,576	-96,451	-150,35	-249,58	-463,95
Im		60,5	151,24	302,47	362,97	453,7	604,94

Из рис. 2 видно, что годограф обходит начало координат в следующем порядке: 1ый квадрант, 2ой квадрант. Это является условием устойчивости САУ по критерию Михайлова.

4. Определение области устойчивости САУ методом D-разбиения

Определим область устойчивости САУ методом D-разбиения по коэффициенту усиления K4. Возьмем передаточную функцию замкнутой системы W(p)раз.сис уравнение (1.5)

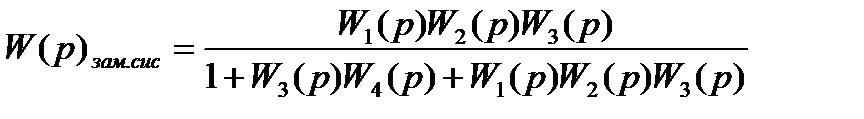
Подставим значения передаточных функций в передаточную функцию замкнутой системы W(p)раз.сис, получим:

Из полученного выражения возьмем характеристическое уравнение замкнутой системы автоматического управления:

D(p)=122,5p² +253,52p +25,01+K4(3,7+181,3p)

Запишем характеристическое уравнение в виде:

S(p)= 122,5p² +253,52p +25,01

N(p)= 3,7+181,3p

S(p)+K4 N(p)=0 от сюда K4=-S(p)/N(p)

Заменим p=jω и S(jω) и N(jω), получим:

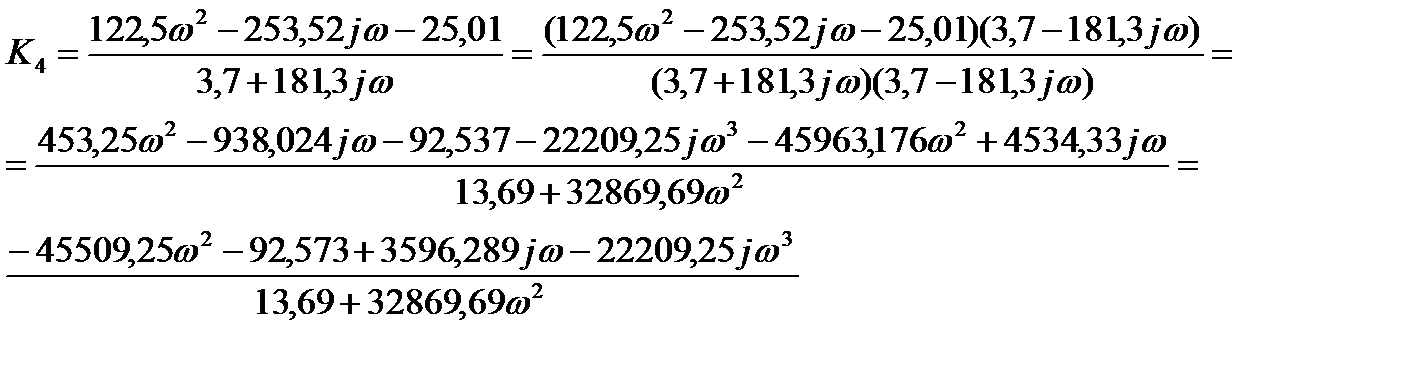
Выделим в данном уравнении вещественную и мнимую части:

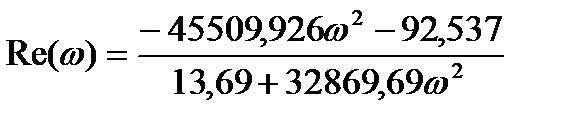
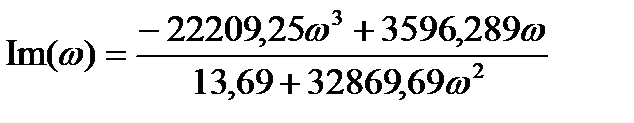
Зависимость от частоты реальной и мнимой частей характеристического уравнения представлена в таблице 3 и на рис. 3.

Таблица 3

ω	0,00	0,03	0,06	0,09	0,12	0,15	0,18	0,21	0,27	0,33	0,36	0,80
Re	-6,76	-3,08	-1,94	-1,65	-1,54	-1,48	-1,45	-1,43	-1,42	-1,41	-1,40	-1,39
Im	0,00	2,48	1,60	1,10	0,81	0,62	0,48	0,38	0,22	0,11	0,06	-0,40

Осуществим проверку с помощью критерия Гурьвица, для этого в характеристическое уравнение подставим значения К4 из области устой-чивости и не устойчивости.

Подставим значение из области устойчивости K4=-1, получим:

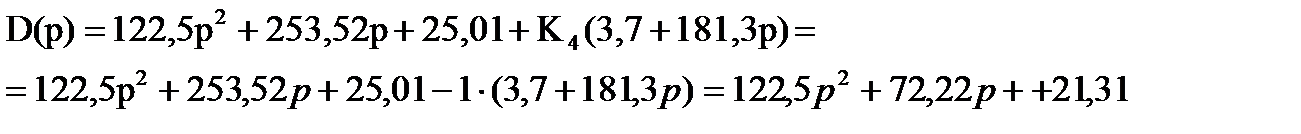
Видно что коэффициенты 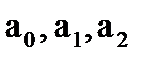, больше нуля, значит система устойчива.

Подставим значение из области не устойчивости K4=-2, получим:

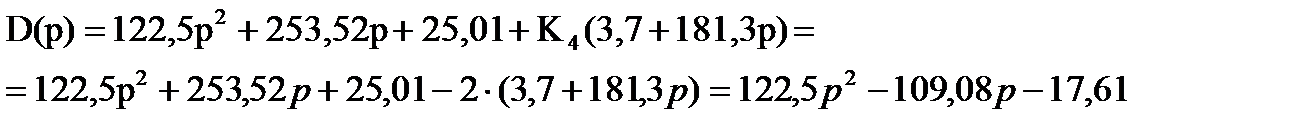
Видно что коэффициент 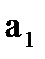меньше нуля, значит система не устойчива.

Проверка показала, область устойчивости была верно определена методом D-разбиения.

5. Расчет переходного процесса регулируемого параметра в САУ.

На рис. 4 представлена структурная схема САУ в программе МВТУ для расчета переходного прочеса по каналу управляющего воздействия.

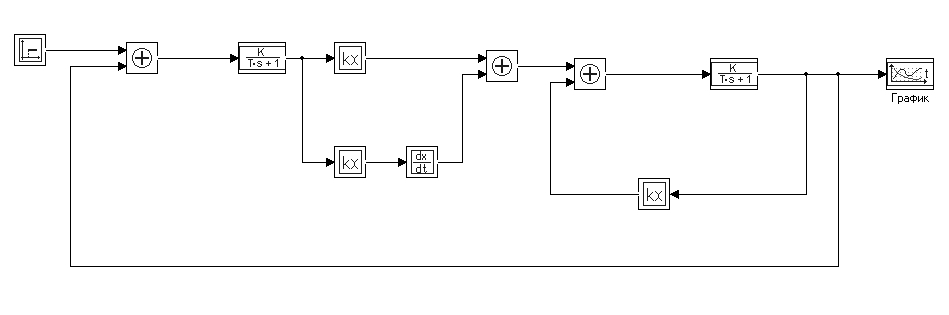
рис. 4 структурная схема САУ в программе МВТУ для расчета переходного прочеса по каналу управляющего воздействия.

На рис. 5 представлена кривая в программе МВТУ переходного процесса.

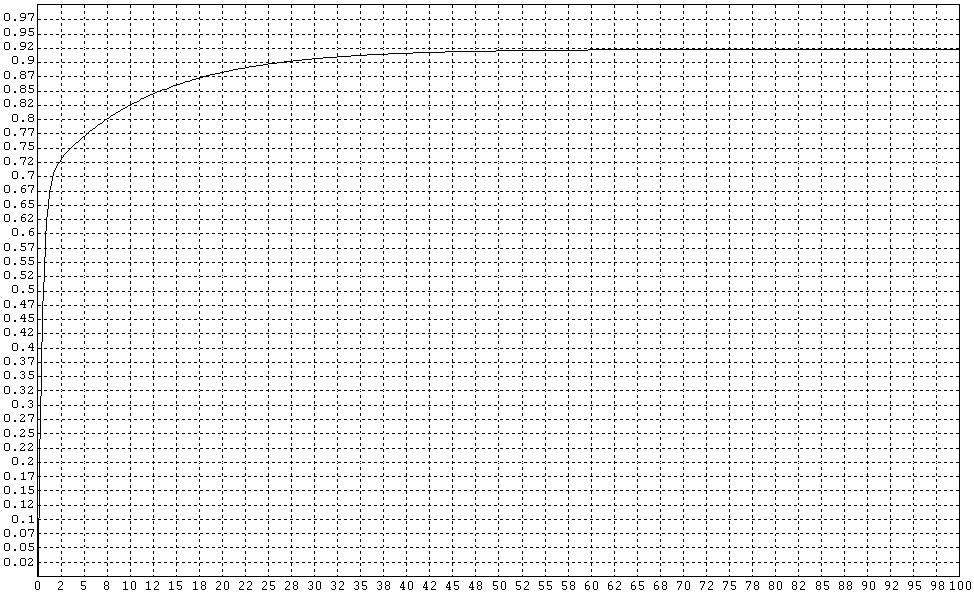
рис. 5 кривая в программе МВТУ переходного процесса.

6. Определение показателей качества регулирования и максимального регулируемого параметра.

По кривой представленной на рис. 5 определим время регулирования.

Для этого на кривой отмечаем 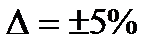от 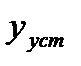, и проводим линии параллельные оси абцис. На пересечении кривой и нижней линии получаем точку это и есть время регулирования 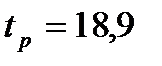. На рис. 6 представлена часть кривой переходного процесса.

По кривой представленной на рис.6 определяем максимальное ускорение .

Для этого проводим касательные к точкам 0 и 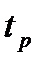и строим треугольники. Скорости находятся как отношений приращений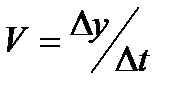

Получив скорости 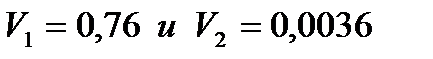подставляем в формулу для максимального ускорения :

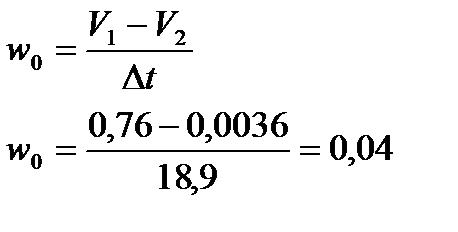
7. Определение показателей качества регулирования.

Показатели качества регулирования вычисляются по следующим формулам: 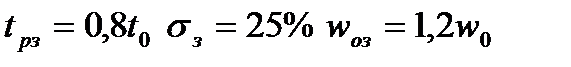. Получим:

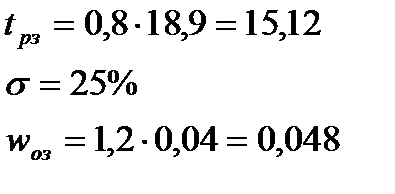
8. Построение ЛАЧХ 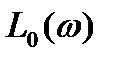не изменяемой части разомкнутой САУ.

Возьмем передаточную функцию разомкнутой САУ формула (1.4)

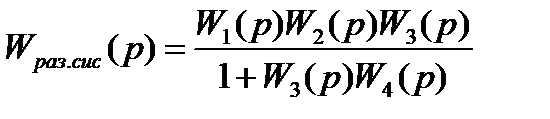
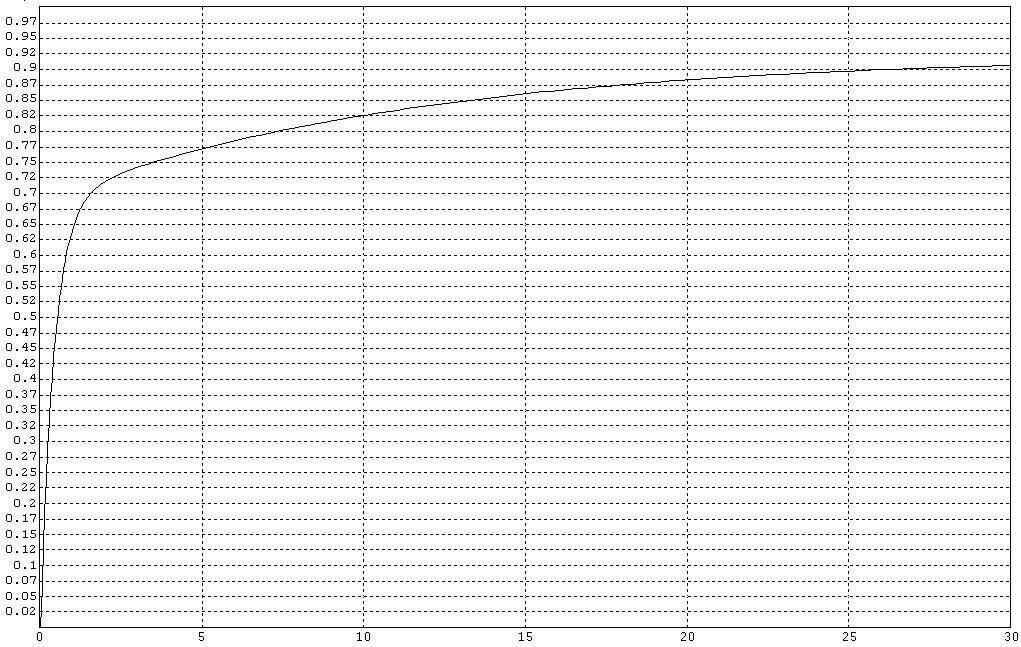
рис. 6 часть кривой переходного процесса

Подставив значения передаточных функций получим:

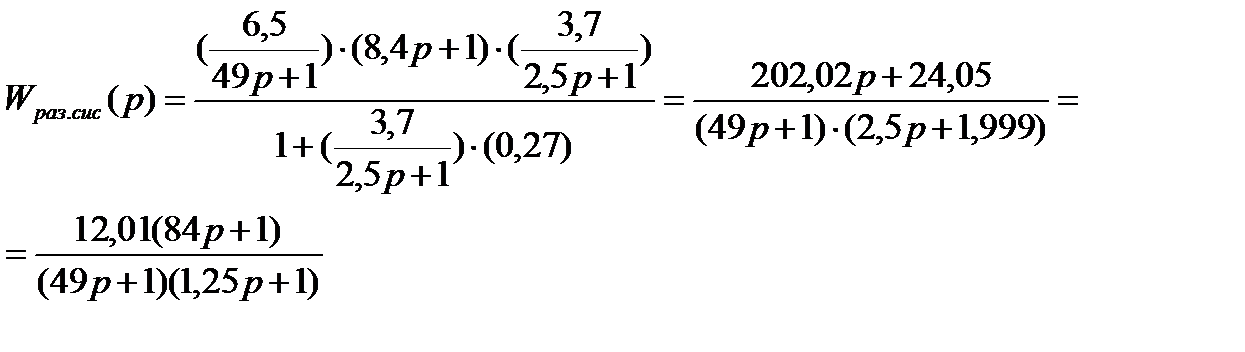
Найдем сопряженные частоты:

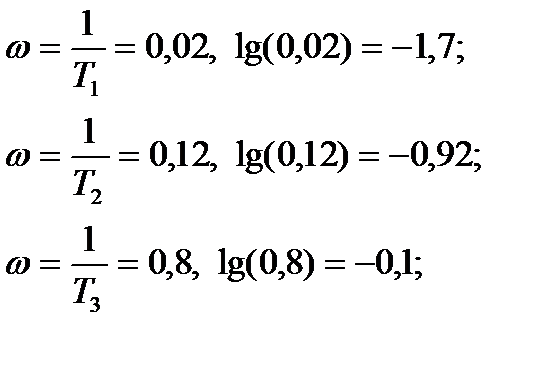
На рис.7 представлена ЛАЧХ 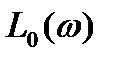не изменяемой части разомкнутой САУ.

9. Построение желаемой ЛАЧХ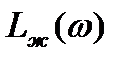

Для построения желаемой ЛАЧХ 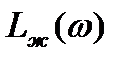, найдем частоту среза 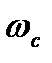, для среднечастотной асимптоты. Для этого используем номограмму, составленная В.В. Солодниковым на рис. 8. По заданному значению перерегулирования определим отношение между 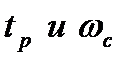. Используя формулу :

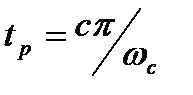. (1.7)

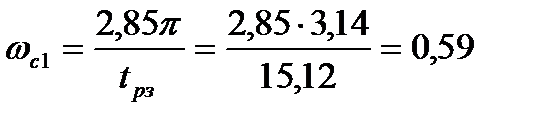Дано , от сюда получаем , тем самым мы нашли частоту при которой время регулирования не превысит заданного значения. При начальном рассогласовании ускорение регулируемой величины ограничивается значением 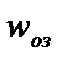, то максимальное значение определяется из отношения:

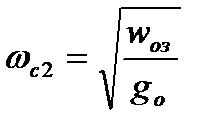, (1.8) где 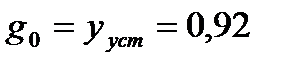. Получим:

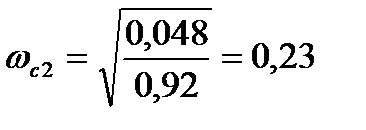
Т.к. 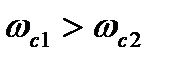, то частоту среза принимаем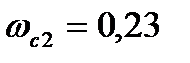

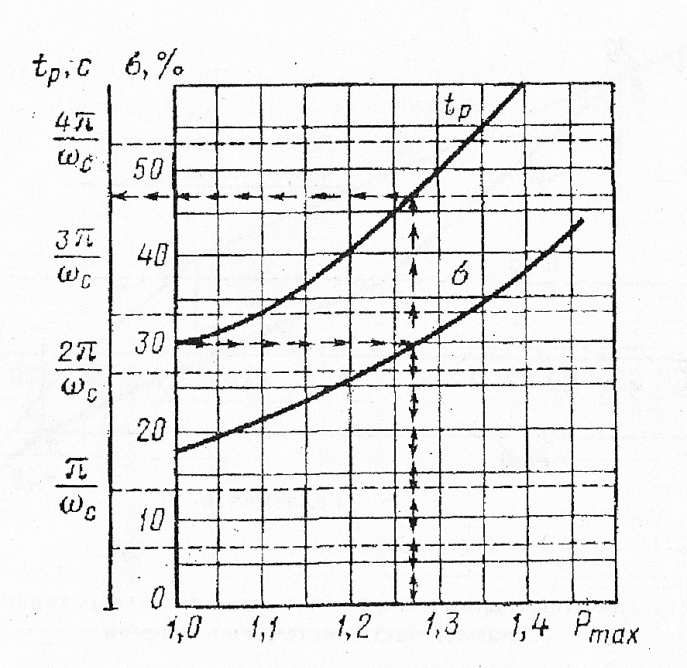
Рис.8 Показатели качества регулирования САУ в зависимости от максимума вещественной частотной характеристики разомкнутой системы.

Средне частотная асимптота желаемой ЛАЧХ проводится через частоту среза с наклоном -20 дБ/дек.

Найдем частоту сопряжения с низкочастотной областью. Для этого воспользуемся номограммой на рис. 9, по ней определяем предельные значения логарифмических амплитуд. В нашем случае это значение 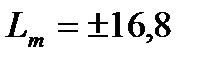. На этих отметках проводим линии параллельные оси частот. В точках пересечения этих линий и средне частотной асимптоты мы получаем сопрягающие частоты. Для определения низкочастотной области воспользуемся следующим выражением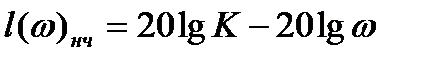

Возьмем ω=1 получим: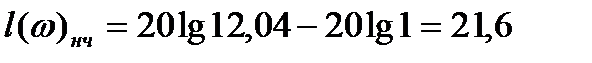

Возьмем ω=К получим: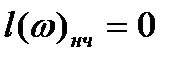

По этим 2 тучкам строем наклонную линию АВ, её наклон -20дБ/дек.

Из точки сопряжения низкочастотной и средне частотной проводим наклонную, с наклоном -40дБ/дек, до пересечения с линией АВ.

Высоко частотную асимптоту проводим параллельно желаемой ЛАЧХ, т.к. она мало влияет на свойства системы.

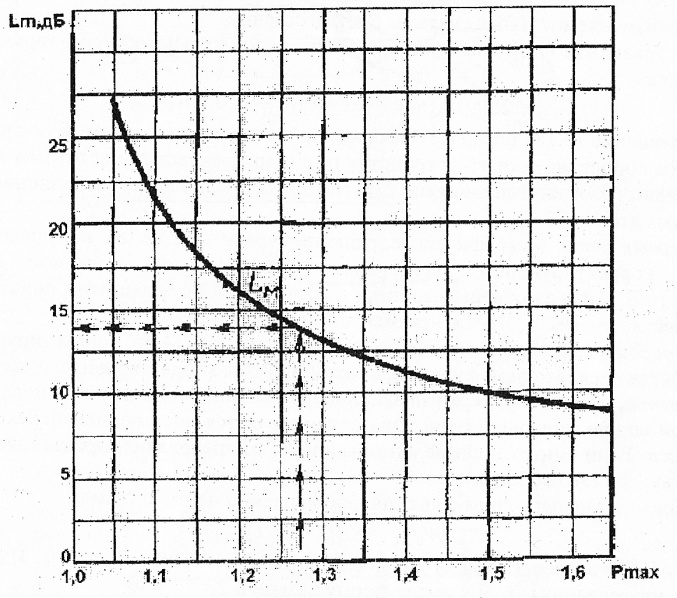
Рис. 9 Зависимость значений желаемой ЛАЧХ на границах среднего поддиапазона от максимума вещественной частотной характеристики разомкнутой системы.

На рис.7 представлена желаемая ЛАЧХ .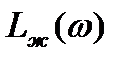

10. Определение ЛАЧХ 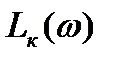корректирующего звена.

Т.к в нашей системе корректирующее звено последовательное, то для построения ЛАЧХ 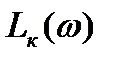корректирующего звена, воспользуемся формулой:

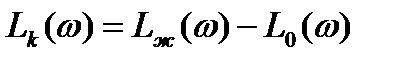(1.9).

На рис.7 представлена ЛАЧХ 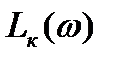корректирующего звена.

11. Определение передаточной функции 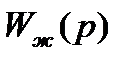разомкнутой САУ по желаемой ЛАЧХ .

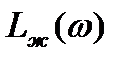Для определения передаточной функции 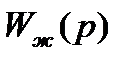разомкнутой САУ по желаемой ЛАЧХ 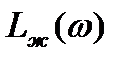воспользуемся рис.7. Получим:

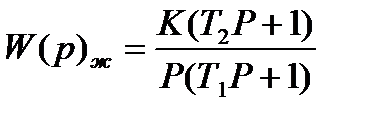(1.10)

Найдем частоты сопряжения и получим Т

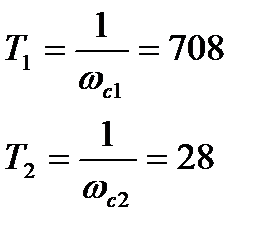
По ЛАЧХ 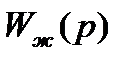показанной на рис.7 найдем К=21,6

Подставим найденные Т, получим

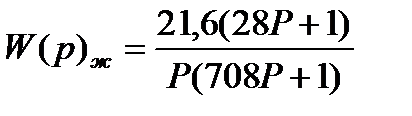
12. Определение передаточной функции 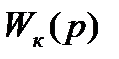корректирующего звена по ЛАЧХ .

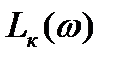Для определения передаточной функции 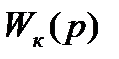разомкнутой САУ корректирующего звена по полученной ЛАЧХ 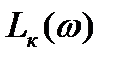воспользуемся рис.7. Получим:

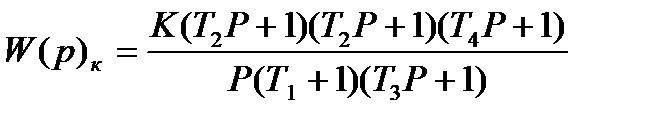(1.11)

Найдем частоты сопряжения и получим Т

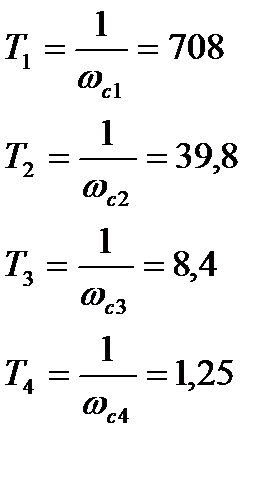
По ЛАЧХ показанной на рис.7 найдем К=1.

Подставим найденные Т и К в выражение (1.11), получим

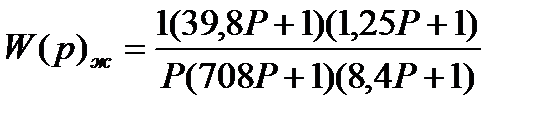
13. Расчет переходного процесса скорректированной САУ.

На рис. 9 представлена структурная схема скорректированной САУ в программе МВТУ для расчета переходного прочеса по каналу управляющего воздействия.

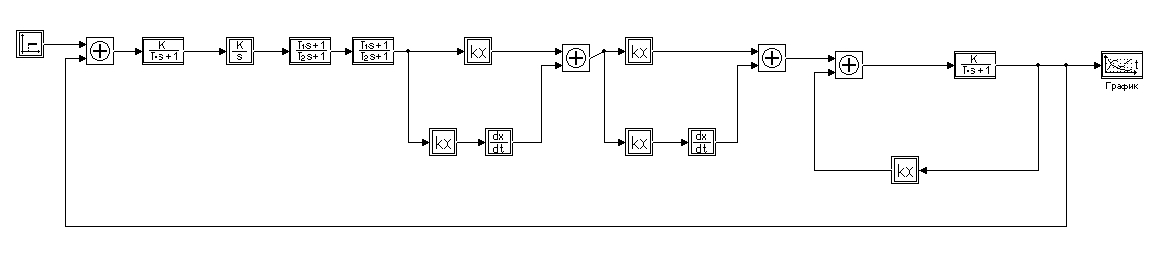
рис. 9 структурная схема скорректированной САУ в программе МВТУ для расчета переходного прочеса по каналу управляющего воздействия.

На рис. 10 представлена кривая в программе МВТУ переходного процесса.

14. Определение запаса устойчивости скорректированной САУ по амплитуде и фазе.

Для определения запаса устойчивости по фазе из точки пересечения ЛАЧХ с осью частот опускается вертикаль до угла -180, при этом отрезок между кривой ЛФЧХ и уровнем -180 даст величину запаса устойчивости.

Для определения запаса устойчивости по амплитуде, необходимо восстановить вертикаль из точки пересечения ЛФЧХ с линией -180 до пересечения с осью частот. При этом отрезок между графиком ЛАЧХ и осью абсцисс даст нам величину запаса по амплитуде.

Из выражения 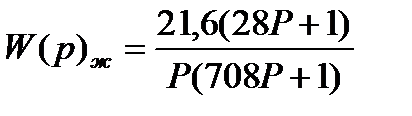, запишем ФЧХ:

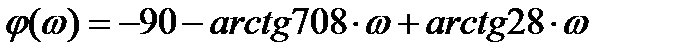
Значения ФЧХ при разных ω представлены в таблице 4.

Таблица 4

ω		0,001	0,005	0,01	0,05	0,1	0,5
φ(ω)	-90	-123,7	-156	-156,3	-124	-109	-94	-91,6

На рис.11 показано нахождение запаса устойчивости по фазе и амплитуде.

.

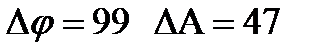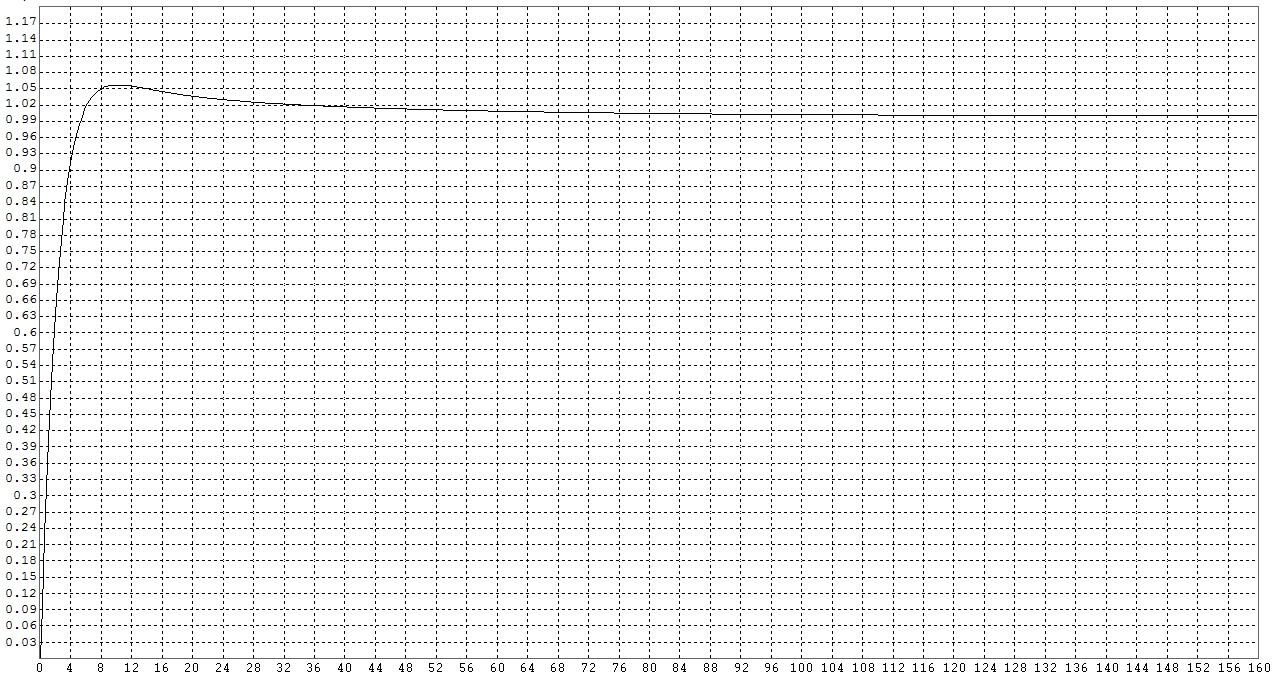
рис. 10 кривая в программе МВТУ переходного процесса.