Глава 4. системы одновременных уравнений
4.1. Структурная форма уравнений
Структурная форма модели(системы одновременных уравнений) – это система уравнений, в каждом из которых помимо объясняющих (независимых) переменных могут содержаться объясняемые (зависимые) переменные из других уравнений. Уравнения, составляющие исходную модель, называются структурными уравнениями модели.
Простейшая структурная форма модели имеет вид:
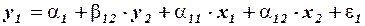 ,
,
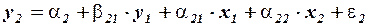 ,
,
где:
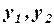 и
и 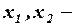 зависимые и независимые переменные;
зависимые и независимые переменные;
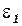 и
и 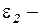 случайные слагаемые;
случайные слагаемые;
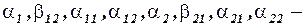 параметры модели.
параметры модели.
Параметры структурной формы модели называются структурными коэффициентами.
Структурная форма модели включает в систему не только уравнение, отражающее взаимосвязи между отдельными переменными, но и уравнения, отражающие тенденцию развития явления – функции времени, а также разного рода уравнения-тождества. Тождества не содержат каких-либо подлежащих оценке параметров, а также не включают случайных слагаемых.
В процессе оценивания параметров одновременных уравнений следует различать эндогенные (внутренние, зависимые) и экзогенные переменные. Эндогеннымисчитаются переменные, значения которых определяются внутри модели. Это зависимые переменные, число которых равно числу уравнений системы. Экзогенными(внешними, независимыми) считаются переменные, значения которых определяются вне модели. Это заданные переменные, влияющие на эндогенные переменные, но не зависящие от них.
В качестве экзогенных могут рассматриваться значения эндогенных переменных за предшествующий период времени.
Обычно в каждом уравнении предполагается отсутствие корреляции экзогенных переменных со случайной составляющей. Однако в общем случае может иметь место корреляция эндогенных переменных со случайной составляющей, из-за которой использование метода МНК приводит к несостоятельным оценкам структурных коэффициентов. Поэтому для определения этих коэффициентов структурные уравнения модели преобразуют в приведенную форму.
4.2. Приведенная форма уравнений
Приведенной формой уравнений называется система уравнений, в каждом из которых эндогенные переменные выражены только через экзогенные переменные и случайные составляющие. Уравнения, составляющие исходную модель, называют структурными уравнениями модели.
Приведенная форма простейшей исходной модели имеет вид:
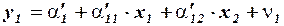 ,
,
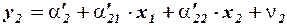 ,
,
где:
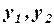 и
и 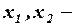 зависимые и независимые переменные;
зависимые и независимые переменные;
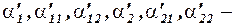 параметры приведенной формы модели;
параметры приведенной формы модели;
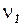 и
и 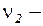 случайные слагаемые.
случайные слагаемые.
Параметры – коэффициенты приведенной формы модели системы уравнений называются коэффициенты приведенной формы (приведенными коэффициентами). Они оцениваются обычным методом наименьших квадратов (МНК), поскольку экзогенные переменные не коррелированны со случайными слагаемыми.
Рассчитанные коэффициенты приведенной формы могут быть использованы для оценивания структурных коэффициентов. Такой способ оценивания структурных коэффициентов называется косвенным методом наименьших квадратов (КМНК).
Структурные коэффициенты можно однозначно выражать через приведенные коэффициенты, или они могут иметь несколько разных оценок, но совсем не выражаться через них.
Структурный коэффициент называется идентифицируемым, если его можно точно вычислить на основе приведенных коэффициентов, точно идентифицируемым, если он имеет единственную оценку, и сверхидентифицируемым, если он имеет несколько разных оценок. В противном случае он называется неидентифицируемым.
Структурное уравнение являетсяидентифицируемым, если идентифицируемы все его коэффициенты. Если хотя бы один структурный коэффициент неидентифицируем, то и все уравнение является неидентифицируемым.
Модель считается идентифицируемой, если каждое ее уравнение идентифицируемо. Если хотя бы одно из уравнений системы неидентифицируемо, то и вся модель является неидентифицируемой.
В зависимости от вида системы одновременных уравнений коэффициенты структурной модели могут быть оценены различными способами. Наиболее распространены следующие методы:
· метод инструментальных переменных (ИП);
· косвенный метод наименьших квадратов (КМНК);
· двухшаговый метод наименьших квадратов (ДМНК).
4.3. Случай идентифицируемости: косвенный метод наименьших квадратов и метод инструментальных переменных
Предположим, что необходимо оценить параметры уравнения функции потребления в простой модели Кейнса формирования доходов:
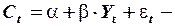 функция потребления,
функция потребления,
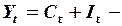 тождество доходов,
тождество доходов,
где:
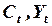 и
и 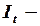 объем потребления, совокупный доход и инвестиции соответственно;
объем потребления, совокупный доход и инвестиции соответственно;
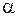 и
и 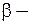 структурные коэффициенты, причем
структурные коэффициенты, причем 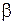 характеризует предельную склонность к потреблению;
характеризует предельную склонность к потреблению;
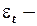 случайное слагаемое.
случайное слагаемое.
В исходной модели 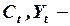 эндогенные (внутренние, зависимые) переменные,
эндогенные (внутренние, зависимые) переменные, 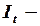 экзогенная – внешняя, независимая переменная. Непосредственное оценивание параметров
экзогенная – внешняя, независимая переменная. Непосредственное оценивание параметров 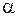 и
и 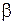 в структурном уравнении функции потребления дает смещенные и несостоятельные оценки, так как объясняющая переменная
в структурном уравнении функции потребления дает смещенные и несостоятельные оценки, так как объясняющая переменная 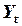 является эндогенной зависимой переменной. Разрешая структурную систему относительно эндогенных переменных, можно получить приведенную систему уравнений:
является эндогенной зависимой переменной. Разрешая структурную систему относительно эндогенных переменных, можно получить приведенную систему уравнений:

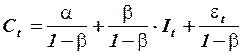 ,
,
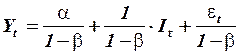 .
.
В приведенной системе уравнений коэффициенты при переменной 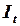 , равные
, равные 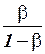 и
и 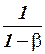 , представляют собой инвестиционные мультипликаторы потребления и дохода соответственно. Они показывают: если объем инвестиций возрастает на 1, то объем потребления увеличится на
, представляют собой инвестиционные мультипликаторы потребления и дохода соответственно. Они показывают: если объем инвестиций возрастает на 1, то объем потребления увеличится на 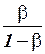 , а совокупный доход возрастет на
, а совокупный доход возрастет на 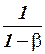 .
.
Известны разные методы оценивания структурных коэффициентов 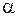 и
и 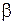 .
.
Косвенный метод наименьших квадратов (КМНК). Уравнение для 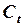 в приведенной форме имеет вид:
в приведенной форме имеет вид:
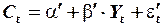 ,
,
где 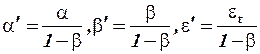 .
.
Уравнение в приведенной форме включает экзогенную переменную 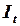 , которая некоррелирована со случайным слагаемым
, которая некоррелирована со случайным слагаемым 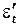 , поэтому для оценки параметров
, поэтому для оценки параметров 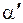 и
и 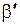 можно использовать обычный метод наименьших квадратов.
можно использовать обычный метод наименьших квадратов.
Оцененное с помощью МНК уравнение в приведенной форме, полученное по выборочным данным, будет иметь вид:
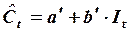 ,
,
где 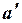 и
и 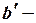 оценки параметров
оценки параметров 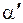 и
и 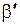 .
.
Полученные таким образом оценки будут представлять собой несмещенные и состоятельные оценки параметров 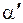 и
и 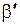 .
.
Используя приведенные выше соотношения параметров исходной (структурной) системы уравнений и приведенной системы уравнений, можно получить оценки параметров структурной системы уравнений:
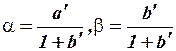 .
.
Поскольку получены единственные оценки 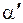 и
и 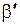 структурных коэффициентов через оценки
структурных коэффициентов через оценки 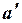 и
и 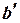 приведенных коэффициентов, то структурное уравнение функции потребления является однозначно определенным – точно идентифицируемым.
приведенных коэффициентов, то структурное уравнение функции потребления является однозначно определенным – точно идентифицируемым.
Проблема коррелированности объясняющей переменной 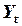 со случайным слагаемым
со случайным слагаемым 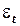 в структурном уравнении для
в структурном уравнении для 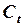 может быть разрешена с помощью метода инструментальных переменных. Для применения этого метода необходимо найти такую инструментальную переменную, которая обладает следующими свойствами:
может быть разрешена с помощью метода инструментальных переменных. Для применения этого метода необходимо найти такую инструментальную переменную, которая обладает следующими свойствами:
1) коррелируется с неудачно объясняющей переменной 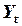 ;
;
2) не коррелируется со случайным слагаемым 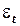 .
.
В рассматриваемом примере в качестве инструментальной переменной может быть использована величина 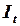 . Она коррелированна с
. Она коррелированна с 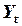 , так как
, так как 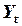 зависит от
зависит от 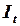 (что следует из исходных уравнений), и не коррелируется с
(что следует из исходных уравнений), и не коррелируется с 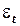 , поскольку является экзогенной (внешней) переменной.
, поскольку является экзогенной (внешней) переменной.
4.4. Случай сверхидентифицируемости: метод инструментальных переменных и двухшаговый метод наименьших квадратов (ДМНК)
Случай сверхидентифицируемой системы уравненийрассмотрим на примере модели формирования доходов Кейнса:
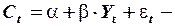 функция потребления,
функция потребления,
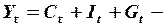 тождество доходов,
тождество доходов,
где:
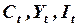 и
и 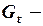 объем потребления, совокупный доход, инвестиции и государственные расходы соответственно;
объем потребления, совокупный доход, инвестиции и государственные расходы соответственно;
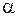 и
и 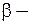 структурные коэффициенты, причем
структурные коэффициенты, причем 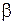 характеризует предельную склонность к потреблению;
характеризует предельную склонность к потреблению;
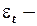 случайное слагаемое.
случайное слагаемое.
В исходной модели 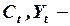 эндогенные переменные,
эндогенные переменные, 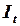 и
и 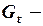 экзогенные.
экзогенные.
Разрешая структурную систему относительно эндогенных переменных, получим приведенную систему уравнений вида:
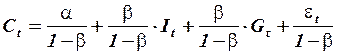 ,
,
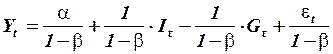 .
.
Для оценивания структурных коэффициентов 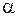 и
и 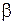 используются различные методы.
используются различные методы.
Метод инструментальных переменных. В структурном уравнениифункции потребления в качестве инструментальных переменных для 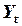 можно использовать
можно использовать 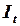 или
или 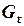 . В зависимости от выбора инструментальной переменной полученные оценки
. В зависимости от выбора инструментальной переменной полученные оценки 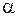 и
и 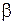 будут различаться, но в обоих случаях они будут состоятельными. Поэтому в данном случае в качестве инструментальной переменной наиболее целесообразно выбрать комбинацию
будут различаться, но в обоих случаях они будут состоятельными. Поэтому в данном случае в качестве инструментальной переменной наиболее целесообразно выбрать комбинацию 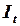 и
и 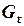 .
.
Структурное уравнение с избыточным числом экзогенных переменных, которые можно использовать как инструментальные, является переопределенным (сверхидентифицируемым).
Двухшаговый метод наименьших квадратов(ДМНК). Двухшаговый МНК можно рассматривать как частный случай конструирования наилучшей из возможных комбинаций инструментальных переменных, если в качестве последних использовать избыточные экзогенные переменные, имеющиеся в уравнении. Выше было отмечено, что при использовании метода инструментальных переменных структурное уравнениефункции потребления оказывается переопределенным, и потому для определения функции 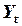 выбирается линейная комбинация двух переменных
выбирается линейная комбинация двух переменных 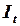 и
и 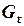 :
:
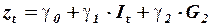 ,
,
где 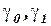 и
и 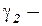 коэффициенты, подлежащие оценке.
коэффициенты, подлежащие оценке.
На первомшаге ДМНК вместо переменной 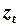 может быть выбрана регрессионная оценка
может быть выбрана регрессионная оценка 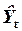 приведенного уравнения для переменной
приведенного уравнения для переменной 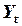 с помощью обычного МНК:
с помощью обычного МНК:
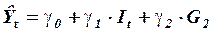 .
.
Подставляя теоретические значения 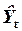 в структурное уравнениефункции потребления (вместо фактических значений), получают уравнение:
в структурное уравнениефункции потребления (вместо фактических значений), получают уравнение:
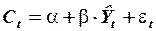 .
.
На второмшаге ДМНК обычным методом МНК оценивают параметры 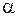 и
и 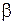 этого уравнения. При этом оценки структурных коэффициентов будут состоятельными.
этого уравнения. При этом оценки структурных коэффициентов будут состоятельными.
Двухшаговый МНК можно рассматривать как способ конструирования наилучшей из возможных комбинаций инструментальных переменных, если в уравнении имеется избыток экзогенных переменных, которые можно использовать как инструментальные.
4.5. Случай неидентифицируемости
В случае неидентифицируемостиструктурной модели в нее необходимо ввести новые переменные, с помощью которых можно было бы добиться идентифицируемости модели. Рассмотрим модель спроса и предложения:
уравнение спроса: 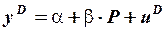 ,
,
уравнение предложения: 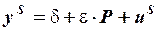 ,
,
тождество равновесия: 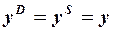 ,
,
где:
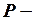 цена товара;
цена товара;
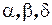 и
и 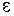 – параметры;
– параметры;
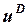 и
и 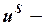 случайные слагаемые.
случайные слагаемые.
Переменные 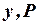 являются эндогенными, их значения определяются в процессе установления рыночного равновесия.
являются эндогенными, их значения определяются в процессе установления рыночного равновесия.
В рассматриваемой модели нет экзогенных переменных, поэтому ни одно из этих уравнений не является идентифицируемым. Чтобы модель имела статистическое решение, в нее необходимо ввести экзогенные переменные.
Если все продавцы товара облагаются специальным налогом 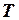 , который они должны платить с выручки, то данные об этом налоге могут быть включены в состав данных, используемых для анализа. При этом уравнения спроса останется неизменным, если переменная
, который они должны платить с выручки, то данные об этом налоге могут быть включены в состав данных, используемых для анализа. При этом уравнения спроса останется неизменным, если переменная 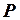 означает рыночную цену, а уравнение предложения изменится. Система примет вид:
означает рыночную цену, а уравнение предложения изменится. Система примет вид:
уравнение спроса: 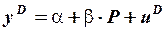 ,
,
уравнение предложения: 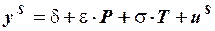 ,
,
тождество равновесия: 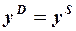 ,
,
где:
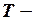 экзогенная переменная;
экзогенная переменная;
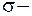 дополнительный параметр.
дополнительный параметр.
Уравнение спроса будет идентифицируемым, поскольку переменная 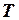 не включена в него и может выступать в качестве инструментальной для переменной
не включена в него и может выступать в качестве инструментальной для переменной 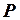 , а уравнение предложения – неидентифицируемым.
, а уравнение предложения – неидентифицируемым.
В уравнение спроса можно включить переменную 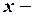 доход на душу населения, при этом система примет вид:
доход на душу населения, при этом система примет вид:
уравнение спроса: 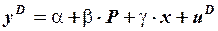 ,
,
уравнение предложения: 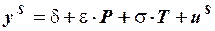 ,
,
тождество равновесия: 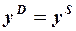 ,
,
где:
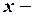 экзогенная переменная – доход на душу населения;
экзогенная переменная – доход на душу населения;
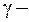 дополнительный параметр.
дополнительный параметр.
Экзогенную переменную 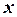 можно использовать в качестве инструментальной переменной для уравнения спроса. В итоге полученная модель представляет собой точно идентифицируемуюмодель спроса и предложения.
можно использовать в качестве инструментальной переменной для уравнения спроса. В итоге полученная модель представляет собой точно идентифицируемуюмодель спроса и предложения.
4.6. Применение ограничений коэффициентов системы уравнений
В некоторых случаях неидентифицируемаямодель может быть превращена в идентифицируемуюпутем задания соотношения между структурными коэффициентами. Такой метод носит название метода ненулевого ограничения. Рассмотрим этот метод на примере неидентифицируемоймодели спроса и предложения:
уравнение спроса: 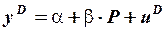 ,
,
уравнение предложения: 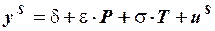 ,
,
тождество равновесия: 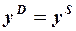 ,
,
где:
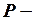 цена товара;
цена товара;
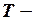 экзогенная переменная – налог с продаж;
экзогенная переменная – налог с продаж;
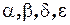 и
и 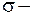 параметры;
параметры;
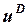 и
и 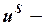 случайные слагаемые.
случайные слагаемые.
Улучшить спецификацию модели можно, введя ограничение на коэффициенты 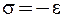 . Тогда система исходных данных – структурных уравнений преобразуется к виду:
. Тогда система исходных данных – структурных уравнений преобразуется к виду:
уравнение спроса: 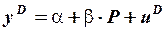 ,
,
уравнение предложения: 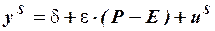 ,
,
тождество равновесия: 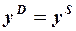 .
.
Благодаря введению ограничения на коэффициенты уравнение предложения стало идентифицируемым. Действительно, преобразованную систему можно рассмотреть как новую версию модели – систему из 4 уравнений:
уравнение спроса: 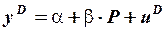 ,
,
уравнение предложения: 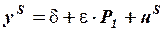 ,
,
тождество цены товара для продавца 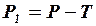 ,
,
тождество равновесия: 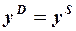 ,
,
где: 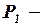 цены товара для продавца (сумма, остающаяся у продавца после уплаты налога).
цены товара для продавца (сумма, остающаяся у продавца после уплаты налога).
Последние два уравнения системы являются уравнениями-тождествами и не требуют проверки на идентификацию. Переменная 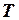 не включена в уравнение спроса, поэтому она может быть использована в качестве инструментальной для переменной
не включена в уравнение спроса, поэтому она может быть использована в качестве инструментальной для переменной 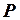 . В результате с помощью метода наименьших квадратов можно получить уравнение регрессии вида:
. В результате с помощью метода наименьших квадратов можно получить уравнение регрессии вида:
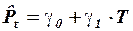 ,
,
где 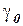 и
и 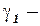 коэффициенты, подлежащие оценке.
коэффициенты, подлежащие оценке.
Так как переменная 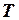 не включена в уравнение предложения, то она также может использоваться в качестве инструментальной для переменной
не включена в уравнение предложения, то она также может использоваться в качестве инструментальной для переменной 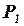 . Полученная модель в целом является точно определенной(точно идентифицируемой).
. Полученная модель в целом является точно определенной(точно идентифицируемой).
Таким образом, наличие ограничения на коэффициенты системы уравнений (называемого ненулевым ограничением) позволяет исключить одну объясняющую переменную из уравнения. Если эта переменная эндогенная, для нее не нужно искать инструментальную переменную; если экзогенная, то она может использоваться в качестве инструментальной для одной из эндогенных переменных, оставшихся в уравнении.
4.7. Порядковое условие для идентификации уравнений
Коэффициенты системы уравнений приведенной формы оцениваются обычным методом наименьших квадратов (МНК), если экзогенные переменные не коррелированны со случайным слагаемым. В противном случае используются различные модификации МНК.
Коэффициент уравнения называется идентифицируемым, если его можно вычислить на основе приведенных коэффициентов, причем точно идентифицируемым, если он единственный, и сверхидентифицируемым, если он имеет несколько разных оценок. В противном случае он называется неидентифицируемым.
Какое-либо структурное уравнение является идентифицируемым, если идентифицируемы все его коэффициенты. Если хотя бы один структурный коэффициент неидентифицируем, то и все уравнение является неидентифицируемым.
Модель считается идентифицируемой, если каждое ее уравнение идентифицируемо. Если хотя бы одно из уравнений системы неидентифицируемо, то и вся модель неидентифицируема.
В общем случае отдельное структурное уравнение системы является идентифицируемым, если имеется достаточное количество экзогенных (внешних) переменных (не включенных в само уравнение), которые можно использовать в качестве инструментальных для всех эндогенных объясняющих переменных уравнения.
Пусть 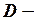 число экзогенных переменных, не включенных в уравнение, но присутствующих в системе; а
число экзогенных переменных, не включенных в уравнение, но присутствующих в системе; а 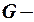 число эндогенных переменных уравнения.
число эндогенных переменных уравнения.
Уравнение структурной модели может быть идентифицируемо, если выполняется порядковое условие, т.е. число не включенных в него объясняющих экзогенных переменных не меньше числа включенных в него эндогенных переменных:
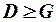 .
.
Порядковое условие является необходимым, но недостаточным для идентификации. В частности:
если 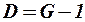 , то уравнение точно идентифицируемо;
, то уравнение точно идентифицируемо;
если 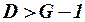 , то уравнение сверхидентифицируемо;
, то уравнение сверхидентифицируемо;
если 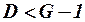 , то уравнение идентифицируемо.
, то уравнение идентифицируемо.
4.8. Рекомендации к применению методов оценивания
Приступать к оцениванию того или иного уравнения системы одновременных уравнений необходимо после того, как с помощью метода инструментальных переменных установлена его идентифицируемость.
Для решения задачи по определению параметров точно идентифицируемогоуравнения применяется косвенный метод наименьших квадратов (КМНК), а для решения задачи по определению параметров сверхидентифицируемогоуравнения – двухшаговый метод наименьших квадратов (ДМНК).
МетодКМНКвключает в себя следующиеэтапы:
1. Структурная (исходная) модель преобразуется в приведенную форму.
2. Для каждого приведенного уравнения обычным методом МНК определяются приведенные коэффициенты.
3. Оценки приведенных коэффициентов пересчитываются в оценки параметров структурных уравнений.
МетодДМНКвключает в себя следующиеэтапы:
1. На основе приведенной формы модели для сверхидентифицируемого уравнения получают теоретические (расчетные) значения эндогенных переменных, содержащихся в правой части уравнения.
2. Подставляя теоретические значения эндогенных переменных (вместо их фактических значений) в сверхидентифицируемое уравнение, с помощью обычного метода МНК определяют структурные коэффициенты этого уравнения.
Метод получил названиедвухшагового, так как метод МНК используется дважды: при нахождении теоретических значений эндогенных переменных из приведенной формы модели и при определении структурных коэффициентов по теоретическим значениям эндогенных переменных и исходным данным экзогенных переменных.
Трехшаговый метод наименьших квадратов (ТМНК) применяют при оценивании параметров всей системы уравнений в целом, если переменные, объясняемые в одном уравнении, в другом выступают в роли объясняющих. Например, в модели спроса и предложения, где, с одной стороны, спрос и предложение определяются рыночной ценой, а с другой – предложение должно быть равно спросу. При расчете параметров таких моделей учитывается вся система соотношений.
Алгоритм данного метода реализуется в три этапа. На первых двух этапах используется двухшаговый метод наименьших квадратов (ДМНК) для определения обычных коэффициентов регрессии.
После этого нужно увязать все уравнения системы между собой. В качестве меры устранения корреляции случайных членов используется матрица ковариаций ошибок моделей. Чтобы оценить, насколько несвязанными получаются уравнения спроса и предложения при расчете их отдельно, на последующем этапе при очередном счете коэффициентов регрессии учитывается матрица ковариаций ошибок регрессионных уравнений модели. Таким приемом достигается взаимосвязанность всей системы уравнений.
