Обратная задача теории погрешностей

На практике очень часто необходимо уметь решать обратную задачу: каковы должны быть абсолютные погрешности аргументов функции, чтобы абсолютная погрешность функции не превышала заданной величины.

Пусть величина предельной абсолютной погрешности 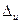задана.

Тогда .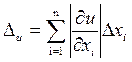

Предполагая, что все слагаемые равны между собой, будем иметь:

.

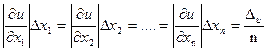Отсюда .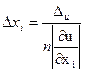

В случае, когда предельная абсолютная погрешность всех аргументов 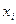одна и та же, то:

; .

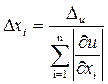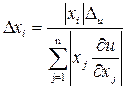7.1. Радиус основания цилиндра 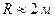; высота цилиндра 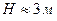. С какими абсолютными погрешностями нужно определить R и Н, чтобы объем цилиндра V можно было вычислить с точностью до 0,1 м ?

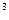Решение.

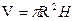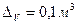Объем вычисляется по формуле и . Подставляя все исходные данные, приближенно получим:

; ; .

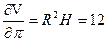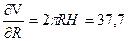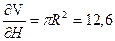Отсюда, т. к. п = 3, то, воспользовавшись формулой для вычисления погреш­ности функции, зависящей от трех переменных:

,

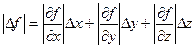Будем иметь:

; ;

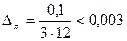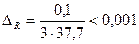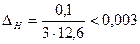
ТаблицаПогрешности значений элементарных функций.

8. Задания к лабораторной работе № 1:

8.1. Задания (самостоятельно).Найти предельные абсолютные и относительные погрешности чисел, если они имеют только верные цифры (таблица вариантов задания).

а) в строгом смысле; б) в широком смысле.

Таблица. Варианты заданий для выполнения самостоятельной работы

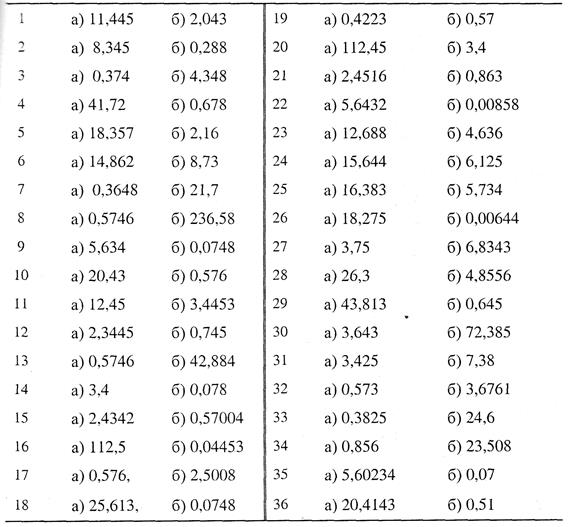
8.2. Задание для самостоятельной работы. Число х (табл.), все цифры которого верны в строгом смысле, округлить до трех значащих цифр. Для полученного результата 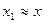вычислить границы абсолютной и относительной погрешностей. В записи числа 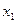, указать количество верных цифр по абсолютной и относительной погрешности.

Таблица. Варианты заданий для выполнения самостоятельной работы

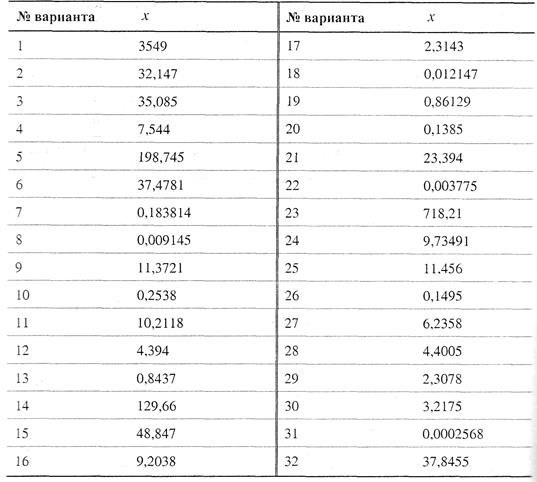
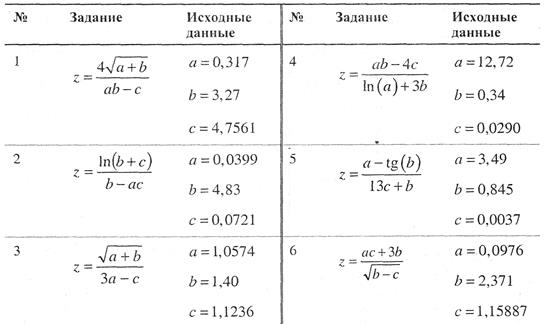
8.3. Вычислить значение величины z (табл) при заданных значениях чисел а , b и с используя систематический учет абсолютных погрешностей после каждой операции, а также с помощью метода границ. Найти абсолютную и относительную погрешности z и определить по ним количество верных цифр в z, если цифры а , b и с верны в строгом смысле.

Таблица. Варианты заданий для выполнения самостоятельной работы

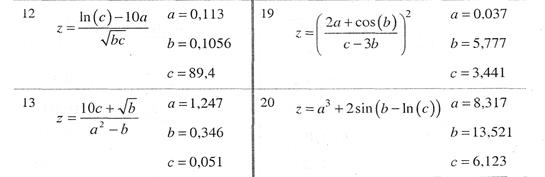
8.4. Решить следующие задачи, используя метод границ.

8.4.1. Длина воздушной трассы между двумя пунктами равна S км. Самолет преодолевает это расстояние за время t ч. Определить границы средней скорости самолета, если: ; .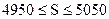

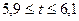8.4.2. Электроплитка рассчитана на напряжение 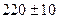В. Найти сопротивление спирали электроплитки, если известно, что через нее должен пройти ток 5±0,1 А.

8.4.3. Медный брусок имеет объем V м 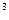( 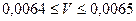). Найти его массу, если плотность меди 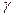кг/м 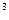составляет .

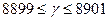8.5. Решить следующие задачи, используя общую формулу погрешности.

8.5.1. Удельное электрическое сопротивление 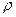металла круглого провода длиной l м с поперечным сечением d мм и сопротивлением R Ом определяется по формуле: 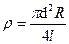. Найти 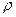, если: l=12,50 ±0,01 м, d=2,00±0,01 мм, R=0,068±0,0005 Ом, 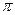=3,141 ±0,001. Определить относительную погрешность .

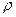8.5.2. Вертикальный цилиндрический резервуар наполнен жидкостью. Определить время, необходимое для опорожнения резервуара через круглое отверстие в дне. Диаметр резервуара D=1±0,01м, высота уровня жидкости H=2±0,02м, диаметр отверстия дна d=0,03±0,001м, коэффициент расхода 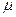=0,6 ±0,02. Расчет (в секундах) ведется по формуле: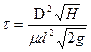

8.6.Решить следующие задачи, используя обратную задачу теории погрешностей:

8.6.1. С какой точностью надо измерить радиус круга R = 30,5 см и каким количеством значащих цифр следует ограничиться для числа 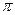, чтобы площадь круга была известна с точностью до 0,1%?

8.6.2. Длина сторон прямоугольника равны 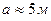, 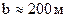. Какова допус­тимая предельная абсолютная погрешность при измерении этих величин одинаковая для обеих сторон, чтобы площадь S прямоугольника можно было определить с предельной абсолютной погрешностью ?

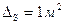Вопросы по теме

1. Что такое абсолютная и относительная погрешности?

2. Как классифицируются виды ошибок?

3. Что значит цифра, верная в строгом, широком смыслах?

4. Как находится погрешность округленного числа?

5. Как определить количество верных цифр по относительной погрешности приближенного числа?

6. Как распространяются абсолютная и относительная погрешности в арифметических действиях?

7. Как осуществить оценку погрешности значений элементарных функций?

8. Как формулируется обратная задача теории погрешности?

9. Каковы должны быть абсолютные погрешности аргументов функции, чтобы абсолютная погрешность функции не превышала заданной величины?

В каких случаях используется метод границ?