Пример 4.1. Найти коэффициент растяжения k и угол поворота a для отображения f (z) в точке , ,.

Решение . Функция 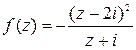представляет из себя отношение двух полиномов. Поэтому она голоморфна всюду в С, за исключением точки, в которой знаменатель обращается в ноль – это точка z = – i. Значит в точке 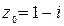, исследуемая функция имеет производную. Найдем ее.

; .

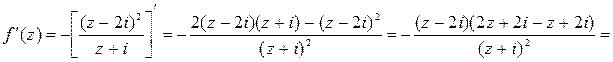
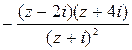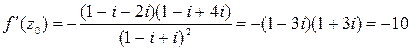Следовательно, 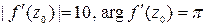. Поэтому коэффициент растяжения будет равен 10 а угол поворота p.

Пример 4.2. Найти Является ли функция w=f(z)=f(x+iy) дифференцируемой в смысле R² по переменным x, y , и дифференцируемой в смысле C по переменной z? Опишите области дифференцируемости

Решение . Представим заданную функцию w = f(z), где z = x + iy в виде

w = u(x, y) + iv(x, y). Проверим ее на дифференцируемость и аналитичность. В нашем случае w = f(z) = e^{1- iz}. Определим вещественную и мнимую составляющие нашей функции. Для этого подставим число z = x + iy в выражение нашей функции и проведем необходимые действия, учитывая, что i² = –1.

Используем обозначение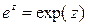

f(z) = e^{1- i(x + iy)} = e^{1- ix + y} = e^{1+ y - ix}

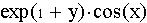+i( )

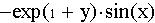Следовательно, вещественная и мнимая части функции f(z) имеют вид

Re(f(z)) = u(x, y) =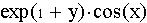

Im(f(z)) = v(x, y) =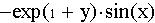

Теперь найдем всевозможные частные производные вещественной и мнимой частей нашей функции.

, ,

, .

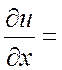
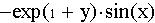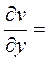
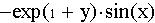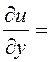
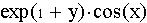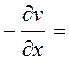
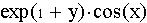Таким образом условия Коши-Римана

,

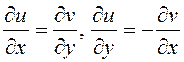для функции f(z) выполняются для всех точек комплексной плоскости С. Значить функции f(z) комплексно дифференцируема во всей комплексной плоскости С А так как С является открытым и связным множеством, т.е. областью, то следовательно всюду в С функция f(z) аналитична.

Вычисление производной функции f(z), с учетом этих условий можно провести по любой из формул

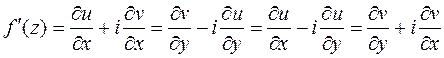
В нашем случае

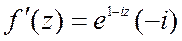
Физические приложения

Так как вещественная часть u(x,y) аналитической функции 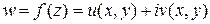есть функция гармоническая, то, как известно из курса векторного анализа, она может быть представлена как потенциал плоского поля. Следовательно, уравнение u(x,y) = c – const есть уравнение линий равного потенциала (эквипотенциальных линий). Нетрудно показать, что семейство v(x,y) = c – const, где v(x,y) – мнимая часть аналитической функции, есть семейство кривых, ортогональных линиям u(x,y) = c . Но тогда v(x,y) = c–const есть силовые линии поля. Таким образом, всякая аналитическая функция 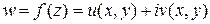дает картину плоского поля, электрического или магнитного, гидродинамического или теплового. Эта функция и называется, обычно комплексным потенциалом или характеристической функцией данного поля. В случае электрического или магнитного поля, если u(x,y) = c – const есть уравнение линий равного потенциала, то v(x,y) = c – const есть силовые линии поля. Напряженность E поля равна 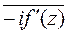, т.е.|E|=|f`(z)| 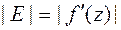, а Arg E = – (p/2 + (Argf`(z)). Если поле гидродинамическое и u(x,y) = const есть линии равного потенциала скорости, то v(x,y) = const – есть линии тока или траектории частиц жидкости. Величина скорости |V| =|f`(z)| , а направление скорости образует с положительным направлением оси Ох угол равный –argf`(z) В случае теплового поля, если u(x,y) =const есть изотермы, то v(x,y)=const есть линии теплового потока.

Пример 5.1. По заданному комплексному потенциалу плоского теплового поля 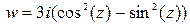найти изотермы, линии теплового потока и определить величину скорости потока.

Решение. Найдем реальную, мнимую части и модуль данного комплексного потенциала теплового поля. Комплексный потенциал 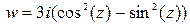с помощью тригонометрической формулы двойного угла, которая остается верной в комплексном анализе, можно привести к виду 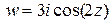. На основании определения комплексной функции косинус получим:

.

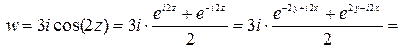
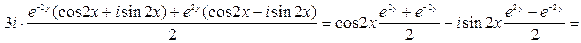
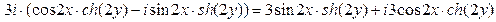
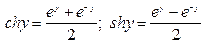
Во второй строке использовалась формулой Эйлера 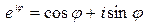. В третьей – определением гиперболических функций синуса и косинуса

.

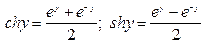Поэтому реальная часть комплексного потенциала

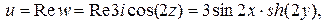
а мнимая

.

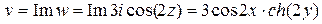Следовательно, модуль комплексного потенциала

.

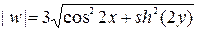В случае теплового поля, 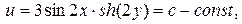–есть изотермы, – есть линии теплового потока.

Величина скорости |V| теплового потока совпадает с модулем производной комплексного потенциала теплового поля

.

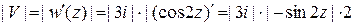Пользуясь формулой 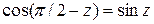и формулой для модуля w получим:

.
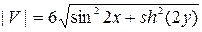