Сновные понятия теории вероятностей.
1.2. Алгебра событий
1. Возникновение или преднамеренное создание определенного комплекса условий S, результатом которого является тот или иной исход, называется …
| + | Испытанием | + | Опытом |
| - | Событием | - | Сочетанием |
| - | Вероятностью | + | Экспериментом |
2. Рассмотрим испытание: подбрасывается игральная кость. События: А – выпало 3 очка и В – выпало нечетное число очков являются:
| - | Несовместными | - | Равновозможными |
| + | Совместными | - | Единственно возможными |
| - | Противоположными |
3.Результатом операции суммы двух событий С = А + В является:
- А влечет за собой событие В;
+ произошло хотя бы одно из двух событий А или В;
- совместно осуществились события А и В.
4 . Выберите неверное утверждение:
- событие, противоположное достоверному, является невозможным;
- сумма вероятностей двух противоположных событий равна единице;
- если два события единственно возможны и несовместны, то они называются противоположными;
+ вероятность появления одного из противоположных событий всегда
больше вероятности другого.
5. Эксперимент состоит в подбрасывании один раз правильной шестигранной игральной кости. События А={выпало число очков больше трех}; В ={выпало четное число очков}. Тогда множество, соответствующее событию А+В, есть:
- А+В = {6};
- А+В = {4; 6};
+ А+В = {2; 4; 5; 6};
- А+В = {3; 4; 5; 6}.
6. Эксперимент состоит в подбрасывании один раз правильной шестигранной игральной кости. При каких событиях А, В верно: А влечет за собой В ?
- А = {выпало нечетное число очков}, B ={выпало число 3};
+ А = {выпало число 2}, B = {выпало четное число очков};
- А = {выпало число 6}, B = {выпало число очков, меньше 6}.
7. Взятая наудачу деталь может оказаться либо первого (событие А), либо второго (событие В), либо третьего (событие С) сорта. Что представляет
собой событие: 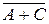 ?
?
- {деталь первого или третьего сорта};
+ {деталь второго сорта};
- {деталь первого и третьего сорта}.
8. Заданы множества А = {1, 3, 4}, В = {2, 3, 1, 4}, тогда для них будет неверным утверждением
- множество А есть подмножество множества В;
- множества А, В пересекаются;
- множество А не равно множеству В;
+ А и В не имеют общих элементов.
9. Известно, что Р (А) = 0,65 тогда вероятность противоположного события равна …
Ответ: 0,35.
10. Установите соответствие между событиями и вероятностями, с которыми эти события произойдут:
| А) | При подбрасывании игральной кости выпадет число очков, большее 4 | 1) | 1/3 |
| В) | При подбрасывании монеты выпадет герб | 2) | 1/2 |
| С) | Из колоды карт (36 штук) достали туза | 3) | 1/9 |
| 4) | 1/4 |
11. Установите соответствие между событиями и вероятностями, с которыми эти события произойдут:
| А) | При подбрасывании игральной кости выпадет число очков, меньшее 4 | 1) | 0,5 |
| В) | Из урны, в которой 6 белых и 4 черных шара, наугад достали белый шар | 2) | 0,6 |
| С) | Из колоды карт (36 штук) достали карту бубновой масти | 3) | 0,25 |
| 4) | 0,4 |
12. Установите соответствие между событиями и вероятностями, с которыми эти события произойдут:
| А) | При подбрасывании игральной кости выпадет число очков, кратное 3 | 1) | 1/3 |
| В) | Из урны, в которой 6 белых и 4 черных шара, наугад достали черный шар | 2) | 0,4 |
| С) | Из колоды карт (36 штук) достали пиковую даму | 3) | 1/36 |
| 4) | 0,6 |
13. Установите соответствие:
| А) | Число размещений из n по m | 1) | 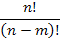 |
| В) | Число перестановок | 2) | 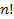 |
| С) | Число сочетаний из n по m | 3) | 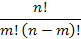 |
| 4) | 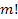 |
14. Игральный кубик подбрасывается один раз. Тогда вероятность того, что на верхней грани выпадет число очков больше трех, равно:
- 1/3;
+ 1/2;
- 2/3;
- 1/6.
15. В урне 5 белых, 3 черных, 4 красных шаров. Вероятность того, что из урны вынут белый или черный шар равна
- 1/4;
- 15/8;
+ 2/3;
-1/8.
16. В группе 7 юношей и 5 девушек. На конференцию выбирают трех cтудентов случайным образом (без возвращения). Вероятность того, что на конференцию поедут двое юношей и одна девушка, равна:
- 11/28;
+ 21/44;
- 21/110;
- 7/12.
17. В урне 6 белых и 4 черных шаров. Из урны вынимают два шара. Вероятность того, что оба шара черные, равна:
- 2/5;
+ 2/15;
- 1/4;
- 3/5.
18. Два стрелка производят по одному выстрелу. Вероятность попадания в цель для первого и второго стрелков равна 0,6 и 0,9 соответственно. Тогда вероятность того, что цель будет поражена, равна:
Ответ: 0,96
19. Количество перестановок в слове «ТВМС» равно:
Ответ: 24
20.Сколько различных двузначных чисел можно составить из пяти цифр 1, 2, 3, 4, 5, если все цифры в числе разные?
Ответ: 20
21. Игральную кость бросают 5 раз. Вероятность того, что ровно 3 раза появится нечетная грань, равна:
- 1/32;
- 1/16;
+ 5/16.
- 3/16
22. Наивероятнейшее число годных деталей среди 15 проверенных отделом технического контроля, если вероятность того, что деталь стандартна, равна 0,7, равно….
Ответ: 11
23. Для устройства, состоящего из трех независимо работающих элементов с соответствующими вероятностями отказа элементов 0,1; 0,2; 0,05, достаточно, чтобы отказал хотя бы один элемент.

Тогда вероятность отказа равна:
+ 0,316;
- 0,35;
- 0,001.
- 0, 023
24. Количество трехзначных чисел, в записи которых нет цифр 5 и 6 равно:
- 296;
+ 448;
- 1024;
- 526.
25. Число m0 наступления события А в n независимых испытаниях, в каждом из которых вероятность появления события равна p, определяемое из неравенства: pn – q < m0 < pn + q, называется:
- наибольшее;
- оптимальное;
+ наивероятнейшее;
- невозможное;
- минимальное.
26. Потребитель может увидеть рекламу определенного товара по телевидению (событие А), на рекламном стенде (событие В) и прочесть в газете (событие С). Событие А + В + С означает:
- потребитель увидел все три вида рекламы;
- потребитель не увидел ни одного вида рекламы;
+ потребитель увидел хотя бы один вид рекламы;
- потребитель увидел ровно один вид рекламы;
- потребитель увидел рекламу по телевидению.
27. На пяти одинаковых карточках написаны буквы И, Л, О, С, Ч. Если перемешать их, и разложить наудачу в ряд две карточки, то вероятность р получить слово ИЛ равна ….
Ответ: 0,05
28. Если A и B – независимые события, то вероятность наступления хотя бы одного из двух событий A и B вычисляется по формуле:
- P(A·B) = P(A)·P(B),
+P(A+B) = P(A) + P(B),
- P(A·B) = P(A)·P(B)·P(A·B),
- P(A+B) = P(A) + P(B) + P(A·B),
- P(A·B) = P(A)P(B/A).
29. Сколькими способами можно составить список из пяти студентов? В ответ записать полученное число.
Ответ:120
30. Подбрасываются две игральные кости. Найти вероятность Р того, что сумма выпавших очков равна четырем. В ответ записать число 24P.
Ответ: 2
31. Партия из 10 телевизоров содержит 3 неисправных телевизора. Из этой партии выбираются наугад 2 телевизора. Найти вероятность Р того, что оба они будут неисправными. В ответ записать число 45 Р.
Ответ: 3
32. Данное предприятие в среднем выпускает 20 % продукции высшего сорта и 70 % продукции первого сорта. Найти вероятность Р того, что случайно взятое изделие этого предприятия будет высшего или первого сорта. В ответ записать число 30 Р.
Ответ: 27
33. Студентам нужно сдать 4 экзамена за 6 дней. Сколькими способами можно составить расписание сдачи экзаменов?
Ответ: 360
34. Вероятность того, что случайно выбранный водитель застрахует свой автомобиль, равна 0,6. Наивероятнейшее число водителей, застраховавших автомобиль, среди 100 равно…
Ответ: 60
35. Вероятность появления события А в каждом из 100 независимых испытаний равна 0,4. Найдите математическое ожидание и дисперсию случайной величины Х – числа появлений события А. В ответ запишите их сумму.
Ответ: 64
36. Вероятность появления события А в каждом из 100 независимых испытаний равна 0,4. Тогда математическое ожидание и дисперсия случайной величины Х – числа появлений события А соответственно равны:
+ 40; 24,
- 24; 40,
- 20; 60,
- 44; 24.
37. В группе из 20 студентов 4 отличника и 16 хорошистов. Вероятности успешной сдачи сессии для них соответственно равны 0,9 и 0,65. Вероятность того, что наугад выбранный студент успешно сдаст сессию равна…
Ответ: 0,7
38. На плоскости нарисованы две концентрические окружности, радиусы которых 6 и 12 см соответственно. Вероятность того, что точка брошенная наудачу в большой круг, попадет в кольцо, образованное указанными окружностями равна:
- 0,50;
- 0,65;
- 0,12;
+ 0,75;
- 0,60.
39. На плоскости нарисованы две концентрические окружности, радиусы которых 6 и 12 см соответственно. Вероятность того, что точка брошенная наудачу в большой круг, попадет в кольцо, образованное указанными окружностями равна…
Ответ: 0,75
40. Опыт состоит в том, что стрелок производит 3 выстрела по мишени. Событие AK - «попадание в мишень при k-ом выстреле (k = 1, 2, 3). Выберите правильное выражение для обозначения события «хотя бы одно попадание в цель»:
- A1;
+ A1 + A2 +A3;
- 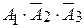 ;
;
- 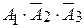 +
+ 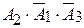 +
+ 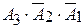 .
.
41. На сборку попадают детали с двух автоматов: 80 % из первого и 20 % из второго. Первый автомат дает 10 % брака, второй – 5 % брака. Вероятность попадания на сборку доброкачественной детали:
- 0,90;
- 0,09;
+ 0,91;
- 0,85;
- 0,15.
42. Некто купил два билета. Вероятность выигрыша хотя бы по одному билету равна 0,19, а вероятность выигрыша по одному лотерейному билету равна…
Ответ: 0,1
43. Вероятность посещения магазина № 1 равна 0,6, а магазина № 2 – 0,4. Вероятность покупки при посещении магазина № 1 равна 0,7, а магазина № 2 – 0,2. Вероятность покупки равна…
Ответ: 0,5
44. После бури на участке между 40-м и 70-м километрами телефонной линии произошел обрыв провода. Вероятность Р того, что разрыв произошел между 50-м и 55-м километрами равна…. (В ответ записать 60Р)
Ответ: 10
45. Партия деталей изготовлена двумя рабочими. Первый рабочий изготовил 32 всех деталей, а второй – 31. Вероятность брака для первого рабочего составляет 1%, а для второго – 10%. На контроль взяли одну деталь. Получено, что вероятность (в процентах) того, что она бракованная равна…
Ответ: 4
46. Пусть А, В, С – три произвольных события. Установить соответствия выражений для событий, состоящих в том, что из А, В, С:
1) произошло только А; a) 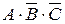
2) произошло А и В, но С не произошло; б) 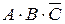
3) все три события произошли; в) 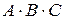
4) произошло два и только два события; г) 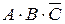 +
+ 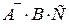 +
+ 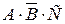
д) 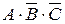 +
+ 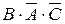 +
+ 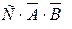
47. Вероятность того, что в течение одной смены возникнет неполадка станка, равна р. Вероятность того, что не произойдет ни одной неполадки за три смены равна:
- 3р;
- 3(1– р);
- p3;
- 1/3 p;
+ (1- р)3
48. При классическом определении вероятность события определяется равенством …
+ Р (А) = m/n
- Р (А) = n/m
- Р (А) = n/m2
- Р (А) = 1/n
49. Среди тридцати деталей, каждая из которых могла быть утеряна, было 10 нестандартных. Вероятность того, что утеряна нестандартная деталь, равна…
+ 1/3
- 0,3
- 3,0
- 1/5
50. Набирая номер телефона, абонент забыл последние три цифры и, помня, что эти цифры различны, набрал их наудачу. Вероятность того, что набраны нужные цифры, вычисляется по формуле…
+ 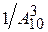
- 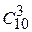
- 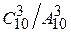
- 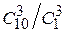
51. Вероятность появления одного из двух несовместных событий, безразлично какого, вычисляется по уравнению…
+ 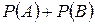
- 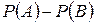
- 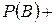
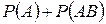
- 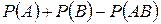
52. Событие, состоящее из элементарных событий, принадлежащих хотя бы одному из событий А или В, обозначается …
+ 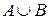
- 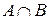
- 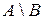
- 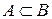
53. Событие состоящее из элементарных событий, принадлежащих одновременно А и В, обозначается…
+ 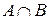
- 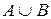
- 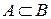
- 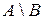
54. Событие, состоящее из элементарных событий, принадлежащих А и не принадлежащих В, обозначается…
+ 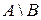
- 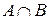
- 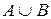
- 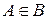
55. Если из наступления события А следует наступление события В, т.е. событие В есть следствие события А, то это записывается как…
+ 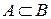
- 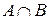
- 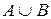
- 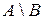
56. Вероятность достоверного события равна …
- 0
+ 1,0
- 0,5
- 1,0
57. Число комбинаций, состоящее из одних и тех же n различных элементов и отличающихся только порядком их расположения, вычисляется по формуле …
+ 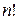
- 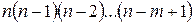
- 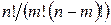
- 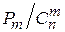
58. Число возможных размещений, составленных из n различных элементов по m элементов, которые отличаются либо составом элементов, либо их порядком вычисляется по формуле …
+ 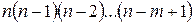
- 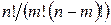
- 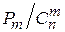
- 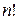
59. Число комбинаций, составленных из n различных элементов по m элементов, которые отличаются хотя бы одним из элементов, вычисляется по формуле …
- 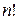
- 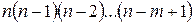
+ 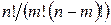
- 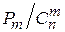
60. Количество трехзначных чисел, которое можно составить из цифр 1,2,3, если каждая цифра входит в изображение числа только один раз, вычисляют по формуле …
+ перестановок
- сочетаний
- размещений
- вероятности
61. Набирая номер телефона, абонент забыл одну цифру и набрал ее наудачу. Вероятность того, что найдена нужная цифра, равна …
+ 0,1
- 0,2
- 1/2
- 0/3.
62. Количество способов, которыми читатель может выбрать 4 книги из 11, равно:
| - | 353 | + | 330 | - | 341 | - | 326 |
63. Количество способов, которыми можно выбрать 5 экзаменационных билетов из 9, равно:
| - | 135 | + | 126 | - | 121 | - | 150 |
64. Количество способов, которыми можно сформировать экзаменационный билет из трех вопросов, если всего 25 вопросов, равно:
| - | 2500 | - | 75 | - | 575 | + | 2300 |
65. Количество способов, которыми можно выбрать двух дежурных из группы студентов в 20 человек, равно:
| - | 200 | + | 190 | - | 20! | - | 18! |
66. Количество способов, которыми могут 3 раза поразить мишень 10 стрелков, равно (каждый делает 1 выстрел):
| - | 10 | - | 30 | + | 120 | - | 720 |
67. Три стрелка делают по одному выстрелу по мишени. Событие 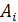 – попадание в мишень i-м стрелком. Событие
– попадание в мишень i-м стрелком. Событие 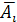 – промах i-м стрелком. Событие А – в мишень попали два раза представляется в виде операций над событиями как…
– промах i-м стрелком. Событие А – в мишень попали два раза представляется в виде операций над событиями как…
| - | 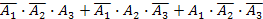 | - | 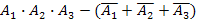 |
| - | 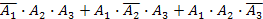 | + | 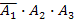 |
| - | 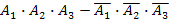 | - | 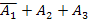 |
68. Укажите верные равенства (Æ - невозможное событие, W - достоверное событие):
| - | 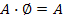 | + | 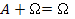 |
| - | 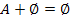 | - | 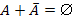 |
| + | 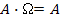 | - | 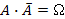 |
ДЕ 2. Основные теоремы теории вероятностей
2.1. Теоремы сложения и умножения
2.2. Повторение испытаний
1. Два стрелка производят по одному выстрелу. Вероятности попадания в цель для первого и второго стрелков равны 0,9 и 0,4 соответственно. Вероятность того, что в цель попадут оба стрелка, равна …
| - | 0,5 | - | 0,4 | - | 0,45 | + | 0,36 |
2. Сумма вероятностей событий А1, А2, … Аn, образующих полную группу, равна …
+ 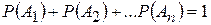
- 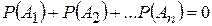
- 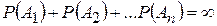
- 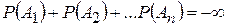
3. Сумма вероятностей противоположных событий равна …
+ 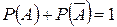
- 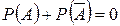
- 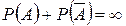
- 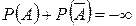
4. Вероятность совместного появления двух событий вычисляют по формуле …
+ 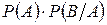
- 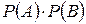
- 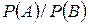
- 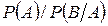
5. Теорема умножения для независимых событий имеет вид …
+ 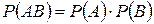
- 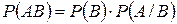
- 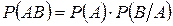
- 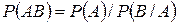
6. Вероятность появления хотя бы одного из трех независимых в совокупности событий равна …
+ 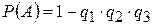
- 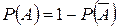
- 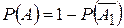
- 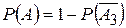
7. Вероятность появления хотя бы одного из двух совместных событий равна …
+ 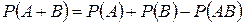
- 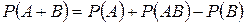
- 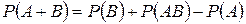
- 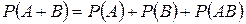
8. Вероятность попадания стрелком в цель равна 0,7. Сделано 25 выстрелов. Наивероятнейшее число попаданий в цель равно…
Ответ: 18
9. Монета брошена 3 раза. Тогда вероятность того, что "герб" выпадет ровно 2 раза, равна …
+ 3/8
- 3/4
- 1/8
- 2/3
10. Количество способов выбора стартовой шестерки из восьми игроков волейбольной команды равно …
- 113
+ 28
- 720
- 56
11. Из ящика, где находится 15 деталей, пронумерованных от 1 до15, требуется вынуть 3 детали. Тогда количество всевозможных комбинаций номеров вынутых деталей равно …
- 15!/12!
+ 15!/3!∙12!
- 15!
- 3!
12. Вероятность достоверного события равна …
- 0
+ 1,0
- 0,5
- 1,0
13. По оценкам экспертов вероятности банкротства для двух предприятий, производящих разнотипную продукцию равна 0,1 и 0,15. Тогда вероятность банкротства обоих предприятий равна …
- 0,15
+ 0,015
- 0,25
- 0,765
14. По оценкам экспертов вероятности банкротства для двух предприятий, производящих разнотипную продукцию равна 0,1 и 0,2. Тогда вероятность банкротства только одного предприятия равна …
+ 0,30
- 0,26
- 0,28
- 0,08
15. Вероятность попадания в мишень 0,8. Тогда наиболее вероятное число попаданий при 5 выстрелах равно …
- 3,8
- 4,8
+ 4,0
- 4,5
16. Брокерская фирма имеет дело с акциями и облигациями. Фирме полезно оценить вероятность того, что: лицо является держателем акций (событие А); лицо является держателем облигаций (событие В). Установите соответствие …
| А) | А+В | 1) | Лицо является держателем акций или облигаций |
| В) | А×В | 2) | Лицо является держателем акций и облигаций |
| С) | А – А×В | 3) | Лицо является держателем только акций |
| 4) | Лицо является держателем только облигаций |
17. Испытанием являются…
| + | Подбрасывание игральной кости |
| - | Выпадение орла при подбрасывании монеты |
| + | Вытаскивание шара из урны, в которой три черных и семь белых шаров |
| + | Выстрел по мишени |
| - | Увеличение курса доллара в следующем месяце |
18. Событием являются…
| + | Выигрыш по лотерейному билету |
| - | Вытаскивание игральной карты из колоды в 36 карт |
| - | Подбрасывание монеты |
| + | Выпадение двух очков при подбрасывании игральной кости |
| + | Промах при выстреле по мишени |
19. Рассмотрим испытание: подбрасывается игральная кость. Установите соответствие:
| А) | Достоверное событие | 1) | Выпало 3 очка |
| В) | Невозможное событие | 2) | Выпало больше 6 очков |
| 3) | Выпало меньше 6 очков | ||
| 4) | Выпало четное число очков |
20. Рассмотрим испытание: подбрасывается игральная кость.
События: А – выпало 3 очка и В – выпало нечетное число очков являются:
| - | Несовместными | - | Равновозможными |
| + | Совместными | - | Единственно возможными |
| - | Противоположными |
21. Рассмотрим испытание: из урны, содержащей 3 белых и 7 черных шаров, достают наугад один шар. События: А – достали белый шар и В – достали черный шар являются:
| - | Несовместными | - | Равновозможными |
| - | Совместными | - | Единственно возможными |
| + | Противоположными |
22. Несколько событий называются ____________, если в результате испытания обязательно должно произойти хотя бы одно из них.
| - | Несовместными | - | Равновозможными |
| - | Совместными | + | Единственно возможными |
| - | Противоположными |
23. События называются ____________, если в результате испытания по условиям симметрии ни одно из них не является объективно более возможным.
| - | Несовместными | + | Равновозможными |
| - | Совместными | - | Единственно возможными |
| - | Противоположными |
24. События называются ____________, если наступление одного из них исключает появление любого другого.
| + | Несовместными | - | Равновозможными |
| - | Совместными | - | Единственно возможными |
| - | Противоположными |
25. Несколько событий образуют полную группу событий, если они являются _____________ и __________________ исходами испытания.
| + | Несовместными | - | Равновозможными |
| - | Совместными | + | Единственно возможными |
| - | Противоположными | - | Достоверными |
26. Элементарными исходами (случаями, шансами) называются исходы некоторого испытания, если они ______ и ______.
| - | Несовместны | + | Равновозможны |
| - | Совместны | - | Единственно возможны |
| + | Образуют полную группу событий | - | Достоверны |
27. В квадрат со стороной 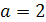 наудачу брошена точка. Вероятность того, что эта точка попадет в круг, вписанный в квадрат, равна …
наудачу брошена точка. Вероятность того, что эта точка попадет в круг, вписанный в квадрат, равна …
Ответ: 0,785
28. На отрезке L длины 20 см помещен меньший отрезок l длины 5 см. Вероятность того, что точка, наудачу поставленная на больший отрезок, попадет также и на меньший отрезок, равна …
Ответ: 0,25
29.В урне 12 белых и 8 черных шаров. Вероятность того, что наудачу вынутый шар будет белым равна…
Ответ: 0,6
30. Равенство 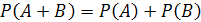 имеет место для ________ событий
имеет место для ________ событий
| - | Произвольных | - | Противоположных |
| + | Несовместных | - | Равновозможных |
| - | Совместных | - | Единственно возможных |
31. Равенство 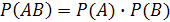 имеет место для __________ событий
имеет место для __________ событий
| - | Произвольных | - | Независимых |
| - | Несовместных | - | Зависимых |
| + | Совместных | - | Равновозможных |
32.Сумма вероятностей событий, образующих полную группу равна …
Ответ: единице; 1
33. Сумма вероятностей противоположных событий равна …
Ответ: единице; 1
34. В первом ящике 7 красных и 9 синих шаров, во втором – 4 красных и 11 синих. Из произвольного ящика достают один шар. Вероятность того, что он красный равна …
| - | 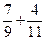 | - | 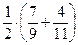 | + | 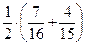 | - | 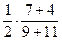 |
35. В первой урне 4 черных и 6 белых шаров. Во второй урне 3 белых и 7 черных шаров. Из наудачу взятой урны вынули один шар. Тогда вероятность того, что этот шар окажется белым, равна…
| + | 0,45 | - | 0,15 | - | 0,4 | - | 0,9 |
36. Событие А может наступить лишь при условии появления одного из двух несовместных событий 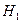 и
и 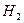 , образующих полную группу событий. Известны вероятность
, образующих полную группу событий. Известны вероятность 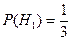 и условные вероятности
и условные вероятности 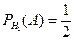 ,
, 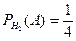 . Тогда вероятность
. Тогда вероятность 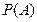 равна …
равна …
| - | 3/4 | - | 1/2 | + | 1/3 | - | 2/3 |
37. Формула полной вероятности имеет вид …
| + | 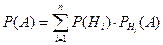 | - | 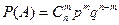 |
| - | 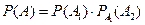 | - | 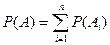 |
38. В первой урне 3 белых и 7 черных шаров. Во второй урне 1 белый и 9 черных шаров. Из наудачу взятой урны вынули один шар. Тогда вероятность того, что этот шар окажется черным, равна…
| + | 0,8 | - | 0,2 | - | 0,4 | - | 1,6 |
39. Формула Байеса имеет вид …
| - | 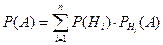 | - | 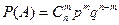 |
| - | 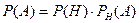 | + | 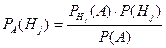 |
40. Если произошло событие А, которое может появиться только с одной из гипотез Н1, Н2, …, Hn образующих полную группу событий, то произвести количественную переоценку априорных (известных до испытания) вероятностей гипотез можно по …
| - | Формуле полной вероятности | - | Формуле Пуассона |
| + | Формуле Байеса | - | Формуле Муавра-Лапласа |
| - | Формуле Бернулли |
41. Установите соответствие:
| А) | Формула Бернулли | 1) | 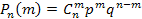 |
| В) | Формула Пуассона | 2) | 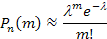 |
| C) | Локальная теорема Муавра-Лапласа | 3) | 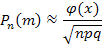 |
| 4) | 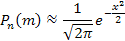 |
42. Установите соответствие между формулой и условием ее использования:
| А) | Формула Бернулли | 1) | 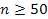 и и 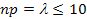 |
| В) | Формула Пуассона | 2) | 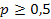 |
| C) | Локальная теорема Муавра-Лапласа | 3) | 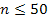 |
43. Событие А может наступить лишь при условии появления одного из трех несовместных событий 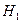 ,
, 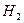 ,
, 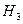 , образующих полную группу событий. Известны вероятности:
, образующих полную группу событий. Известны вероятности: 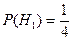 ,
, 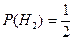 ,
, 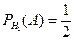 ,
, 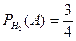 и
и 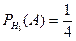 . Установите соответствие:
. Установите соответствие:
| А) | P(A) | 1) | 9/16 |
| В) | 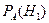 | 2) | 2/9 |
| C) | 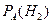 | 3) | 2/3 |
| D) | 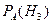 | 4) | 1/9 |
| 5) | 7/16 | ||
| 6) | 1/3 |
44. Стрелок стреляет по мишени 5 раз. Вероятность попадания в мишень при каждом выстреле постоянна. Вероятность того, что стрелок попадет по мишени не менее двух раз, равна…
| - | 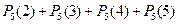 | - |  |
| - | 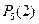 | - | 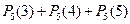 |
| - | 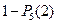 | + | 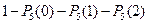 |
45. В ходе проверки аудитор случайным образом отбирает 60 счетов. В среднем 3% счетов содержат ошибки. Параметр l формулы Пуассона для вычисления вероятности того, что аудитор обнаружит два счета с ошибкой, равен …
Ответ: 1,8
46. Телефонная станция обслуживает 1000 абонентов. Вероятность позвонить любому абоненту в течение часа равна 0,001. Вероятность того, что в течение часа позвонят точно 3 абонента, приближенно равна…
| - | 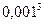 | - | 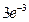 | - | 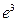 |
| + | 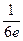 | - | 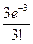 | - | 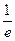 |
47. Укажите все условия, предъявляемые к последовательности независимых испытаний, называемой схемой Бернулли
| + | В каждом испытании может появиться только два исхода |
| - | Количество испытаний должно быть небольшим: n ≤ 50 |
| + | Вероятность успеха во всех испытаниях постоянна |
| - | В некоторых испытаниях может появиться больше двух исходов |
| + | Испытания являются независимыми |
48. Сделано 10 выстрелов по мишени. Вероятность попадания при одном выстреле 0,7. Наивероятнейшее число попаданий равно …
Ответ: 7
49. Установите соответствие между формулой и условием ее использования
| А) | Формула Бернулли | 1) | 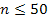 |
| В) | Формула Пуассона | 2) | 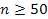 и и 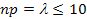 |
| С) | Локальная теорема Муавра-Лапласа | 3) | 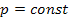 , , 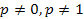 , , 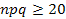 |
| 4) | 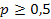 |
50. Формулой Пуассона целесообразно пользоваться, если …
| - | n = 500, p = 0,4 | + | n = 100, p = 0,02 | - | n = 3, p = 0,5 |
| + | n = 500, p = 0,003 | - | n = 100, p = 0,5 | - | n = 3, p = 0,05 |
51. Теоремами Муавра-Лапласа целесообразно пользоваться, если …
| + | n = 500, p = 0,4 | - | n = 100, p = 0,02 | - | n = 3, p = 0,5 |
| - | n = 500, p = 0,003 | + | n = 100, p = 0,5 | - | n = 3, p = 0,05 |
52. Монету подбросили 100 раз. Для определения вероятности того, что событие А – появление герба – наступит ровно 60 раз, целесообразно воспользоваться…
| - | Формулой полной вероятности |
| - | Формулой Байеса |
| - | Формулой Пуассона |
| + | Локальной теоремой Муавра-Лапласа |
| - | Интегральной теоремой Муавра-Лапласа |
53. Монету подбросили 100 раз. Для определения вероятности того, что событие А – появление герба – наступит не менее 60 раз и не более 80 раз, целесообразно воспользоваться…
| - | Формулой полной вероятности |
| - | Формулой Байеса |
| - | Формулой Пуассона |
| - | Локальной теоремой Муавра-Лапласа |
| + | Интегральной теоремой Муавра-Лапласа |
54. Вероятность появления события в каждом из 100 независимых испытаний постоянна и равна 0,8. Вероятность того, что событие появится не менее 60 раз и не более 88 раз, равна:
| - | 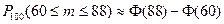 | + | 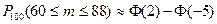 |
| - | 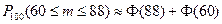 | - | 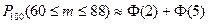 |
| - | 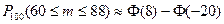 | - | 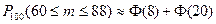 |
55. Вероятность появления события в каждом из 100 независимых испытаний постоянна и равна 0,8. Вероятность того, что событие появится точно 88 раз, равна:
| - | 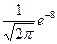 | - | 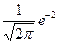 |
| + | j(2) | - | j(8) |
| - | 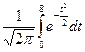 | - | 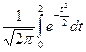 |
ДЕ 3. Случайные величины и законы их распределения
3.1. Дискретные случайные величины
3.2. Непрерывные случайные величины
1. Укажите дискретные случайные величины
| + | Число очков, выпавшее при подбрасывании игральной кости |
| - | Дальность полета артиллерийского снаряда |
| + | Количество произведенных выстрелов до первого попадания |
| - | Расход электроэнергии на предприятии за месяц |
| + | Оценка, полученная студентом на экзамене по теории вероятностей |
2. Укажите непрерывные случайные величины
| + | Температура воздуха |
| - | Количество произведенных выстрелов до первого попадания |
| + | Расход электроэнергии на предприятии за месяц |
| - | Рост студента |
| - | Оценка, полученная студентом на экзамене по теории вероятностей |
3. Вероятность появления события А в 10 независимых испытаниях, проводимых по схеме Бернулли, равна 0,8. Тогда дисперсия числа появлений этого события равна …
- 0,08
- 0,16
+ 1,6
- 8,0
4. Дискретная случайная величина задана законом распределения вероятностей:
| Х | -1 | ||
| Р | 0,1 | а | b |
Тогда ее математическое ожидание равно 3,3 если …
- a = 0,1, b = 0,9
+ a = 0,2, b = 0,7
- a = -0,1, b = 0,8
- a = -0,8, b = 0,1
5. Известно, что M(X) = 2, M(Y) = 3 и Х, Y – независимы. Установите соответствие:
| A) | M(3) | 1) | |
| B) | M(2X) | 2) | |
| C) | M(X+Y) | 3) | |
| D) | M(X–Y) | 4) | -1 |
| Е) | M(X×Y) | 5) | |
| 6) |
6. Известно 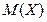 и
и 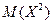 . Установите соответствие между данными
. Установите соответствие между данными 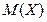 ,
, 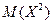 и соответствующим значением D(X):
и соответствующим значением D(X):
| А) | 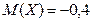 ; ; 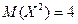 | 1) | 3,84 | |
| В) | 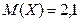 ; ; 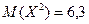 | 2) | 1,89 | |
| 3) | 4,4 | |||
| 4) | 4,2 |
7. Известно, что D(X) = 2, D(Y) = 3 и Х, Y – независимы. Установите соответствие:
| A) | D(3) | 1) | |
| B) | D(2X) | 2) | |
| C) | D(X+Y) | 3) | |
| D) | D(X–Y) | 4) | -1 |
| 5) |
8. Дискретная случайная величина Х задана законом распределения вероятностей
| Х | -5 | ||
| Р | 0,1 | 0,4 | 0,5 |
Установите соответствие:
| A) | Математическое ожидание | 1) | |
| B) | Мода | 2) | |
| C) | Медиана | 3) | |
| 4) | -5 |
9. Дискретная случайная величина Х задана законом распределения вероятностей
| Х | -1 | ||
| Р | 0,2 | 0,1 | 0,7 |
Значение 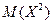 равно …
равно …
Ответ:0,9
10. В денежной лотерее выпущено 100 билетов. Разыгрывается пять выигрышей по 500 рублей, пять выигрышей по 400 рублей и десять выигрышей по 100 рублей. Математическое ожидание выигрыша по одному лотерейному билету равно…
Ответ: 55
11. Укажите справедливые утверждения для функции распределения случайной величины
| + | 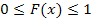 | - | 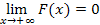 | + | 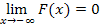 | - | 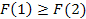 |
| - | 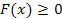 | + | 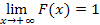 | - | 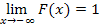 | + | 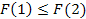 |
12. Укажите справедливые утверждения для непрерывной случайной величины (F(x) – интегральная функция распределения, j(x) – дифференциальная функция распределения)
