Поток событий. Простейший поток и его свойства
Под потоком событий в теории вероятностей понимается последовательность событий, происходящих одно за другим в какие-то моменты времени (например, поток вызовов на телефонной станции, поток покупателей в магазине и т.п.). События, образующие поток, в общем случае могут быть различными, но мы будем рассматривать лишь поток однородных событий, различающихся только моментами появления. Такой поток можно изобразить как последовательность точек на числовой оси, соответствующих моментам появления событий
| |||||||||
|
|
| |||||||
 | |||||||||
 | |||||||||
| |







|
| |
Поток событий называется регулярным, если события следуют одно за другим через строго определенные промежутки времени. Например, поток изделий на конвейере сборочного цеха (с постоянной скоростью движения) является регулярным. Такой поток сравнительно редко встречается в реальных системах, но представляет интерес как предельный случай.
Введем ряд определений.
10. Поток событий называется стационарным, если вероятность попадания того или иного числа событий на участок времени длиной τ (см. рис.) зависит только от длины участка и не зависит от того, где именно на оси 0t расположен этот участок. В частности, интенсивность стационарного потока есть величина постоянная: λ = λ(t).
Пример. Поток автомобилей на улице не является стационарным в течение суток, но этот поток можно считать стационарным в определенное время суток, например, в часы пик. В этом случае фактическое число проходящих автомобилей в единицу времени (например, в каждую минуту) может заметно различаться, но среднее их число постоянно и не будет зависеть от времени.
20. Поток событий называется потоком без последействия, если для любых двух непересекающихся участков времени число событий, попадающих в один из них, не зависит от числа событий, попадающих на другой.
Пример. Поток пассажиров, входящих в метро, практически не имеет последствий. А, например, поток покупателей, отходящих с покупками от прилавка, уже имеет последствия (хотя бы потому, что интервал времени между отдельными покупателями не может быть меньше, чем минимальное время обслуживания каждого из них).
30. Поток событий называется одинарным, если для любых непересекающихся участков времени число событий, попадающих на элементарный участок ∆t двух или более событий пренебрежимо мала по сравнению с вероятностью попадания одного события. Другими словами, поток одинарен, если события в нем появляются поодиночке, а не группами.
Пример. Поток поездов, подходящих к станции, одинарен, а поток вагонов не одинарен.
Поток событий называется простейшим (или стационарным пуассоновским), если он одновременно стационарен, одинарен и не имеет последствий.
Название «пуассоновский связано с тем, что при соблюдении условий 10 – 30 число событий, попадающих на любой фиксированный интервал времени, будет распределено по закону Пуассона.
Название «простейший» объясняется тем, что СМО с простейшим потоком имеет наиболее простое математическое описание. Регулярный поток не является простейшим, т.к. моменты появления событий в таком потоке жестко зафиксированы.
Простейший поток в качестве предельного возникает в теории случайных процессов столь же естественно, как в теории вероятностей нормальное распределение получается в качестве предельного для суммы случайных величин: при наложении (суперпозиции) достаточно большого числа n независимых, стационарных и одинарных потоков (сравнимых между собой по интенсивностям λi, i = 1,2, …, n), получается поток, близкий к простейшему с интенсивностью λ, равной сумме интенсивностей входящих потоков, т.е. 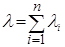 .
.
Рассмотрим на оси времени 0t простейший поток событий, как неограниченную последовательность случайных точек
 |
Пусть случайная величина Х выражает число событий (точек), попадающих на произвольный промежуток времени τ.
Теорема 1. В простейшем потоке с интенсивностью λ случайная величина Х(τ)распределена по закону Пуассона, т.е.
Р(Х= m) = pm(τ) = 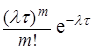 ,
,
математическое ожидание случайной величины равно ее дисперсии a = σ2 = λt.
Определение. Элементом вероятности появления события в простейшем потоке называется вероятность р1(Δt) появления события за элементарный (достаточно малый) промежуток времени Δt.
Теорема 2. Для элемента вероятности появления события справедлива следующая приближенная формула
р1(Δt) ≈ λΔt (Δt → 0).
Из теоремы 1 существует ряд следствий. Для лучшей обозримости все формулы из теорем 1 и 2, а также следствий из теоремы 1, характеризующие случайную величину Х, сведем в таблицу.
|
| Характеристика | Формула | |
| Интенсивность простейшего потока | λ | |
| Закон распределения Пуассона случайной величины Х | pm(τ) = 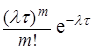 , (m = 0, 1, 2, …) , (m = 0, 1, 2, …) | |
| Вероятность того, что за промежуток времени τ в потоке не наступит ни одного события | p0(τ) = Р(Х= 0) = 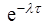 . . | |
| Вероятность того, что за промежуток времени τ в потоке наступит менееk(k=1,2,3…) событий | Р(Х<k) = 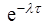 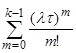 | |
| Вероятность того, что за промежуток времени τ в потоке наступит неменееk(k=1,2,3…) событий | Р(Х≥k) = 1- 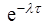 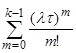 | |
| Вероятность того, что за промежуток времени τ в потоке наступит хотя бы одно событие | Р(Х≥1) = 1- 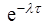 | |
| Элемент вероятности появления события | р1(Δt) ≈ λΔt (Δt → 0) | |
| Математическое ожидание случайной величины Х(τ) | М(Х(τ)) = а = λt | |
| Дисперсия случайной величины Х(τ) | D(Х(τ)) = λt | |
| Среднее квадратическое отклонение случайной величины Х(τ) | σ(Х(τ)) = 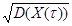 = = 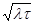 |
Другой важной характеристикой простейшего потока является непрерывная случайная величина Т – промежуток времени между двумя любыми соседними событиями потока. Аналитические выражения основных характеристик случайной величины Т даются в следующей теореме.
Теорема 3. В простейшем потоке с интенсивностью λ для случайной величины Т
1) Функция распределения F(t) = P(T < t) равна
F(t) = 1- 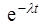 , t ≥ 0.
, t ≥ 0.
2) Плотность распределения равна
f(t) = 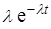 , t ≥ 0.
, t ≥ 0.
3) Математическое ожидание (средний интервал между двумя соседними событиями) равно среднему квадратическому отклонению и равно
М(Т) = σ(Т) = 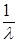 .
.
4) Дисперсия равна
D(Т) = 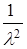 .
.
Приведенная теорема показывает, что случайная величина Т имеет показательный (экспоненциальный) закон распределения.
Свойством экспоненциального распределения является отсутствие последействия, которое состоит в том, что для любых неперекрывающихся участков времени число событий, попадающих на один из них, не зависит от числа событий, попадающих на другие.
Например, если сейчас 8.20 утра и некое событие имело место в 8.02 утра, то, в соответствии с экспоненциальным распределением, вероятность того, что следующее аналогичное событие произойдет в 8.29 утра, является лишь функцией интервала времени от 8.20 до 8.29, и не зависит от интервала времени, прошедшего с момента наступления последнего события (от 8.02 до 8.29).
Формально это свойство выглядит следующим образом.
Пусть время t наступления какого-либо события распределено по экспоненциальному закону с плотностью распределения f(t). Если S – время, прошедшее с момента наступления предыдущего события, то свойство отсутствия последействия выражается соотношением
P(t > T + S | t > S) = P(t > T).
Основанием для гипотезы об экспоненциальном распределении служит следующая теорема.
Теорема 4. Экспоненциальное распределение основано на трех аксиомах.
10. Если N(t) – число событий, произошедших на протяжении интервала времени (0, t), то вероятностный процесс, описывающий N(t), имеет независимые стационарные приращения: вероятность наступления события в интервале (T,T+S) зависит только от его длины S.
20. Вероятность того, что событие наступит на достаточно малом временном интервале, положительна, но меньше единицы.
30. На достаточно малом временном интервале h > 0 может осуществиться не более одного события, т.е. P(N(h) > 1) = 0.
