Тема. Обчислення площ плоских фігур за допомогою визначеного інтеграла. Розв’язування прикладних задач

Мета роботи: Навчитись обчислювати площі плоских фігур за допомогою визначеного інтегралу, розв’язувати різні прикладні задачі.

Наочне забезпечення та обладнання:

1. Інструкційні картки

2. Приклади задач

3. Роздаткові матеріали: опорні конспекти “Основні формули інтегрування”

4. Обчислювальні засоби: калькулятор.

Теоретичні відомості про правила інтегрування та застосування визначеного інтегралу

Формула Ньютона – Лейбніца.

Для обчислення визначеного інтеграла від функції 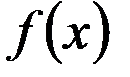в тому випадку, коли можна знайти відповідний невизначений інтеграл 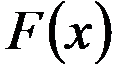, є формула Ньютона – Лейбніца: , тобто визначений інтеграл дорівнює різниці значень первісної при верхній і нижній межах інтегрування.

Застосування визначеного інтегралу до обчислення шляху за відомим законом зміни швидкості.

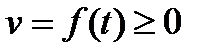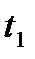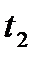Шлях, пройдений точкою при нерівномірному русі по прямій із змінною швидкістю за проміжок часу від до , обчислюють за формулою: .

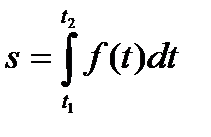Завдання 1. Швидкість руху точки змінюється за законом 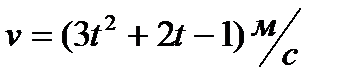. Знайдіть шлях, пройдений точкою за 10с від початку руху.

Обчислення площі плоскої фігури.

Площа криволінійної трапеції, обмеженої графіком функції 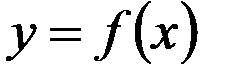, прямими 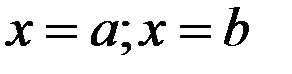, де 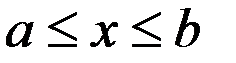та віссю 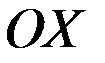обчислюється за формулою: .

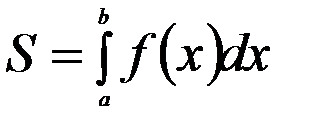Завдання 2. Обчислити площу фігури, обмеженої лініями: , .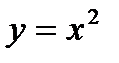

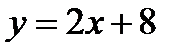Питання для самоконтролю знань, умінь.

1. Пояснити зміст визначеного інтеграла як границі інтегральної суми.

2. Властивості визначеного інтегралу:

· інтеграл суми функцій;

· винесення коефіцієнта за знак інтеграла;

· похідна від інтеграла;

· інтеграл, взятий на участках одного проміжку.

3. Вказати етапи розв’язування задачі на обчислення площі плоскої фігури за допомогою визначеного інтегралу.

Висновок.______________________________________________________________

Перевірив викладач ___________ Оцінка___________Дата___________

ТЕМА 7. ДИФЕРЕНЦІАЛЬНІ РІВНЯННЯ

ПРАКТИЧНА РОБОТА № 16

Тема. Роз’язування лінійних диференціальних рівнянь з відокремлюваними змінними. Задача Коші

Мета роботи: навчитись розв’язувати лінійні диференціальні рівняння з відокремлюваними змінними;знаходити їх загальні та часткові розв’язки.

Наочне забезпечення та обладнання:

1. Інструкційні картки

2. Приклади задач

3. Роздаткові матеріали: варіанти завдань

4. Обчислювальні засоби: калькулятор.