Подъемная сила

Рассмотрим обтекание двояковыпуклого симметричного профиля идеальным газом (см. рис. 25). Профиль считается симметричным, если он симметричен относительно хорды. Пусть он сначала установлен под углом атаки a = 0. В данном случае угол атаки равен углу между вектором скорости набегающего потока 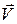и хордой профиля.

Рис. 25. Обтекание симметричного профиля при a = 0

(без образования подъемной силы)

У носка профиля в передней критической точке A происходит полное торможение потока, статическое давление в этой точке максимально и равно полному давлению. Далее поток разделяется на два: один обтекает верхнюю поверхность профиля, другой – нижнюю. У задней кромки профиля потоки опять сливаются в задней критической точке B. В точке B так же, как и в точке A скорость потока равна 0, потому что здесь сходятся линии тока, идущие по верхней и нижней поверхностям профиля, а частица газа не может одновременно двигаться по двум направлениям. Следовательно, в точке B статическое давление так же, как и в точке A максимально и равно полному давлению. Но между точками A и B статическое давление отличается от полного давления. Это является следствием того, что в процессе движения от точки A к точке B площади поперечных сечений струек сначала уменьшаются, а потом растут. При этом в соответствии с уравнением неразрывности (10) скорость в струйках будет соответственно сначала расти, а затем падать. Из закона сохранения энергии в аэродинамике (см. уравнение Бернулли (16)) следует, что при увеличении скорости статическое давление уменьшается. Значит, от точки A до точки B на верхней и нижней поверхностях профиля будут располагаться зоны относительного разрежения. Поскольку мы рассматриваем симметричный профиль, то величины падения статического давления в этих зонах будут одинаковыми. Это значит, что в направлении, перпендикулярном вектору скорости набегающего потока, на профиль не будет воздействовать составляющая аэродинамической силы, названная выше подъемной.

Очевидно, что для того, чтобы получить подъемную силу нужно сделать профиль несимметричным или установить симметричный профиль под некоторым углом атаки a ¹ 0 (см. рис. 26).

Рассмотрим обтекание профиля потоком под углом атаки a > 0. В этом случае струйка, обтекающая профиль сверху, будет иметь большее сужение, чем струйка, обтекающая профиль снизу, а значит скорость в верхней струйке будет больше, чем в нижней (V_в > V_н). Это приведет к тому, что на верхней поверхности профиля статическое давление будет меньше, чем на нижней (p_в < p_н). Из-за этой разности образуется аэродинамическая подъемная сила, направленная вверх.

Рис. 26. Обтекание профилей с образованием подъемной силы

Естественно предположить, что чем больше угол атаки или вогнутость профиля, тем больше будет и подъемная сила. Рассмотрим вначале влияние угла атаки на подъемную силу симметричного профиля. В формуле подъемной силы (35) имеется коэффициент, который зависит от угла атаки – это коэффициент подъемной силы C_ya. График зависимости C_ya от a для симметричного и несимметричного профилей представлен на рис. 27, из которого видно, что при малых углах атаки коэффициент подъемной силы зависит от a линейно.

Рис. 27. Зависимость коэффициента подъемной силы от угла атаки

Если профиль имеет положительную относительную вогнутость, то кривая смещается плоскопараллельно вверх. Угол атаки, при котором C_ya = 0 обозначается a₀, в данном случае a₀ < 0. Легко видеть, что при одном и том же угле атаки профиль, имеющий большую относительную вогнутость, будет иметь больший коэффициент подъемной силы.

На больших углах атаки нарушается плавное обтекание профиля. Это происходит из-за влияния вязкости на движение частиц в пограничном слое. В процессе движения вдоль верхней поверхности профиля частицы воздуха будут терять скорость. На каком-то этапе им не хватит кинетической энергии, чтобы двигаться дальше вдоль поверхности. В итоге на некотором участке верхней поверхности профиля произойдет отрыв пограничного слоя. Это явление приводит к нарушению линейности зависимости . При увеличении угла атаки зона отрыва также будет увеличиваться, но коэффициент подъемной силы C_ya при этом продолжает расти и достигает своего максимального значения C_yamax. Угол атаки, который соответствует C_yamax называется критическим углом атаки a_кр (см. рис. 28). Величина критического угла атаки как правило не превышает 20°. При дальнейшем увеличении угла атаки отрыв потока достигнет интенсивности, при которой коэффициент подъемной силы будет резко падать.

Рис. 28. Соответствие максимального значения коэффициента подъемной

силы критическому углу атаки