Вопрос 7.1. Аддитивность определенного интеграла
Положим по определению, что
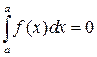
и
.
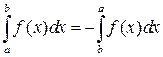Теорема 7.1. (Аддитивность определенного интеграла). Если c некоторое число, то
.
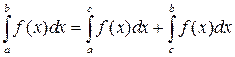при условии, что все указанные интегралы существуют.
Доказательство. Пусть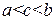 
и T такое разбиение, что c попадает на правый конец одно
го из отрезков разбиения. Тогда получаем
.
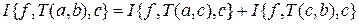Переходя к пределу при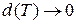 
, получим
.
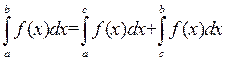Пусть теперь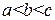 
. Тогда применяя свойство аддитивности к отрезку 
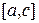, получим
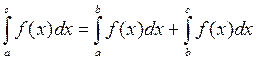
или
.
Меняя в последнем интеграле пределы интегрирования, получим
.
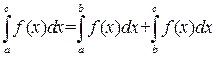Аналогично доказывается свойство аддитивности при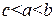 
.
Конец доказательства.
Вопрос 7.2. Основная формула интегрального исчисления (формула Ньютона - Лейбница).
Теорема 7.2. Если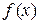 
непрерывна на отрезке 
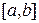, то 
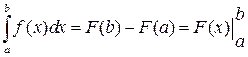, где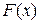 
любая первообразная функции .
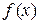Доказательство. Рассмотрим вспомогательную функцию
.
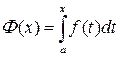Вычислим производную от функции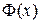 
.
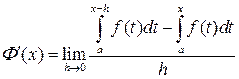Так как по свойству аддитивности
,
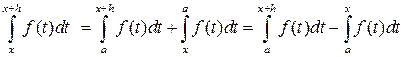то
,
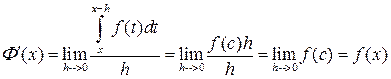где была использована теорема о среднем значении
.
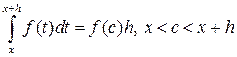Таким образом,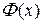 
есть первообразная для функции 
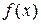. Так как в точке а 
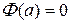, то
,
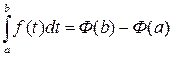но если 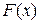является другой первообразной для функции 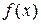, то 
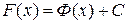и
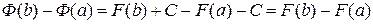
и
.
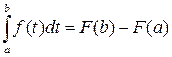Конец доказательства.
Замечание 7.1. Из доказательства теоремы следует, что если 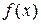непрерывна, то она имеет первообразную
.
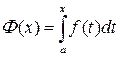Конец замечания.
Формула Ньютона-Лейбница сводит вычисление определенного интеграла к вычислению неопределенного интеграла.
Пример 7.1.
.
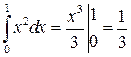Конец примера.
Вопрос 7.3. Замена переменных в определенном интеграле.
Теорема 7.3. Пусть 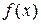непрерывная на отрезке 
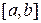функция, и 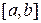есть множество значений некоторой функции 
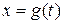, непрерывно дифференцируемой на отрезке 
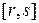, причем 
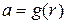и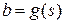 
, тогда справедлива формула замены переменной
.
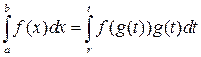Доказательство. Пусть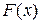 
первообразная для функции 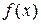. Тогда 
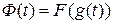есть первообразная для функции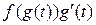 
.
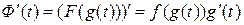По формуле Ньютона ‑ Лейбница
,
.
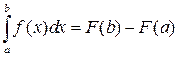Отсюда следует, что левые части формул равны между собой.
Конец доказательства.
Пример 7.2.
.
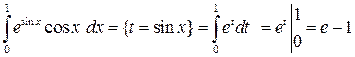Конец примера.
Вопрос 7.4. Интегрирование по частям в определенном интеграле.
Теорема 7.4. Пусть на отрезке 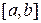заданы две дифференцируемые функци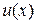и 
и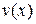 
с непрерывными производными. Тогда справедлива формула интегрирования по частям
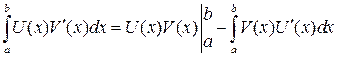
или
.
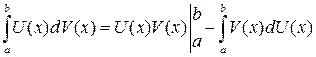Доказательство. Проинтегрируем левую и правую часть формулы дифференцирования произведения двух функций
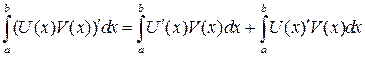
получим, после переноса, доказываемую теорему
.
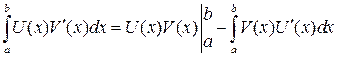Конец доказательства.
Метод интегрирования по частям используется для интегрирования тех же классов функций, что и в случае неопределенных интегралов.
Пример 7.3.
.
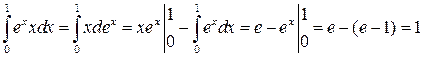Конец примера.