Гомоморфизм
Пусть  - группа и
- группа и 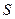 - другая группа или полугруппа. Пусть каждому элементу
- другая группа или полугруппа. Пусть каждому элементу 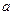 из
из  сопоставлен некоторый элемент из
сопоставлен некоторый элемент из 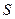 , т. е. задано отображение
, т. е. задано отображение  в
в 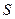 .
.
Определение. Отображение 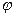 называется гомоморфным (или гомоморфизмом
называется гомоморфным (или гомоморфизмом  в
в 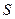 ), если произведению любых элементов из
), если произведению любых элементов из  соответствует произведение их образов, т. е.
соответствует произведение их образов, т. е. 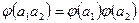 .
.
При этом не предполагается, что отображение является взаимно однозначным, т. е. различным элементам из  может соответствовать один и тот же элемент из
может соответствовать один и тот же элемент из 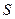 , а некоторые элементы из
, а некоторые элементы из 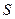 могут не являться образами каких-либо элементов из
могут не являться образами каких-либо элементов из  .
.
Лемма 1. Гомоморфизмом 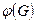 группы
группы  является группа. Образом единицы группы
является группа. Образом единицы группы  является единица образа и взаимно обратным элементам группы
является единица образа и взаимно обратным элементам группы  соответствуют взаимно обратные образы.
соответствуют взаимно обратные образы.
Доказательство. Так как 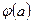 и
и 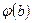 принадлежат
принадлежат 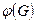 , то из равенства
, то из равенства 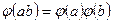 следует, что
следует, что 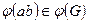 . Ассоциативность следует из ассоциативности в
. Ассоциативность следует из ассоциативности в  и
и 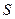 :
: 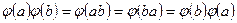 . Покажем, что есть левая единица для
. Покажем, что есть левая единица для 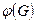 :
: 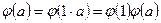 , т. е.
, т. е. 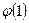 - левая единица в
- левая единица в 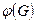 . Из равенства
. Из равенства 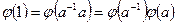 следует, что
следует, что 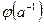 является левым обратным элементом для элемента
является левым обратным элементом для элемента 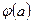 в
в 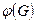 . Аналогично доказывается существование правого обратного элемента и правой единицы. Таким образом,
. Аналогично доказывается существование правого обратного элемента и правой единицы. Таким образом, 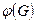 является группой.
является группой.
Замечание. Если 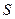 - полугруппа, а не группа, то
- полугруппа, а не группа, то 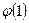 может не быть единицей для всей
может не быть единицей для всей 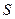 . Однако
. Однако 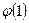 является единицей для
является единицей для 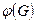 ,. Или для любой группы, содержащейся в
,. Или для любой группы, содержащейся в 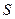 и содержащей
и содержащей 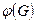 .
.
Пусть 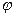 - гомоморфное отображение группы
- гомоморфное отображение группы  на группу
на группу 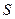 .
.
Определение. Множество всех элементов из  , имеющих один и тот же образ
, имеющих один и тот же образ 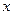 ,
, 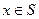 , называется полным прообразом элемента
, называется полным прообразом элемента 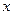 и обозначается
и обозначается 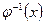 . Полный прообраз единицы группы
. Полный прообраз единицы группы 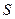 называется ядром гомоморфизма.
называется ядром гомоморфизма.
Лемма 2. Ядро гомоморфизма группы  на группу
на группу 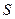 является полной нормальной подгруппой группы
является полной нормальной подгруппой группы  .
.
Доказательство. Пусть  - ядро гомоморфизма. Так как
- ядро гомоморфизма. Так как 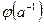 является обратным элементом для
является обратным элементом для 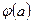 , то
, то 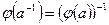 . Если
. Если 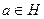 , то
, то 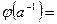
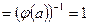 и, следовательно,
и, следовательно, 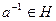 . Если
. Если 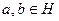 , то
, то 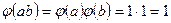 , т. е.
, т. е. 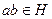 . Если
. Если 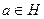 ,
, 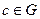 , то
, то 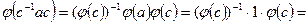
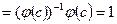 , поэтому
, поэтому 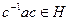 .
.
Лемма 3. В условиях леммы 2 полные прообразы элементов из 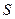 являются классами смежности по ядру гомоморфизма.
являются классами смежности по ядру гомоморфизма.
Доказательство. Если 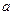 и
и 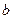 принадлежат одному классу смежности по
принадлежат одному классу смежности по  , то
, то 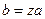 при
при 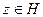 и
и 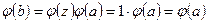 . Если
. Если 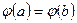 , то
, то 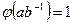 , поэтому
, поэтому 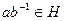 ,
, 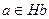 и
и 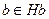 .
.
Теорема (первая теорема о гомоморфизмах). Гомоморфный образ группы изоморфен ее факторгруппе по ядру гомоморфизма
Доказательство. Между образами при гомоморфизме и элементами факторгруппы имеется взаимно однозначное соответствие согласно лемме 3. Оно сохраняется при умножении: 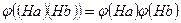 .
.
Отображение группы  на факторгруппу
на факторгруппу 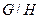 по нормальной подгруппе
по нормальной подгруппе  , заключающееся в том, что каждому элементу группы
, заключающееся в том, что каждому элементу группы  сопоставляется содержащий его класс смежности, есть гомоморфизм и его ядро совпадает с
сопоставляется содержащий его класс смежности, есть гомоморфизм и его ядро совпадает с  . Это следует из определения умножения классов смежности как элементов факторгруппы. Это гомоморфизм
. Это следует из определения умножения классов смежности как элементов факторгруппы. Это гомоморфизм  на
на 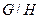 называется естественным гомоморфизмом. Поэтому первая теорема о гомоморфизме утверждает, что любой гомоморфизм в основном ( с точностью до изоморфизма) не отличается от естественного гомоморфизма группы на ее факторгруппу по ядру гомоморфизма.
называется естественным гомоморфизмом. Поэтому первая теорема о гомоморфизме утверждает, что любой гомоморфизм в основном ( с точностью до изоморфизма) не отличается от естественного гомоморфизма группы на ее факторгруппу по ядру гомоморфизма.
Пример. Пусть  - группа по умножению невырожденных квадратных матриц над полем
- группа по умножению невырожденных квадратных матриц над полем 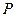 ,
, 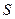 - полугруппа элементов поля
- полугруппа элементов поля 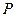 относительно умножения и
относительно умножения и 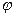 - отображение, ставящее в соответствие каждой матрице из
- отображение, ставящее в соответствие каждой матрице из  ее определитель. Это отображение является гомоморфизмом, т. к. определитель от произведения матриц равен произведению их определителей. Образ состоит из всех элементов поля
ее определитель. Это отображение является гомоморфизмом, т. к. определитель от произведения матриц равен произведению их определителей. Образ состоит из всех элементов поля 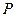 , кроме нуля. Любой элемент
, кроме нуля. Любой элемент 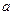 из
из 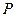 есть определитель матрицы, отличающейся от единичной тем, что на главной диагонали вместо одной единицы стоит число
есть определитель матрицы, отличающейся от единичной тем, что на главной диагонали вместо одной единицы стоит число 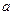 . Ядром отображения является группа матриц с определителем, равным единице, так что эта группа есть нормальная подгруппа группы невырожденных матриц. Классы смежности по ядру составляют матрицы, имеющие одинаковый определитель.
. Ядром отображения является группа матриц с определителем, равным единице, так что эта группа есть нормальная подгруппа группы невырожденных матриц. Классы смежности по ядру составляют матрицы, имеющие одинаковый определитель.
Лемма 4. Пусть  и
и 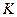 - подгруппы группы
- подгруппы группы  , причем
, причем  - нормальная подгруппа. Тогда
- нормальная подгруппа. Тогда 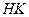 - подгруппа группы
- подгруппа группы  и
и 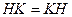 .
.
Доказательство. Пусть 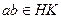 , причем
, причем 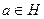 ,
, 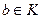 . Тогда
. Тогда 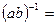
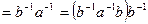 , причем
, причем 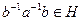 , т. к.
, т. к.  - нормальная подгруппа, и
- нормальная подгруппа, и 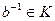 . Поэтому
. Поэтому 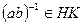 . Пусть
. Пусть 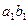 и
и 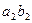 принадлежат
принадлежат 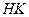 ,
, 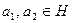 ,
, 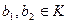 . Тогда
. Тогда 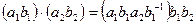 , где
, где 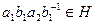 в силу нормальности
в силу нормальности  ,
, 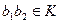 , следовательно,
, следовательно, 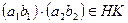 . Лемма доказана.
. Лемма доказана.
Теорема (вторая теорема о гомоморфизме). Пусть  и
и 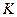 - подгруппы группы
- подгруппы группы  , причем
, причем  - нормальная подгруппа. Тогда факторгруппа
- нормальная подгруппа. Тогда факторгруппа 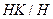 изоморфна факторгруппе
изоморфна факторгруппе 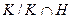 .
.
Доказательство. Рассмотрим какой-либо гомоморфизм 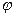 группы
группы  на группу
на группу 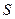 с ядром
с ядром  , например, естественный гомоморфизм группы
, например, естественный гомоморфизм группы  на
на 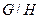 . Образы элементов подгруппы
. Образы элементов подгруппы 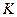 группы
группы  составят некоторую подгруппу
составят некоторую подгруппу 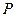 группы
группы 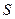 . Подгруппа
. Подгруппа 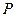 является гомоморфным образом подгруппы
является гомоморфным образом подгруппы 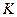 при отображении
при отображении 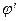 , совпадающим с
, совпадающим с 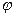 на
на 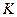 . Ядром отображения
. Ядром отображения 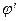 является пересечение
является пересечение 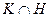 группы
группы 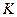 с ядром
с ядром  гомоморфизма
гомоморфизма 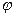 . Поэтому
. Поэтому 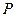 изоморфна
изоморфна 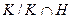 . С другой стороны, если
. С другой стороны, если 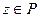 и является образом элемента
и является образом элемента 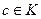 , то полный прообраз
, то полный прообраз 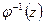 есть смежный класс
есть смежный класс 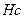 , и объединение всех этих прообразов есть подгруппа
, и объединение всех этих прообразов есть подгруппа 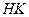 группы
группы  . Поэтому образ
. Поэтому образ 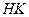 при гомоморфизме
при гомоморфизме 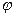 снова совпадает с
снова совпадает с 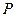 . Так как ядро
. Так как ядро  гомоморфизма
гомоморфизма 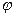 содержится в группе
содержится в группе 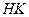 , группа
, группа 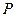 изоморфна
изоморфна 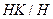 . Отсюда следует изоморфизм факторгрупп
. Отсюда следует изоморфизм факторгрупп 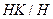 и
и 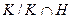 . Теорема доказана.
. Теорема доказана.
Пусть  - нормальная подгруппа группы
- нормальная подгруппа группы  ,
, 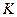 - какая-либо промежуточная подгруппа, т. е.
- какая-либо промежуточная подгруппа, т. е. 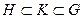 . Тогда
. Тогда  есть нормальная подгруппа для
есть нормальная подгруппа для 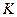 и имеет смысл факторгруппа
и имеет смысл факторгруппа 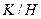 , которая является подгруппой группы
, которая является подгруппой группы 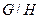 .
.
Теорема (третья теорема о гомоморфизме). Пусть 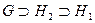 , где
, где 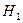 и
и 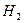 - нормальные подгруппы в группе
- нормальные подгруппы в группе  . Тогда
. Тогда 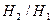 есть нормальная подгруппа группы
есть нормальная подгруппа группы 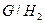 и
и 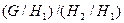 изоморфна
изоморфна 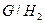 .
.
Эту теорему примем без доказательства.
