Закон Ома для участка цепи

Рассмотрим закон Ома для участка цепи, содержащего активные и пассивные элементы. Пусть на неразветвленном участке 1-3 сложной цепи (рис. 1.15), содержащей источник и потребитель энергии, протекает ток I.

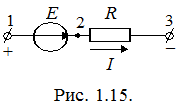Для определения потенциала любой точки электрической цепи необходимо произвольно задать потенциал какой-нибудь одной точки. Пусть для рассматриваемой схемы 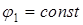. Потенциал точки 2 больше потенциала точки 1 на значение ЭДС: 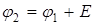. Ток I в любом пассивном элементе цепи направлен от точки с более высоким потенциалом до точки с более низким потенциалом. Поэтому потенциал точки 3 меньше потенциала точки 2, т.е. .

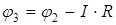Объединив эти две формулы, получаем:

(1.15)

Отсюда ток 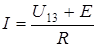(1.16)

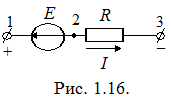Рассуждая аналогичным образом, можно получить выражение обобщенного закона Ома для случая противодействующего источника ЭДС:

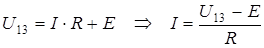(1.17)

Объединив эти две формулы в одну, получим:

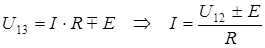, (1.18)

где верхний знак соответствует ветви с содействующим источником ЭДС, а нижний – с противодействующим. Выведенная формула представляет собой закон Ома для участка цепи с ЭДС или обобщенный закон Ома.

Если в результате расчета по формуле (1.16) ток получает отрицательное значение, это означает, что действительное направление тока противоположно выбранному направлению.

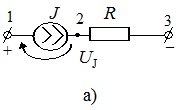
Обобщенный закон Ома можно вывести для ветви, содержащей источник тока (рис. 1.17).

Для содействующего (рис. 1.17, а) источника тока

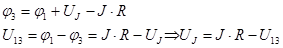
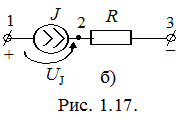
Для противодействующего (рис. 1.17, б) источника тока

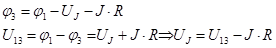
Объединенная форма обобщенного закона Ома для ветвей, содержащих источник тока:

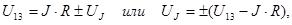(1.19)

где верхний знак соответствуют схеме, на которой U_J и J со направлены.

Первый закон Кирхгофа

В любом узле электрической цепи алгебраическая сумма токов равна нулю

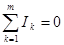(1.20)

где m – число ветвей подключенных к узлу.

При записи уравнений по первому закону Кирхгофа токи, направленные к узлу, берут со знаком «плюс», а токи, направленные от узла – со знаком «минус». Например, для узла а (см. рис. 1.2)

I−I₁−I₂=0.

Второй закон Кирхгофа

В любом замкнутом контуре электрической цепи алгебраическая сумма ЭДС равна алгебраической сумме падений напряжений на всех его участках

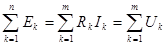(1.21)

где n – число источников ЭДС в контуре;

m – число элементов с сопротивлением R_k в контуре;

U_k=R_kI_k – напряжение или падение напряжения на k-м элементе контура.

Для схемы (рис. 1.2) запишем уравнение по второму закону Кирхгофа:

E=U_R+U₁.

Если в электрической цепи включены источники напряжений, то второй закон Кирхгофа формулируется в следующем виде: алгебраическая сумма напряжений на всех элементах контру, включая источники ЭДС равна нулю

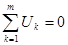(1.22)

При записи уравнений по второму закону Кирхгофа необходимо:

1) задать условные положительные направления ЭДС, токов и напряжений;

2) выбрать направление обхода контура, для которого записывается уравнение;

3) записать уравнение, пользуясь одной из формулировок второго закона Кирхгофа, причем слагаемые, входящие в уравнение, берут со знаком «плюс», если их условные положительные направления совпадают с обходом контура, и со знаком «минус», если они противоположны.

Запишем уравнения по II закону Кирхгофа для контуров электрической схемы (рис. 1.2):

контур I: E=RI+R₁I₁+r₀I,

контур II: R₁I₁+R₂I₂=0,

контур III: E=RI+R₂I₂+r₀I.

В действующей цепи электрическая энергия источника питания преобразуется в другие виды энергии. На участке цепи с сопротивлением R в течение времени t при токе I расходуется электрическая энергия

W=I²Rt. (1.23)

Скорость преобразования электрической энергии в другие виды представляет электрическую мощность

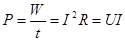. (1.24)

Из закона сохранения энергии следует, что мощность источников питания в любой момент времени равна сумме мощностей, расходуемой на всех участках цепи.

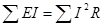. (1.25)

Это соотношение (1.25) называют уравнением баланса мощностей. При составлении уравнения баланса мощностей следует учесть, что если действительные направления ЭДС и тока источника совпадают, то источник ЭДС работает в режиме источника питания, и произведение EI подставляют в (1.25) со знаком плюс. Если не совпадают, то источник ЭДС работает в режиме потребителя электрической энергии, и произведение EI подставляют в (1.25) со знаком минус. Для цепи, показанной на рис. 1.2 уравнение баланса мощностей запишется в виде:

EI=I²(r₀+R)+I₁²R₁+I₂²R₂.

При расчете электрических цепей используются определенные единицы измерения. Электрический ток измеряется в амперах (А), напряжение – в вольтах (В), сопротивление – в омах (Ом), мощность – в ваттах (Вт), электрическая энергия – ватт-час (Вт-час) и проводимость – в сименсах (См)

Кроме основных единиц используют более мелкие и более крупные единицы измерения: миллиампер (1 мA = 10^–3 А), килоампер (1 кA = 10³ А), милливольт (1 мВ = 10^–3 В), киловольт (1 кВ = 10³ В), килоом (1 кОм = 10³ Ом), мегаом (1 МОм = 10⁶ Ом), киловатт (1 кВт = 10³ Вт), киловатт-час (1 кВт-час = 10³ ватт-час).

Баланс мощности

Прохождение электрического тока по проводнику сопровождается выделением тепла. Согласно закону Джоуля-Ленца, вся электрическая энергия, сообщаемая проводнику в результате работы сил электрического поля, превращается в тепловую энергию. С помощью закона Ома можно записать для потребителя с сопротивлением R:

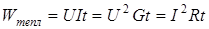(1.26)

Обычно под законом Джоуля-Ленца понимают уравнение, определяющее не энергию, а мощность тепловых потерь

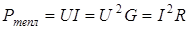(1.27)

В приведенных выражениях тепловая энергия и мощность выражаются в Джоулях [Дж]и Ваттах [Вт] соответственно.

Сформулированный закон распространяется на ветви, содержащие как пассивные, так и активные элементы. С этой целью пользуются обобщенным законом Ома (1.24)

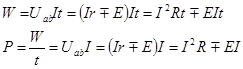(1.28)

Выражения (1.28), записанные для ветви с источником напряжения, справедливы и для ветви с источником тока, если произвести подстановку 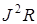вместо 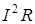и 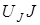вместо .

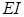Отсюда следует закон сохранения энергии, согласно которому алгебраическая сумма мощностей, подводимых ко всем ветвям разветвленной электрической цепи, равна нулю:

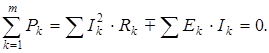(1.29)

Существует еще одна форма записи баланса мощности:

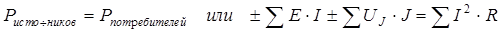. (1.30)

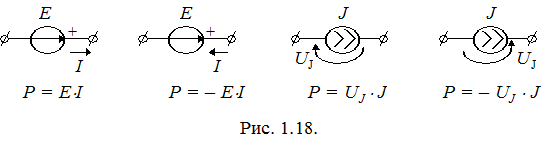
В левой части суммируются мощности источников энергии, а в правой – мощности, преобразованные в потребителях в тепло. Мощности источников, отдающих энергию, берутся со знаком «+», а работающих в режиме потребителей – со знаком «–» (рис. 1.18.).

Иногда пользуются уравнением баланса мощности в арифметической форме

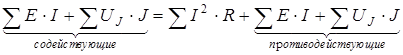. (1.31)

Здесь мощности противодействующих источников считаются положительными, но при балансе учитываются как мощности потребителей.