Задача 15. Решить смешанную задачу для данного неоднородного волнового уравнения с нулевыми начальными и граничными условиями
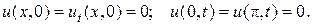
1. 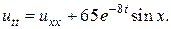 2.
2. 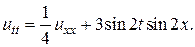
3. 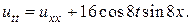 4.
4. 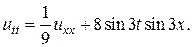
5. 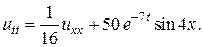 6.
6. 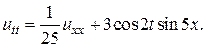
7. 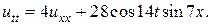 8.
8. 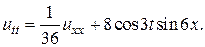
9. 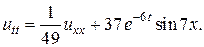 10.
10. 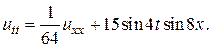
11. 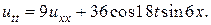 12.
12. 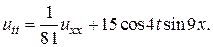
13. 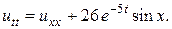 14.
14. 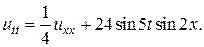
15. 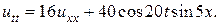 16.
16. 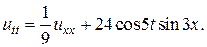
17. 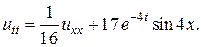 18.
18. 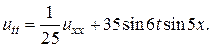
19. 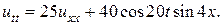 20.
20. 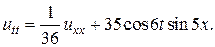
21. 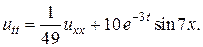 22.
22. 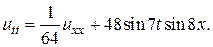
23. 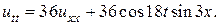 24.
24. 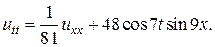
25. 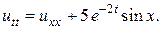 26.
26. 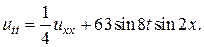
27. 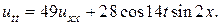 28.
28. 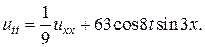
29. 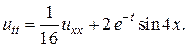 30.
30. 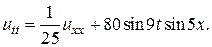
31. 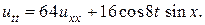
11.4. Справочный материал :
1) Задача Штурма-Лиувилля:
- дифференциальное уравнение 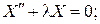
- граничные условия 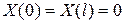 .
.
Разыскиваются значение параметра 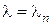 (собственные числа), при которых существуют ненулевые решения дифференциального уравнения, удовлетворяющие граничным условиям, а также и сами ненулевые решения (собственные функции).
(собственные числа), при которых существуют ненулевые решения дифференциального уравнения, удовлетворяющие граничным условиям, а также и сами ненулевые решения (собственные функции).
Рассматриваются и задачи Штурма-Лиувилля с граничными условиями вида
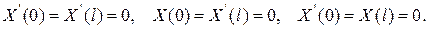
2) Смешанная задача для волнового уравнения на отрезке 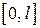 c однородными граничными условиями :
c однородными граничными условиями :
- дифференциальное уравнение 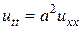 ;
;
- начальные условия 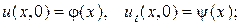
-граничные условия 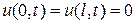 .
.
Рассматриваются также однородные граничные условия следующих видов :
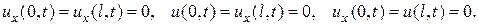
Решение этой задачи по методу Фурье получается в виде
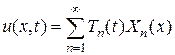
где 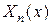 - собственные функции задача Штурма-Лиувилля с условиями, соответствующими рассматриваемым граничным условиям;
- собственные функции задача Штурма-Лиувилля с условиями, соответствующими рассматриваемым граничным условиям;
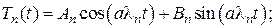
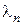 - собственные числа задачи Штурма-Лиувилля;
- собственные числа задачи Штурма-Лиувилля; 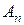 ,
, 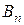 - коэффициенты, определяемые по начальным условиям.
- коэффициенты, определяемые по начальным условиям.
3) Смешанная задача для неоднородного волнового уравнения
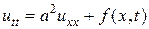
Ее решение можно получить в виде разложения по собственным функциям задачи Штурма-Лиувилля
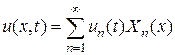
где 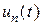 - решения задачи Коши
- решения задачи Коши

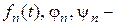 коэффициенты разложений
коэффициенты разложений
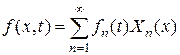 ,
, 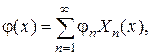
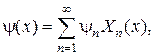
4) Смешанная задача для уравнения теплопроводности на отрезке 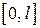 с однородными граничными условиями :
с однородными граничными условиями :
- дифференциальное уравнение 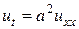 ;
;
- начальное условие 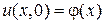
- граничные условия 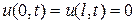
или одно из
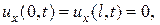
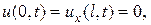
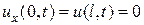
Решение этой задачи по методу Фурье получается в виде
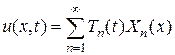 ,
,
где 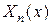 - собственные функции задачи Штурма – Лиувилля с условиями, соответствующими рассматриваемым граничным условиями;
- собственные функции задачи Штурма – Лиувилля с условиями, соответствующими рассматриваемым граничным условиями;
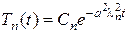
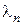 - собственные числа задачи Штурма-Лиувилля;
- собственные числа задачи Штурма-Лиувилля; 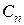 - коэффициенты, определяемые по начальным условиям.
- коэффициенты, определяемые по начальным условиям.
5) Смешанная задача для неоднородного уравнения теплопроводности
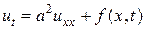 .
.
Ее решение можно получить в виде разложения по собственным функциям задачи Штурма-Лиувилля
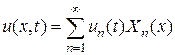
где 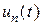 - решение задачи Коши
- решение задачи Коши
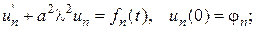
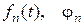 - коэффициенты разложений
- коэффициенты разложений
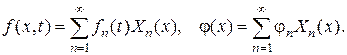
6) Смешанные задачи для волнового уравнения и уравнения теплопроводности с неоднородными граничными условиями
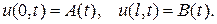
Каждая из этих задач сводится к задаче с однородными граничными условиями для функции
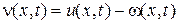
где
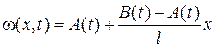
Решение получается в виде
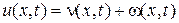
7) Краевая задача для уравнения Лапласа в круговом секторе
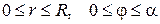
( 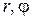 - полярные координаты,
- полярные координаты, 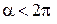 ):
):
- дифференциальное уравнение 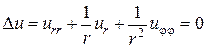 ,
,
-граничные условия
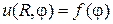 , (11.1)
, (11.1)
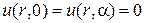 . (11.2)
. (11.2)
Вместо (11.2) рассматриваются и условия
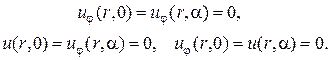 (11.3)
(11.3)
Решение задачи по методу Фурье получается в виде
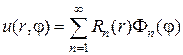
где 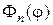 - собственные функции задачи Штурма-Лиувилля для дифференциального уравнения
- собственные функции задачи Штурма-Лиувилля для дифференциального уравнения
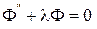
с условиями, соответствующими рассматриваемым граничным условиям вида (11.2) и (11.3);
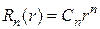
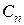 - коэффициенты, определяемые по граничным условиям (11.1).
- коэффициенты, определяемые по граничным условиям (11.1).
8) Задача Дирихле для уравнения Лапласа в круге
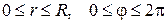
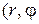 - полярные координаты):
- полярные координаты):
- дифференциальное уравнение 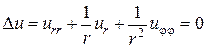 ;
;
- граничное условие 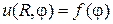 .
.
Решение этой задачи по методу Фурье получается в виде
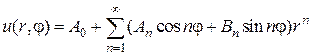
где 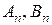 - коэффициенты, определяемые по граничным условиям.
- коэффициенты, определяемые по граничным условиям.
Приложения
Приложение 1
Таблица эквивалентных бесконечно малых функций
и асимптотических разложений (при 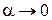 )
)
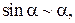 | 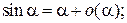 |
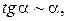 | 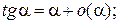 |
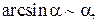 | 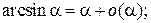 |
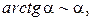 | 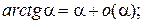 |
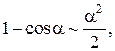 | 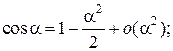 |
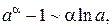 | 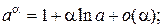 |
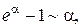 | 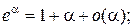 |
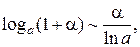 | 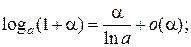 |
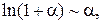 | 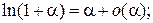 |
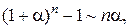 | 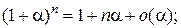 |
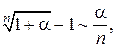 | 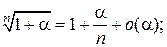 |
 | 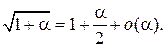 |
Приложение 2
Таблица производных
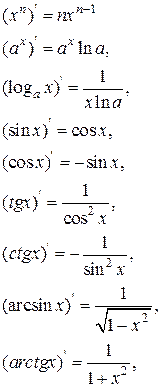 | 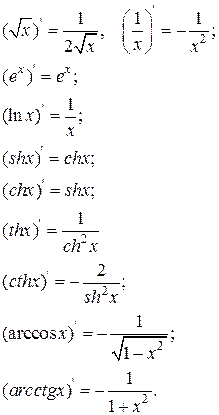 |
Приложение 3
Правила дифференцирования
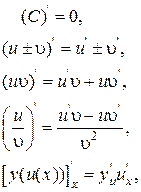 | 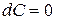 (С- постоянная); (С- постоянная); 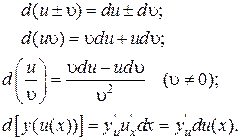 |
Приложение 4
Таблица интегралов
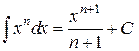 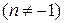 , , 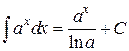 , , 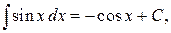 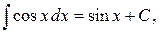 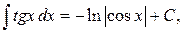 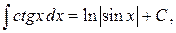 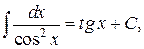 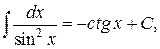 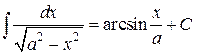 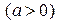 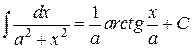 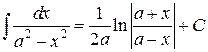 | 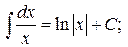 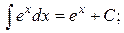 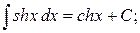 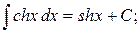 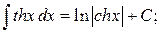 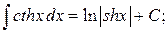 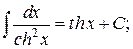 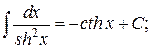 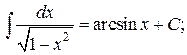 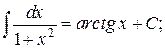 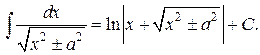 |
Приложение 5
