Уравнения математической физики

Введение

Уравнения математической физики.

Волновое уравнение.

Уравнение теплопроводности.

Уравнение Лапласа.

Метод конечных разностей (метод сеток).

Решение задач методом конечных разностей.

Решение задания методом конечных разностей.

3. Решение краевой задачи методом Фурье:

Метод Фурье для уравнений гиперболического типа

Решение задания методом Фурье для гиперболического типа

Сравнение методов решения

Сравнение результатов методом сеток и методом Фурье

Определить точность вычисления

Введение

Изучением дифференциальных уравнений в частных производных занимается математическая физика. Основы теории этих уравнений впервые были изложены в знаменитом "Интегральном исчислении" Л. Эйлера. Круг вопросов математической физики тесно связан с изучением различных физических процессов. Сюда относятся явления, изучаемые в гидродинамике, теории упругости, электродинамике и т.д. Возникающие при этом математические задачи содержат много общих элементов и составляют предмет математической физики. Постановка задач математической физики, будучи тесно связанной с изучением физических проблем, имеет свои специфические черты. Так, например, начальная и конечная стадии процесса носят качественно различный характер и требуют применения различных математических методов.

Уравнения математической физики

Дифференциальные уравнения с частными производными, а также некоторые родственные уравнения иных типов (интегральные, интегро-дифференциальные и т.д.), к которым приводит математический анализ физических явлений. Для теории У. м. ф. характерна постановка задач в таком виде, как это необходимо при исследовании физического явления. Круг У. м. ф. с расширением области применения математического анализа также неуклонно расширяется. При систематизации полученных результатов появляется необходимость включить в теорию У. м. ф. уравнения и задачи более общего вида, чем те, которые появляются при анализе конкретных явлений; однако и для таких уравнений и задач характерно то, что их свойства допускают более или менее наглядное физическое истолкование

Классификация уравнений математической физики

Линейное уравнение второго порядка, содержащее две независимые переменные, имеет вид

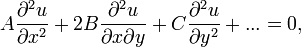
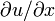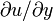где A, B, C — коэффициенты, зависящие от переменных x и y, а многоточие означает члены, зависящие от x, y, u и частных производных первого порядка: и . Это уравнение похоже на уравнение конического сечения:

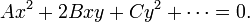
Так же, как конические сечения разделяются на эллипсы, параболы и гиперболы, в зависимости от знака дискриминанта D = B² − AC, классифицируются уравнения второго порядка в заданной точке:

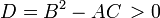1. — Гиперболическое уравнение,
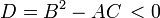2. — Эллиптическое уравнение,
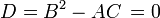3. — Параболическое уравнение (здесь предполагается, что в данной точке коэффициенты A, B, C не обращаются в нуль одновременно).

В случае, когда все коэффициенты A, B, C — постоянные, уравнение имеет один и тот же тип во всех точках плоскости переменных x и y. В случае, если коэффициенты A, B, C непрерывно зависят от x и y, множество точек, в которых данное уравнение относится к гиперболическому (эллиптическому), типу образует на плоскости открытую область, называемую гиперболической (эллиптической), а множество точек, в которых уравнение относится к параболическому типу, замкнуто. Уравнение называется смешанным (смешанного типа), если в некоторых точках плоскости оно гиперболическое, а в некоторых — эллиптическое. В этом случае параболические точки, как правило, образуют линию, называемую линией смены типа или линией вырождения.

Волновое уравнение

Волновое уравнение в математике — линейное гиперболическое дифференциальное уравнение в частных производных, задающее малые поперечные колебания тонкой мембраны или струны, а также другие колебательные процессы в сплошных средах (акустика, преимущественно линейная: звук в газах, жидкостях и твёрдых телах) и электромагнетизме (электродинамике). Находит применение и в других областях теоретической физики, например при описании гравитационных волн.

Уравнением колебания струны записывается в виде:

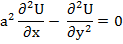
1.2 Уравнение теплопроводности:

Дифференциальное уравнение с частными производными параболического типа, описывающее процесс распространения теплоты в сплошной среде (газе, жидкости или твёрдом теле); основное уравнение математической теории теплопроводности . Т. у. выражает тепловой баланс для малого элемента объёма среды с учётом поступления теплоты от источников и тепловых потерь через поверхность элементарного объёма вследствие теплопроводности. Для изотропной неоднородной среды Т. у. имеет вид:

1.3 Уравнение Лапласа в двумерном случае:

Уравнение Лапласа — дифференциальное уравнение в частных производных. В двумерном пространстве уравнение записывается так:

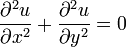
Уравнение Лапласа возникает во многих физических задачах механики, теплопроводности, электростатики, гидравлики. Несмотря на то, что уравнение Лапласа является одним из самых простых в математической физике, его решение сталкивается с трудностями. Особенно трудным бывает численное решение из-за нерегулярности функций и наличия особенностей.