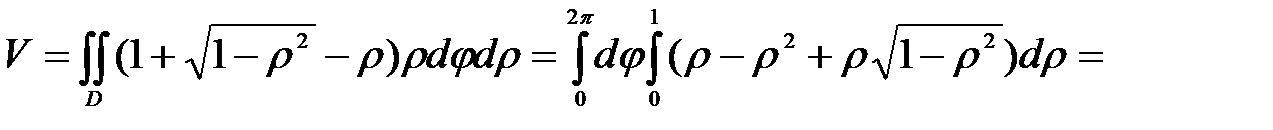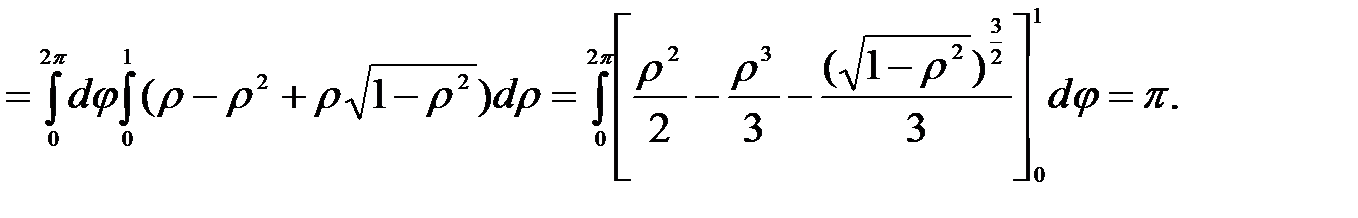Вычисление тройного интеграла

Пусть поверхность, ограничивающая область V снизу, имеет уравнение 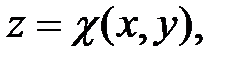а поверхность, ограничивающая эту область сверху, имеет уравнение 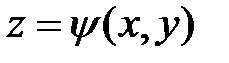(рис.27).

Введём понятие трёхкратного интеграла 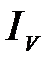, по области V от функции трёх переменных 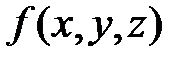, определённой и непрерывной в области V. Пусть область V проектируется на плоскость Оху в область D, которая ограничена линиями:

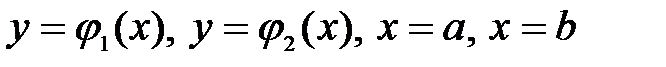
Тогда трёхкратный интеграл от функции 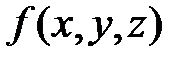по области V определя­ется так:

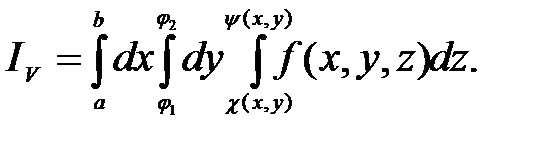
Сначала интегрируем внутренний интеграл по z, и после подстановки пределов интегрирования получаем функцию от х и у. Далее, вычисляется двойной интеграл от этой функции по области D.

Пример 21. Вычислить трёхкратный интеграл 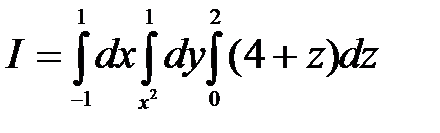и построить область интегрирования.

Решение. Последовательно вычислим три обыкновенных (однократных) определённых интеграла, начиная с внутреннего:

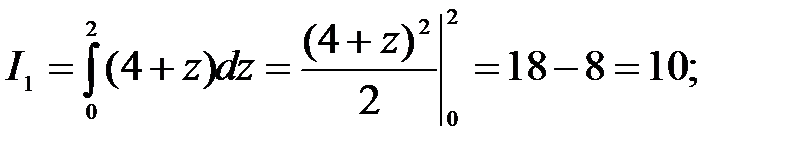
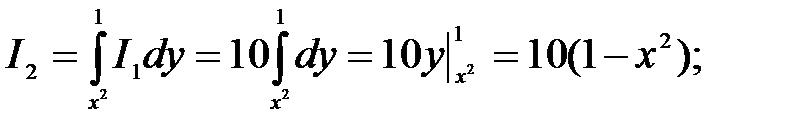
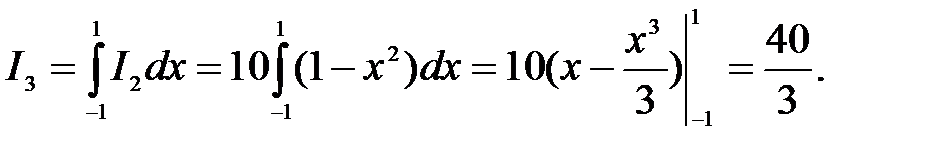
Для построения области интегрирования данного трёхкратного интеграла напишем уравнения поверхностей, ограничивающих эту область. Приравнивая переменную интегрирования каждого интеграла его пределам, получим сле­дующие уравнения:

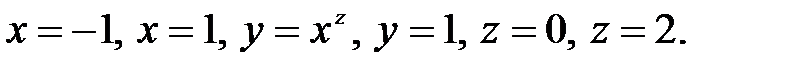
Это прямой цилиндр, образующие которого параллельны оси Oz (рис. 29).

Пример 20. Вычислить тройной интеграл 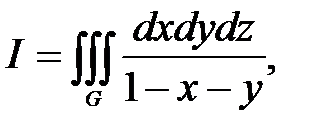если область G

ограничена плоскостями: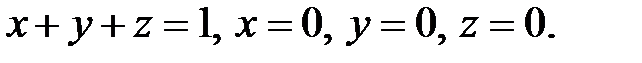

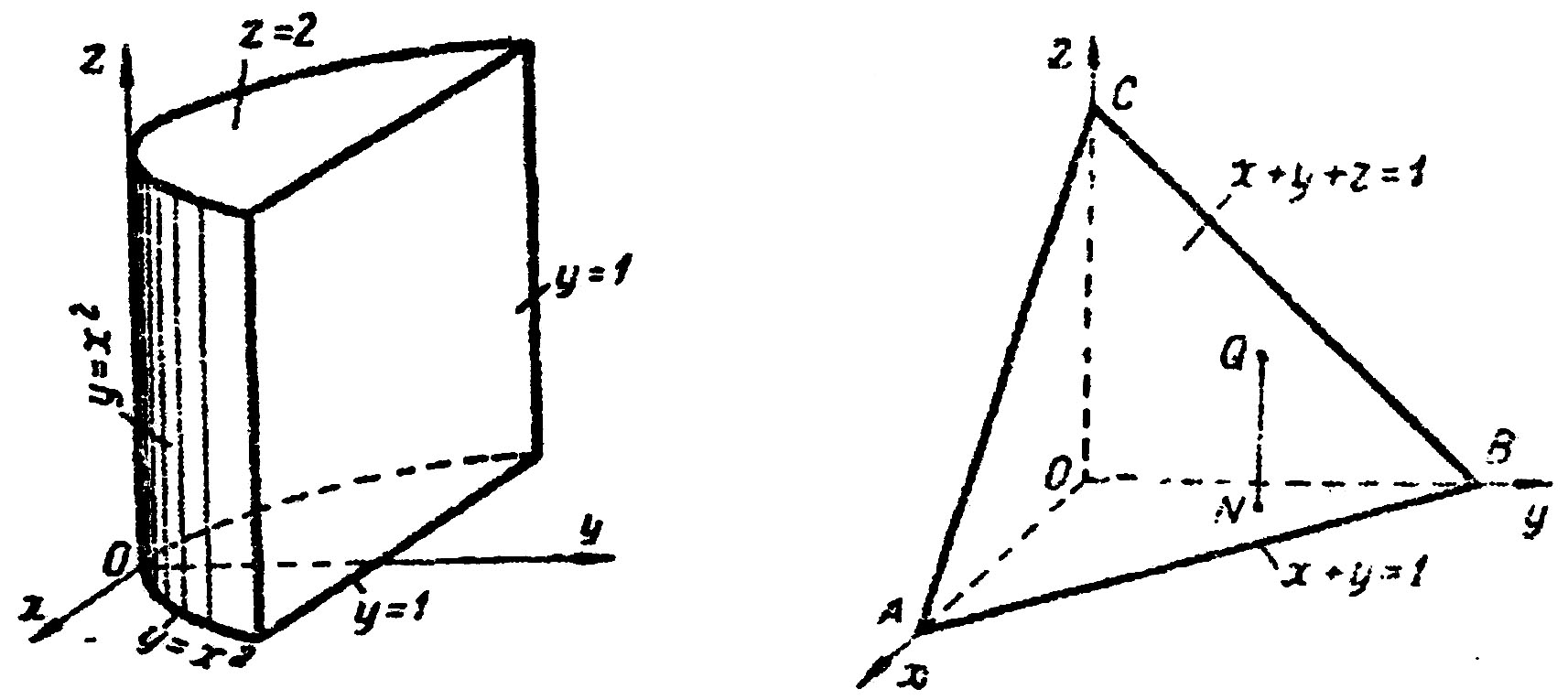
Рис. 29 Рис. 30

Решение. Построим данную область. Это есть тетраэдр (рис. 30). Прове­дём прямую параллельно оси 0z через эту область. Нижняя плоскость, которую пересекает прямая, будет плоскость АВО, уравнение которого 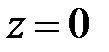. Верхняя граница, из которой выходит прямая, будет плоскость ABC, уравнение которо­го 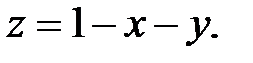Эти уравнения будут пределами внутреннего интеграла. Проек­цией всей области на плоскость Оху будет треугольник АВО. Следовательно,

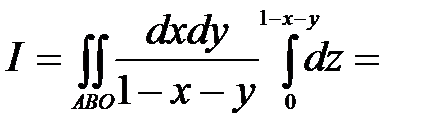
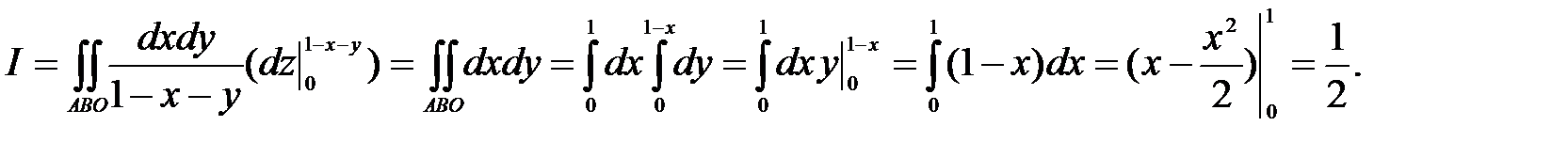
Пример 21. Вычислить тройной интеграл 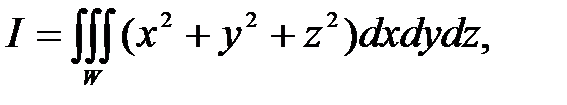где область W ограничена поверхностью .

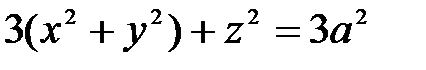Решение. Область W, ограниченная данной поверхностью, есть эллипсо­ид вращения (рис. 31). Его проекция на плоскость Оху есть круг 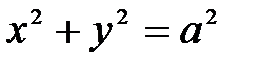.Т.о.

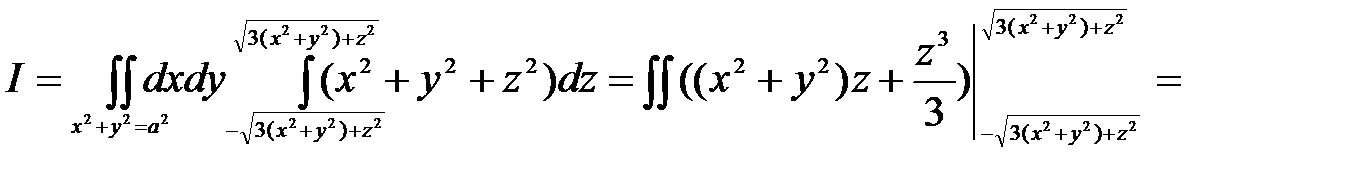
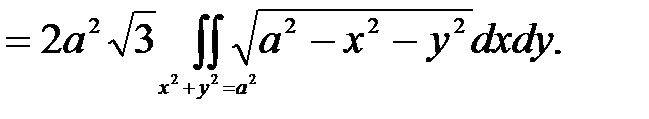
Перейдём в полярную систему координат. Полагая

.

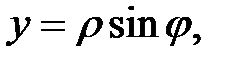
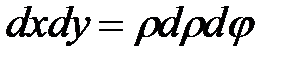Получим:

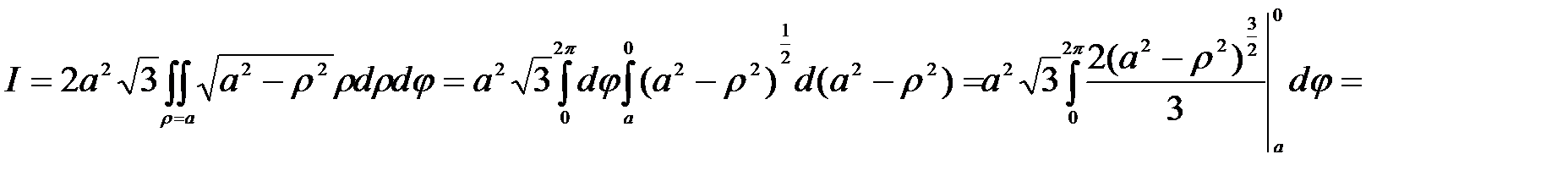
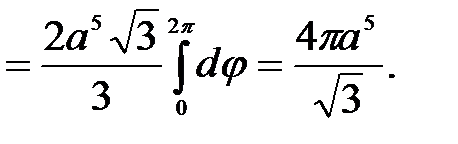
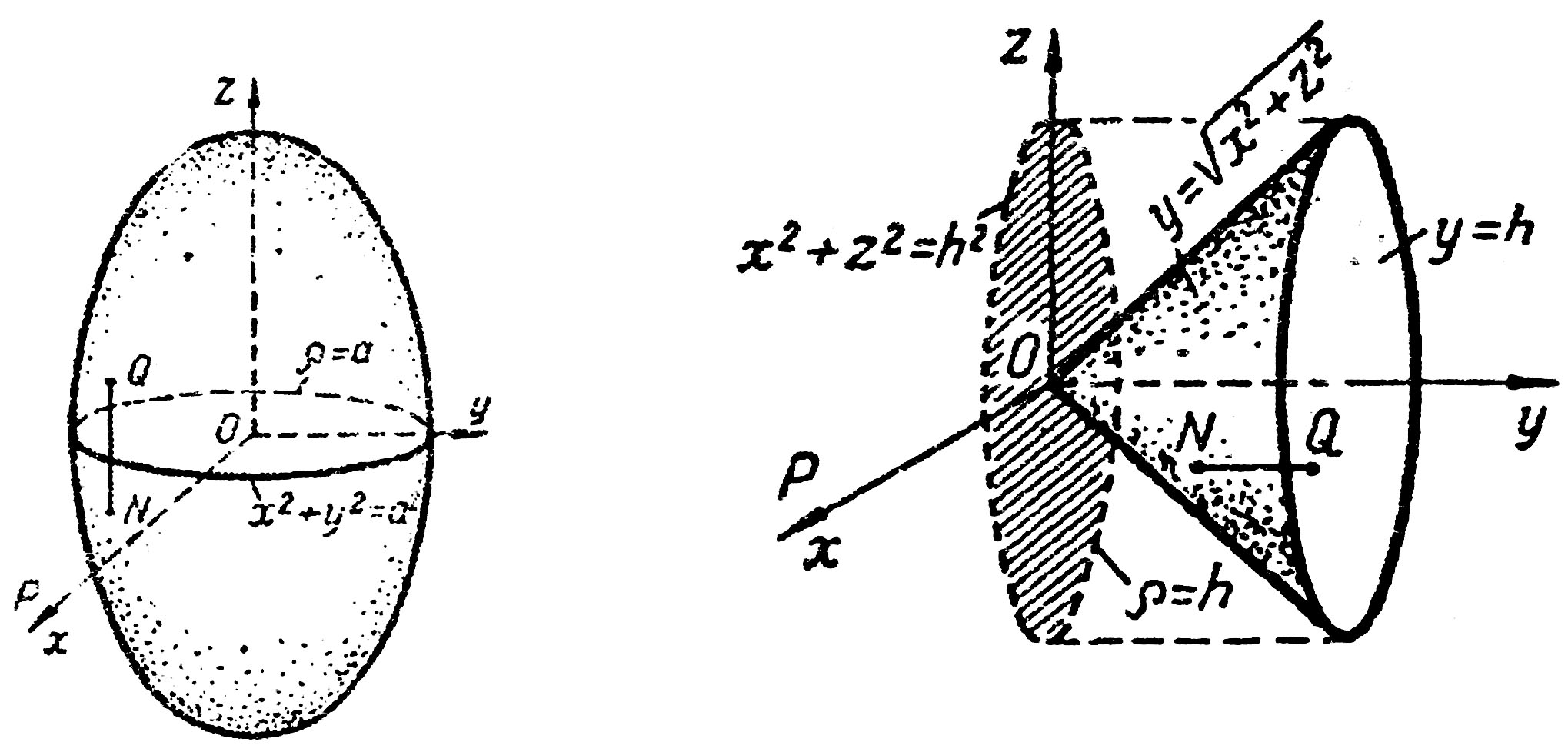
Рис. 31 Рис. 32

Пример 22. Вычислить тройной интеграл: 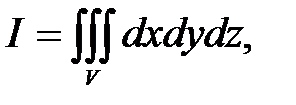где область V ограничена поверхностями .

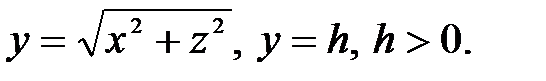Решение.Данная поверхностная область есть конус (рис. 32). Всякая прямая, проходящая через внутреннюю точку конуса параллельно оси Оу, пере­секает его границу в двух точках, а проекция этого конуса на плоскость Oxz есть круг 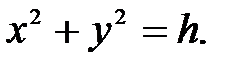. Меняя ролями z и у получим:

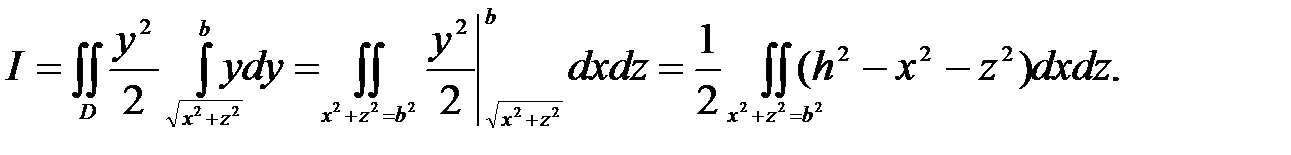
Переходя в полярную систему координат

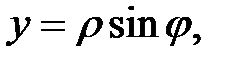
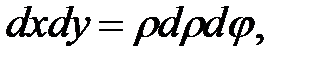
получим:

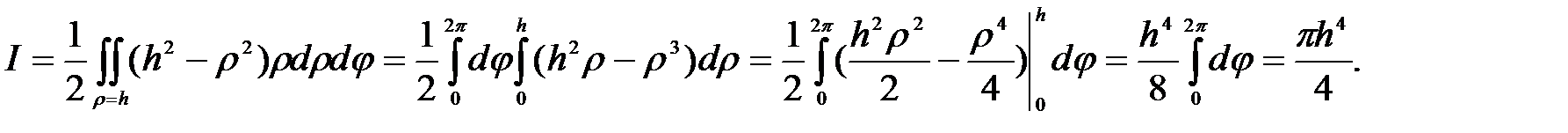
2.5. Вычисление объёма тела с помощью тройного интеграла

Если подынтегральная функция 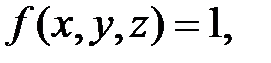то объём области V вычисляется с помощью тройного интеграла:

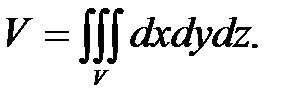
Пример 23. Вычислить объём тела, ограниченного сферической поверх­ностью 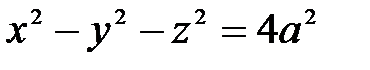и цилиндром 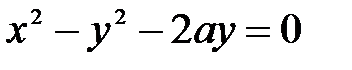и плоскостью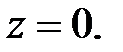

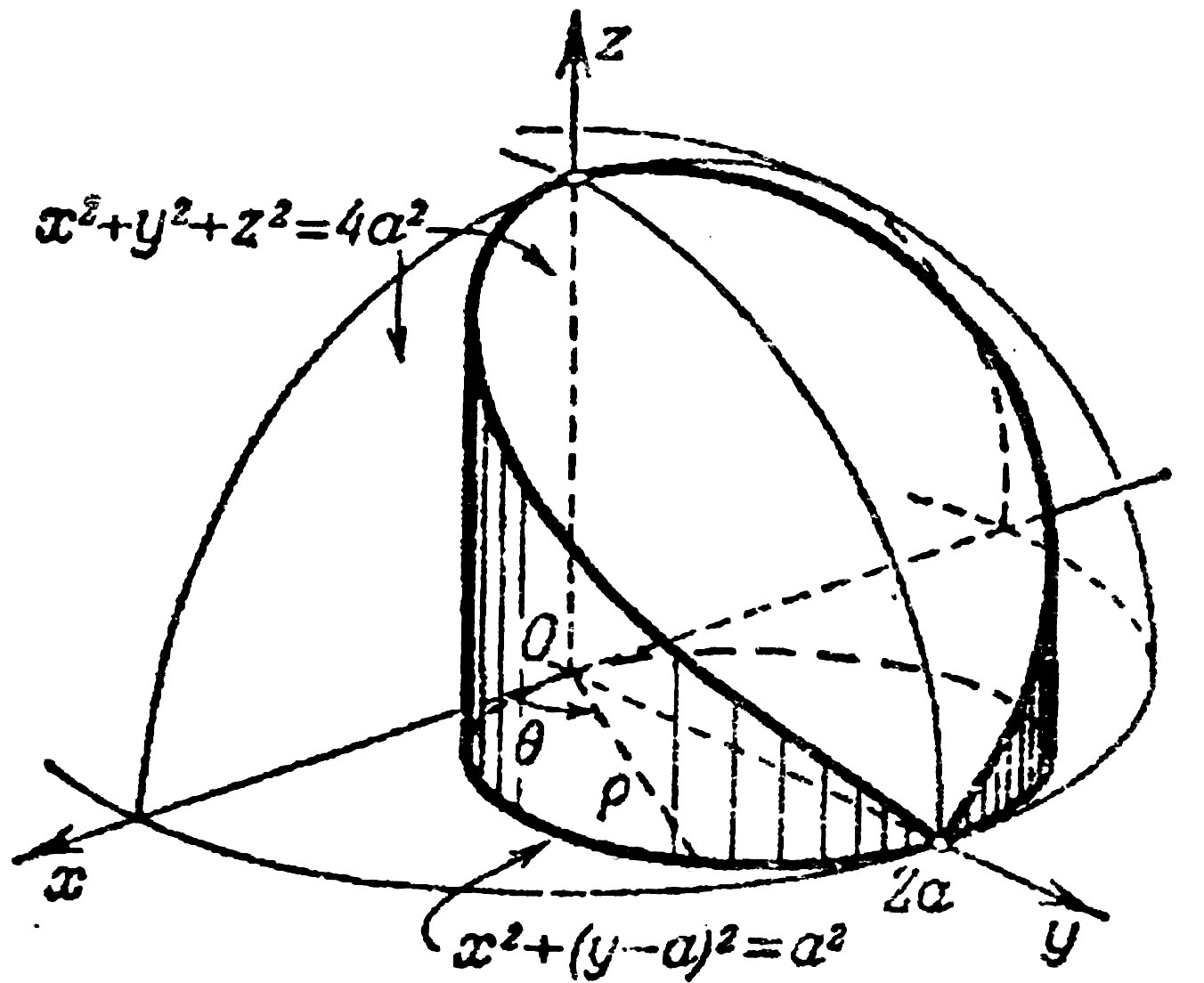
Рис.33

Решение.На рис. 33 представлена область, объём которой надо вычис­лить. Любая прямая, проведённая внутри этой области параллельно оси Oz, пе­ресечет снизу поверхность 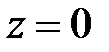, а сверху 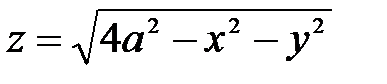этой области. Эти уравнения будут пределами интегрирования внутреннего интеграла. Проекцией всей области на плоскость Оху будет круг (рис. 33). Уравнение границы этого круга можно записать в виде 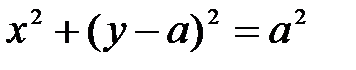. Вычислим 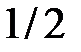искомого объёма V. Тогда в качестве области интегрирования двойного интеграла придётся взять полукруг, границы которого определяются уравнениями

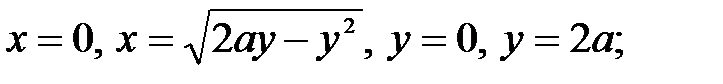
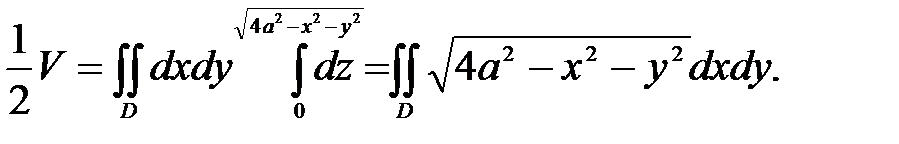
Перейдём в полярную систему координат .

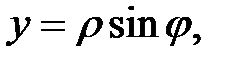
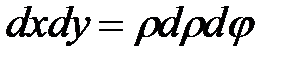Уравнение окружности примет вид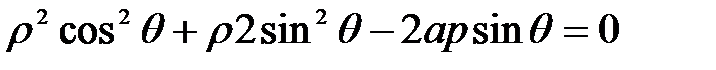

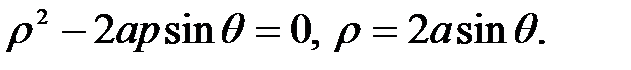
В полярной системе координат границы области определяются уравне­ниями 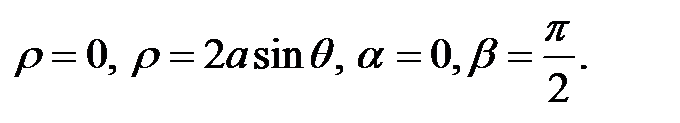Подынтегральная функция имеет вид

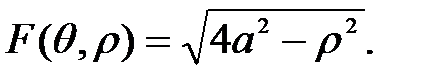
Получим

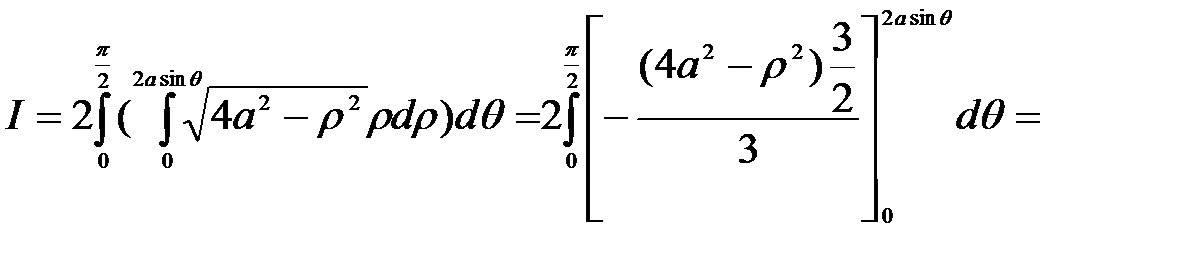
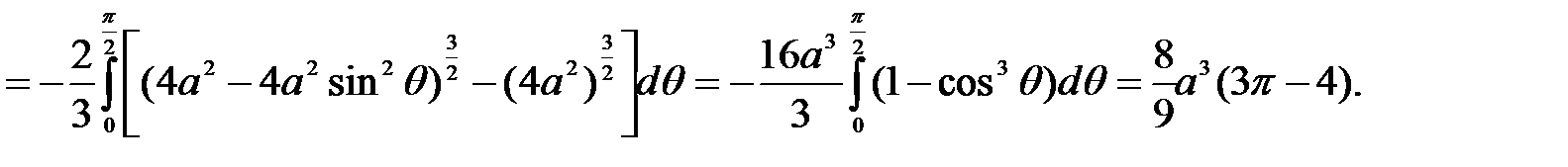
Пример 24. Найти объём тела, ограниченного данными поверхностями

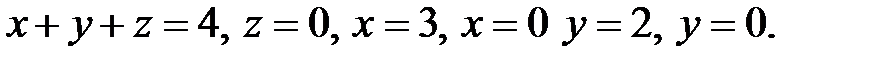
Решение. Данные плоскости ограничивают шестигранник (рис. 34).

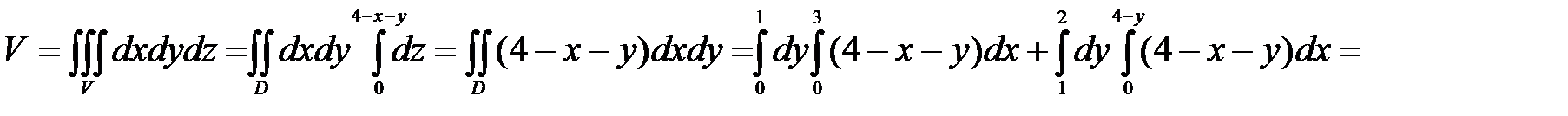
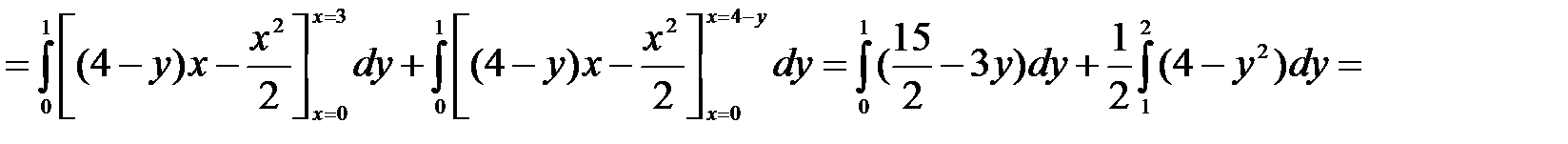
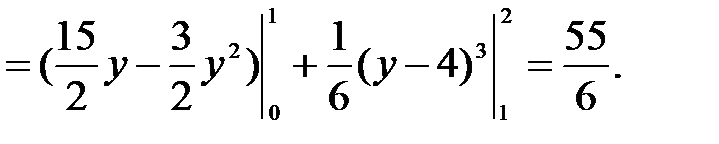
Здесь при вычислении двойного интеграла по области OABCD пришлось разбить её прямой BE параллельно оси ОХ, на две части.

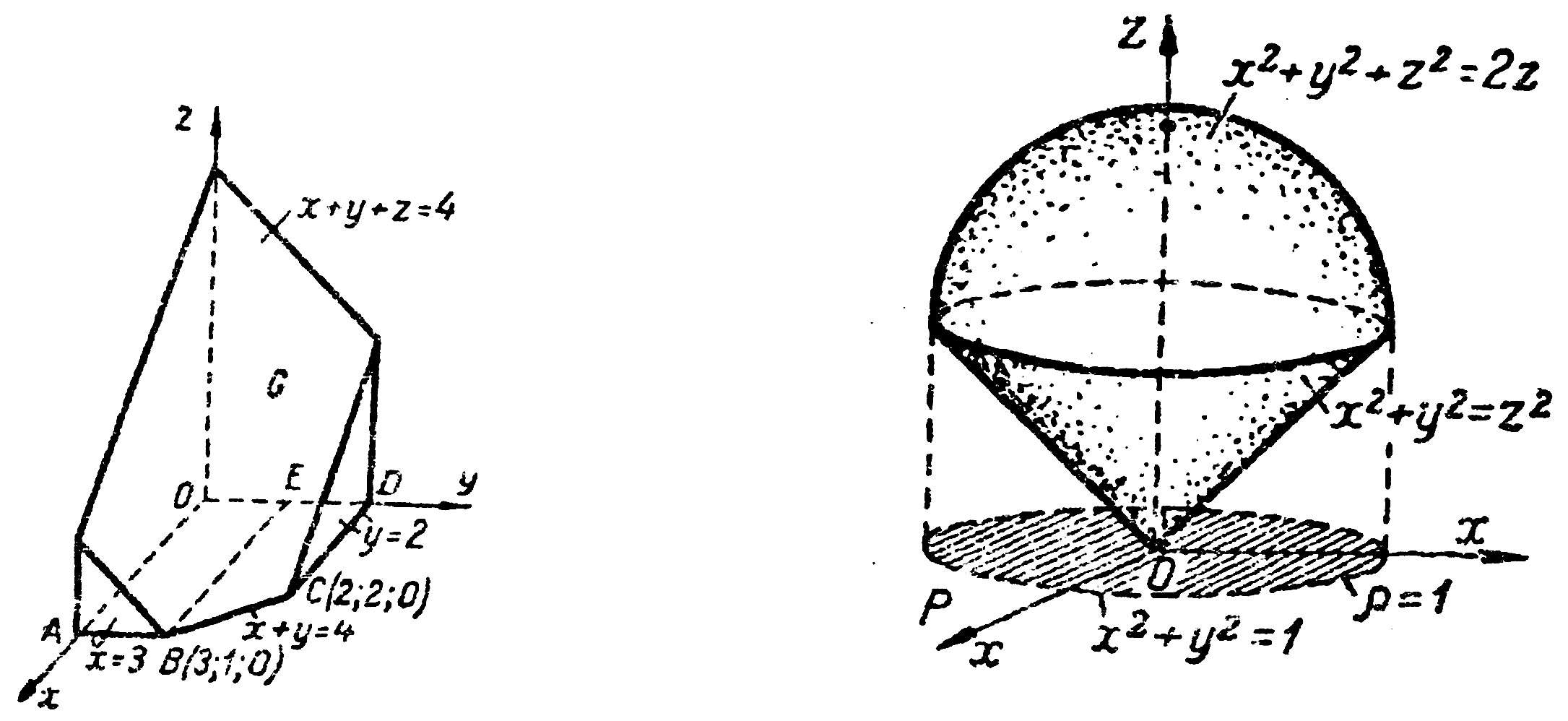
Рис. 34 Рис. 35

Пример 25.Найти объём тела, ограниченного данными поверхностями.

Решение. Тело, ограниченное сферой 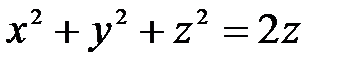(с центром в точке 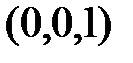) и конусом 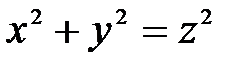, изображено на рис. 35. Любая прямая, проведён­ная внутри этой области параллельно оси 0z, пересечет снизу поверхность 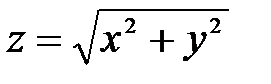, а сверху 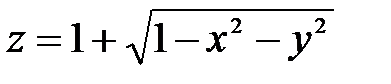этой области. Эти уравнения будут пре­делами интегрирования внутреннего интеграла. Проекцией всей области на плоскость Оху будет круг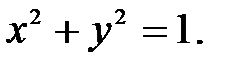

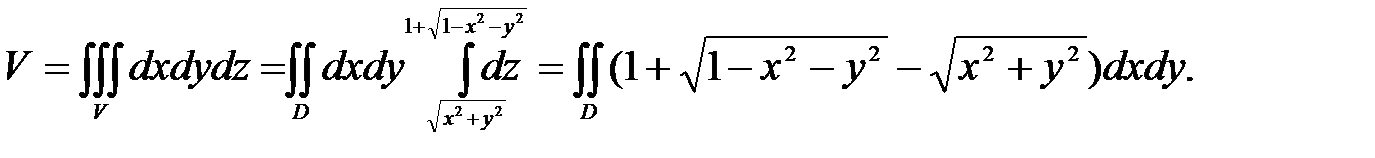
Переходя к полярным координатам, найдём: