Символічний метод розрахунку кіл синусоїдного струму

Дуже широке розповсюдження на практиці отримав символічний, або комплексний, метод розрахунку кіл синусоїдального струму.

Сутність символічного методу розрахунку полягає в тому, що при синусоїдальному струмі можна перейти від рівнянь, складених миттєвих значень і, які є диференційними рівняннями, до алгебраїчних рівнянь, складених відносно комплексів струму і е.р.с. Цей перехід оснований на тому, що в рівнянні, складеному за законом Кірхгофа для усталеного процесу, миттєве значення струму 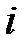замінюється комплексною амплітудою струму 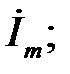миттєве значення напруги на активному опорі 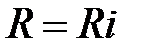– комплексом 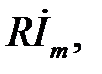по фазі співпадаючим зі струмом 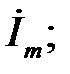миттєве значення напруги на індуктивності 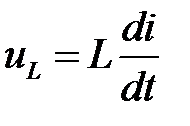– комплексом 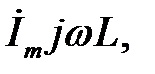що випереджає струм на 90°; миттєве значення напруги на ємності 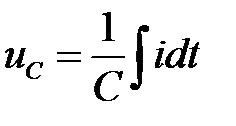– комплексом 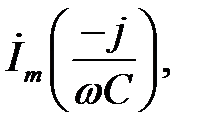що відстає від струму на 90°; миттєве значення е.р.с. – комплексом

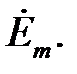
Амплітуда напруги на індуктивності рівна добутку амплітуди струму на 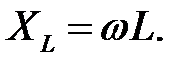Множник вказує на те, що вектор напруги на індуктивності випереджає вектор струму на 90°.

Аналогічно, що амплітуда напруги на ємності рівна амплітуді струму, помноженій на 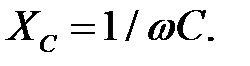Відставання напруги на ємності від струму, що по ній протікає, на 90° пояснюється наявністю множника .

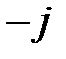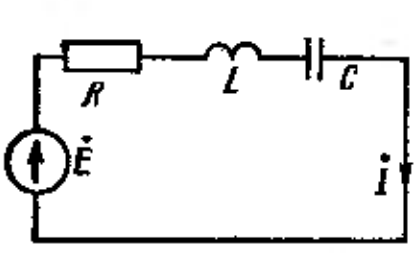
Рис. 31.1

Наприклад, для схеми рис. 31.1 рівняння для миттєвих значень можна записати так:

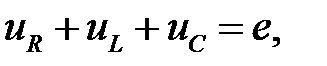або

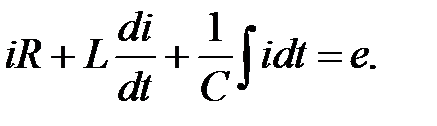(31.1)

Запишемо його в комплексній формі:

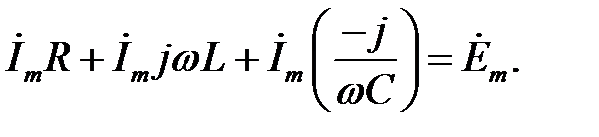Винесемо 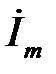за дужку:

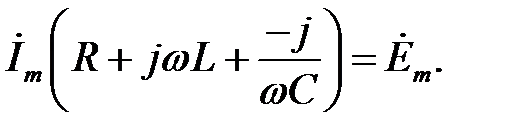(31.2)

Відповідно, для схеми рис. 31.1

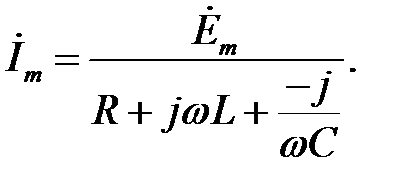(31.3)

Це рівняння дозволяє знайти комплексну амплітуду струму 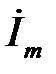через комплексну амплітуду е.р.с. 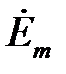і опір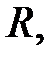 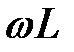і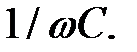

Метод називають символічним тому, що струм і напруга замінюються їх комплексним зображенням чи символами. Так, 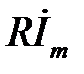– це зображення або символ спаду напруги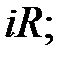 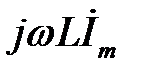– це зображення або символ спаду напруги на індуктивності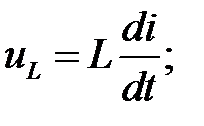 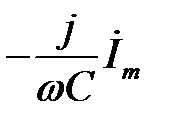– це зображення або символ спаду напруги на кондесаторі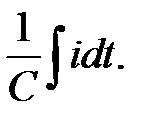

Комплексний опір.

Добуток 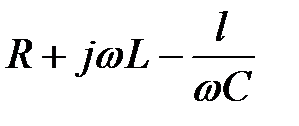в рівнянні 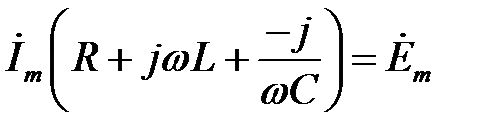являє собою комплекс, має розмірність опору і позначається через 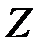. Його називають комплексним опором:

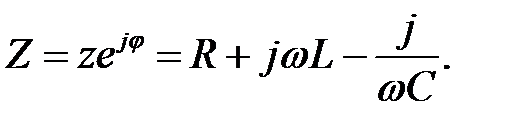(32.1)

Як і всякий комплекс 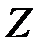можна записати в показниковій формі. Модуль комплексного опору прийнято позначати через 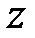. Точку над 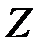не ставлять, тому що прийнято ставити її тільки над такими комплексними величинами, які відображають синусоїдальні функції часу.

Закон Ома для кола синусоїдного струму.

Рівняння 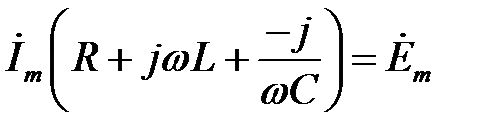можна записати так: 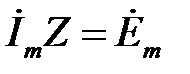. Розділимо обидві частини на 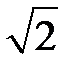і перейдемо від комплексних амплітуд 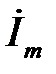і 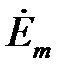до комплексних діючих значень 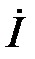і :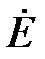

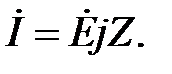(33.1)

Рівняння 33.1 являє собою закон Ома для кола синусоїдального струму.

В загальному випадку 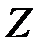має деяку дійсну частину і деяку уявну частину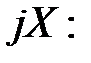

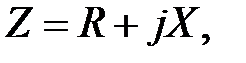(33.2)

де 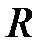– активний опір; 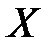– реактивний опір;

Рис. 31.1

Для схеми рис.33.1 реактивний опір

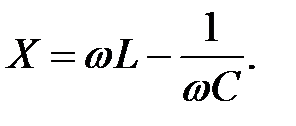(33.3)

КОРЖАК Ю.В

Комплексна провідність.

Під комплексною провідністю Y розуміють величину, зворотну комплексному опору Z:

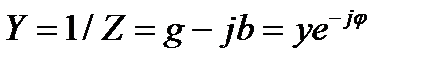
Вимірюють комплексну провідність в Ом^-1 або сименсах (См). дійсну частину її позначають через g, уявну через b. Оскільки

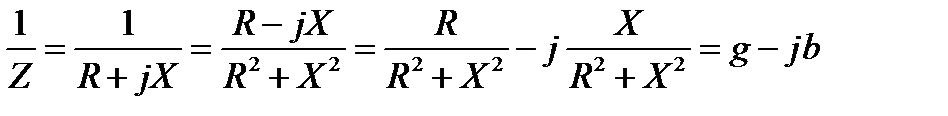
То

.

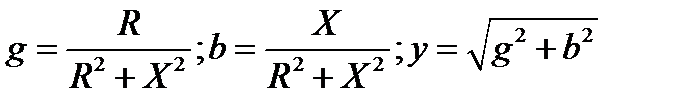Якщо Х позитивно, то і b позитивно, при Х негативному b також негативно.

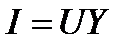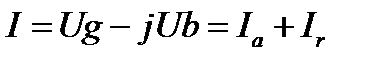При використанні комплексної провідності закон Ома записують так: или где 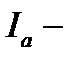активна складова струму; 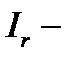реактивная складова струму; 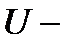напруга на ділянці ланцюга, опір короткого рівна Z.