Элементтерінің өзінің алгебралық толықтауышына, көбейтіндісінің қосындысына

А А А А А А А А А

Анықтауыштың бас диагоналының элементтері: a_11,a_n1…a_nn элемент.жиынтығын айтады

Анықтауыштың мәні қай жағдайда өзгермейді, жол. Барлық элемнт.сәйкес баған элемент.ауыстырса.

Анықтауыштың екі жолының сәйкес элементтері пропорционал болса, онда оның мәні неге тең?

Анықтауыштың кез келген жолының немесе бағанының элементтерін бір k санына көбейткеннен: оның мәні к есе аратды

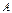матрицасын 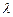санына көбейту: А матриц.әрбір элемен. λ сан.көбейткенмен мәндес

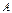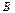және матрицаларын қай кезде көбейтуге болады. 1-ші матри. баған саны 2-ші мат.жол санына тең болса

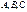үш матрицаны көбейту үшін қай теңдік орынды: (AB)C=A(BC)

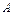матрицасының рангысының анықтамасы: осы матри. 0-ге тең емес минорлар. Ең үлкен ретін айт.

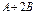матрицасын есептеңіз, мұндағы ,

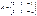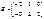
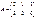, және 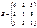матрицаларының қосындысын табыңыз: қосу мүмкін емес

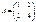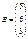және матрицаларының 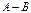айырымын табыңыз азайту мүмкін емес

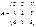матрицасын 2-ге көбейтіңіз: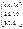

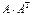көбейтіндісін есептеңіз, мұндағы ,

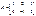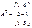
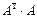көбейтіндісін есептеңіз, мұндағы , :

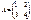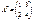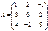матрицасын бірлік матрицаға көбейтіңіз: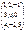

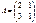және 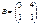берілгендері бойынша 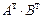көбейтіндісін табыңыз: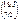

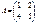матрицасына кері матрицаны табыңыз: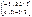

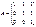матрицасына кері матрицаны табыңыз: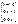

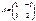матрицасына кері матрицаны табыңыз:A^-1=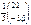

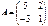матрицасына кері матрицаны табыңыз: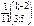

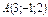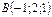және нүктелері берілген. 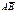векторының координаталарын табыңыз (-4;3;-1)

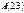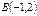және нүктелері берілген. 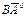бірлік векторының координаталарын көрсетіңіз (3\√10*1\√10)

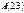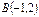және нүктелері берілген. 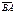векторының координаталарын табыңыз (3,1)

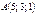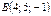және нүктелері берілген. 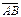векторының ұзындығын табыңыз 3

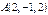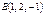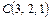, және нүктелері берілген. 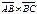векторлық көбейтіндісінің координаталарын табыңыз (6;-4;-6)

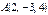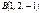, және 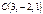төбелерінің координаталары бойыншаүшбұрыштыңауданын табыңыз5√2

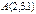нүктесінен өтетін және 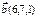векторына перпендикуляр болатын жазықтықтың теңдеуін жазыңыз 6(x-2)+7(y-3)+(z-1)=0

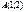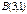және нүктелері арқылы өтетін түзудің теңдеуін жазыңыз 2y+x-5=0

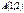нүктесінен 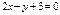түзуіне дейінгі арақашықтықты табыңыз 3\√5

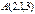нүктесі арқылы 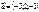векторына перпендикуляр өтетін жазықтықтың теңдеуін жазыңыз 3x-2y+z-7=0

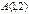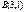және нүктелері арқылы өтетін түзудің теңдеуін жазыңыз 2y+x-5=0

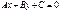теңдеуінде 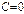болса, онда түзу қалай орналасқан? Координат.бас нүктесі арқы.өтед.

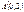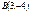және нүктелерінің ара қашықтығын табыңыз 3√5

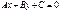түзуінде 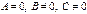болса, онда түзу...O_x осьіне паралель

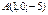нүктесі арқылы, 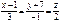түзуіне перпендикуляр өтетін жазықтықтың теңдеуін жазыңыз 3x-y+2z+7=0

Б Б Б Б Б Б Б Б Б Б Б

Бір ғана жолдан тұратын матрица қалай аталады:жол матр\а не\се жол векторы

Бір түзуде немесе параллель түзулердің бойында жатқан векторлар қалай аталады?коллинияр

Бір жазықтықта жатқан векторлар қалай аталады?компланар

Берілгені: 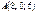, , 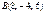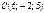. Табу керек: 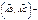? 8

Берілгені: 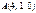, , 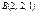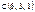. Табу керек: 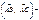?-1

Бұрыштық коэффициенті 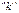-ға тең, 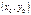нүктесі арқылы өтетін түзудің теңдеуі келесі түрде жазылады у-y₀=k(x-x₀)

Бұрыштық коэффициентпен берілген түзудің теңдеуін көрсет у=kx+b (y=kx+1)

Берілген 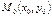нүктеден берілген 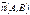векторға перпендикуляр өтетін түзудің теңдеуін көрсет A(x-x₀)+B(y-y₀)=0

Берілген 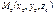нүкте арқылы, берілген 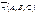векторға перпендикуляр өтетін жазықтықтың теңдеуін көрсет A(x-x₀)+B(y-y₀)+C(z-z₀)=0

Бағыттаушы векторы 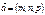болған, 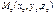нүктесі арқылы өтетін түзудің теңдеуін көрсет (x-x₀)/m=(y-y₀)/n=(z-z₀)/p

Берілген 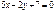түзуіне параллель болатын түзудің бұрыштық коэффициентін табыңыз 5/2

Бірінші тамаша шекті көрсетіңіз: lim_x-0sinx/x=1

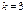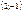Бұрыштық коэффициенті және нүктесі арқылы өтетін түзудің теңдеуін жазыңыз x-3x+7=0

Біртекті 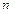белгісізді 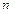сызықты теңдеулер жүйесінің бір ғана шешімі бар: x=0, егер x_A≠0

В В В В В В В В В В

Векторды скаляр көбейткенде мына теңдік орындалады aa=|a|²

ГГ Г Г Г Г Г Г Г Г Г Г

Гиперболаның канондық теңдеуін көрсет x²\a²-y²\b²=1

Д Д Д Д Д Д Д Д Д Д

Диагональ матрицаның анықтауышының мәні неге тең?

элементтерінің өзінің алгебралық толықтауышына, көбейтіндісінің қосындысына

Диагональ матрицаның мәні неге тең бас диагналь элемнт.көбейтіндісіне тең

Е Е Е Е Е Е Е Е Е Е Е

Егер анықтауышта кейбір жолдың немесе бағанның элементтерінің ортақ көбейткіші болса, онда: оны анық. таңба.алдына шығар.

Егер бір матрица екінші бір матрицадан элементар (жәй) түрлендіру арқылы алынса, онда ол матрицалар: эквивалентті д.а.

Есептеңіз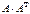

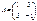
Егер 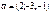векторының ұшы 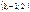нүктесінде болса, онда осы вектордың басының координаталары неге тең? (-1,2,3)

Егер 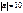, , 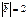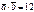болса, онда 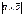неге тең?16

Егер 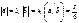болса, онда 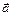және 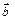векторларына тұрғызылған параллелограммның ауданы 6

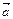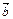Егер және векторлары коллиенар болса, онда бір ғана 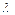саны табылып мына теңдікті қанағаттандырады b=λa

Егер 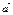, , 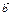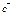комплонар емес векторлар болса онда, 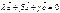теңдігі келесі жағдайда ғана орындалады α=β=γ=0

Егер 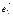, , 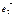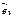векторлары кеңістіктегі базис болса, онда кез келген 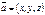векторын бір ғана жолмен былай жіктеп жазуға болады a=xe₁+ye₂+ze₃

Егер 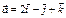, 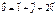болса, онда 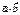тап 3

Егер 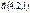, 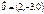векторлары берілсе, онда 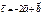векторының координатасын табыңыз c=(-6.-7.-2)

Егер 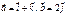болса, онда 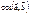неге тең? 0

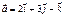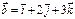Егер және векторлары берілсе, онда 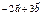неге тең? -i+11k

Егер 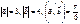болса, онда 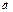және 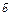векторларына салынған параллелограмныңауданы неге тең?6

Егер 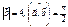болса, 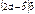неге тең 16

Егер 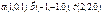болса, 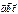-ны табыңыз 0

Егер 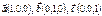болса, 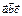табыңыз 1

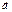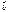Егер және векторлары ортогонал және 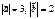болса, онда 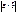табыңыз 6

Егер 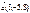, 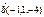болса, онда 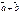векторын табыңыз 2,-4,4

Егер 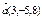, 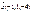берілсе, онда 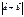-ны табыңыз 6

Егер 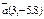, 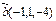берілсе, онда 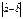-ны табыңыз 14

Егер 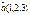, 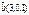болса, онда 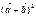-ны табыңыз 36

Егер 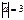, , 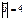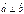болса, онда 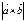-ны табыңыз 12

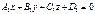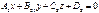Екі және жазықтықтарының арасындағы бұрыш келесі формуламен есептелінеді: cosα=A₁A₂+B₁B₂+C₁C₂/(A₁²+B₁²+C₁²)(A₂²+B₂²+C₂²)

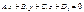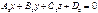Екі және жазықтықтарының параллельдік белгісін көрсет A_1/ A₂₌ B₁/ B₂=C₁/C₂

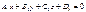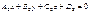Екі және жазықтықтарының перпендикулярлық белгісін көрсет A₁ A₂+ B₁ B₂+ C₁C₂=0

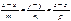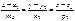Екі және түзу. арасындағы бұрышты қайсы формуламен есептейді cosα=m₁m₂+n₁n₂+p₁p₂/(m₁²+n₁²+p₁²)(m₂²+n₂²+p₁²)

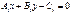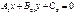Екі және түзу.арасы. бұрыш келесі форм. есептелінеді: cosa=A₁A₂+B₁B₂\√A²₁+B²₁√A²₂+B²₂

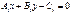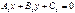Екі және түзу. параллельдік белгісін көрсет A_1/ A₂₌ B₁/ B₂

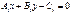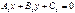Екі және түзу. перпендикулярлық белгісін көрсет A₁ A₂+ B₁B₂ =0

Екінші тамаша шекті көрсетіңіз: lim_x-∞(1+x)^1/x=e

Екінші тамаша шекті көрсетіңіз: lim_x-∞(1+1\x)^x=e

Егер 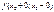шектері бар, бірақ 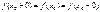теңдіктерінің ең болмағанда біреуі орындалмаса, онда 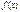функциясы 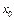нүктесінде үзіледі

Егер екi рет дифференциалданатын 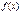функциясының 1-шi ретті туындысы 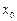нүктесiнде 0-ге тең, ал екiншi туындысы 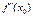осы нүктеде оң болса, онда ол қандай нүкте болады? X₀ min нүктесі

Егер екi рет дифференциалданатын 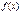функциясының 1-шi ретті туындысы 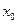нүктесiнде 0-ге тең, ал 2-шi туындысы 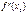осы нүктеде терiс болса, онда онда ол қандай нүкте болады? X₀ max нүктесі

Екi рет дифференциалданатын 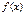функциясының 2-шi ретті туындысының иiлу нүктесiндегi мәнi неге тең? 0

Екi рет дифференциалданатын 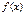функциясының 2-шi ретті туындысы 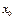нүктесiнің маңайында таңбасын өзгеретiн болса, онда 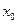- қандай нүкте болады? функ.иілу нүктесі.

Егер 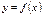функциясы 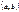интервалында өспелі болса, онда бірінші туындысы қандай болады? f^,(x)>0

Егер 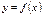функциясы 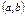интервалында кемімелі болса, онда бірінші туындысы қандай болады?f^,(x)<0

Егер 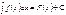болса, онда 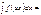1\aF(ax)+C

Егер 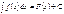болса, онда 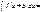F(x+b)+C

Егер 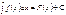болса, онда 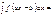1\aF(ax+b)+C

Егер 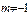болса, онда 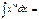x^m+1\m+1

Егер 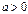, 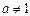болса, онда 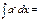a^x\lna+C

Егер 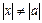болса, онда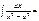

Егер 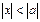болса, онда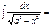

Егер 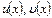- дифференциалданатын функциялар болса, онда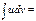

Егер 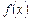функциясы 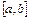кесіндісінде интегралданса және 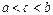теңсіздігі орындалса, онда

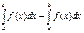
Егер 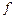, 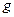функциялары 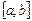кесіндісінде интегралданса және 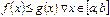, онда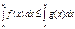

Егер 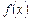функциясы 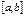кесіндісінде үзіліссіз болса және 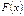оның қайсыбір алғашқы функциясы болса, онда 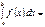F(b)-F(a)

Егер 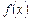функциясы жұп болса, онда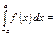

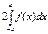
Егер 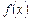функциясы тақ болса, онда 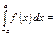0

Егер 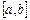кесіндісінде параметрлік теңдеумен берілген 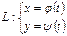қисығында 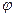, 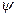функциялары үзіліссіз болса, онда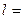

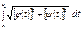
Егер 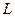қисығы 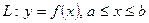теңдеуімен берілсе, онда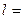

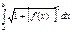
Егер 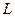қисығы поляр координат жүйесінде 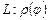, 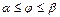теңдеуімен берілсе, онда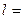

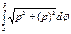
Егер 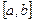кесіндісінде 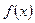функциясының таңбалары шектеулі рет ауысса, онда 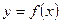, , 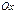, 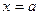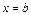сызықтарымен қоршалған 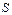жазық фигурасының ауданы былай есептелінеді: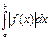

Егер x=1 болса, онда f(x)=(х²+1)\(х+1) функц.бірінші ретті туындысы мәнін таб.0,5

Ж Ж Ж Ж Ж Ж Ж Ж Ж Ж

Жазықтықтың жалпы теңдеуін көрсет Ax+By+Cz+D=0

Жазықтықтың кесінділік теңдеуін көрсет x\a+y\b+z\c=1

Жарты өстері 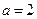, 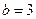болған және төбесі Ох өсіне орналасқан гиперболаның теңдеуін жазыңыз x²\4-y²\9=1

К К К К К К К К К К

Кері матрица мына формуламен табылады: A^-11\∆(A)*Ã^t

Қ Қ Қ Қ Қ Қ Қ Қ Қ Қ Қ

Қандай матрицалар тең матрицалар деп аталады?

Қандай матрица квадрат матрица деп аталады? жол саны баған санына тең болса

Қай шарт орындалса, матрицалар алмастырылымды деп аталады:AB=BA

Қандай матрицаның кері матрицасы болады? |A|≠0 болса

Қисық 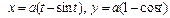теңдеуімен берілген. 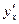-ті табыңыз: ctg t\2

Қисық 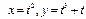теңдеуімен берілген. 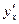-ті табыңыз: 3t²+1\2t….

Қисық 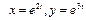теңдеуімен берілген. 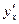-ті табыңыз: 3\2e^…

Қисық 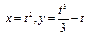теңдеуімен берілген. 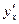-ті табыңыз: t²-1\2t

Л Л Л Л Л Л Л Л Л Л

Лопиталь ережесін пайдаланып шекті есептеңіз: 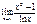2

Лопиталь ережесі бойынша шегін тап :∞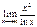

Лопиталь ережесі бойынша шегін тап 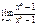2

М М М М М М М М М М

Матрицаның анықтамасы:

Матрицаларды қосу және азайту амалдары: өлшемдері бірдей матри.үшін орынд.

Матрицаның рангысы өзгермейді, егер: кез-келген екі жол н/е екі бағанын ауыстыр.

Материалдық нүктеге 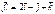, , 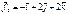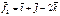күштері әсер етеді. Осы күштердің қортынды күші 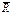-дің 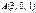нүктесінен 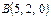нүктесіне орын ауыстырған кездегі атқарған жұмысын табыңыз 7

Материалдық нүктені 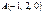нүктесінен 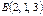нүктесіне 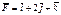күші жылжытады.Осы күштің жұмысын есептеңіз4

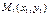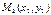және нүктелері арқылы өтетін түзудің теңдеуін көрсет y-y₁\y₂-y₁=x-x₁\x₂-x₁

M(x₁,y₁)және M(x₂,y₂) нүктелерінің ара қашықтығын өлшей.формула d=√(x₂-x₁)²+(y₂-y₁)²

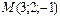нүктесінен 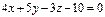жазықтығына дейінгі арақашықтықты табыңыз3\√2

Мына 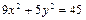теңдеу жазықтықта қандай қисықты анықтайды? эллипс

Мына 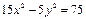теңдеу жазықтықта қандай қисықты анықтайды? гипербола

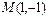нүктесі арқылы және 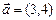векторына перпендикуляр өтетін түзудің теңдеуін жазыңыз 4y+3x+1=0

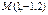нүктесінен 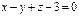жазықтығына дейінгі арақашықтықты табыңыз 1\√3

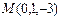нүктесі арқылы және 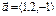векторына параллель өтетін түзудің теңдеуін жазыңыз x=y-1\2=z+3\-1

Мына түзулердің қайсысы 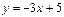түзуіне параллель? -3x+8

Мына теңдеулердің қайсысы эллипстің теңдеуі: б)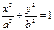

Мына теңдеулердің қайсысы гиперболаның теңдеуі: в)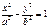

Мына теңдеулердің қайсысы параболаның теңдеуі: г)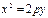

Мына теңдеулердің қайсысы шеңбердің теңдеуі: а)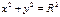

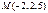нүктесі арқылы 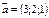векторына параллель өтетін түзудің канондық теңдеуін жазыңыз x+2\3=y-2\2=z-5\1

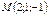нүктесі арқылы 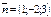векторына перпендикуляр өтетін жазықтықтың теңдеуін жазыңыз x-2y+3z+3=0

Н Н Н Н Н Н Н Н Н Н

Нүктеден түзуге дейінгі қашықтық қайсы формуламен есептелініледі: d=Ax₀₊By₀+C\√A²+B²

Нүктеден жазықтыққа дейінгі қашықтық қай формуламен есептелініледі: d=|Ax₀+By₀+Cz₀+D|\√A²+B²+C²

О О О О О О О О О О

ОХ осімен 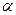бұрышын жасайтын 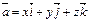векторы үшін мына формула орындалады cosα=x\√x²+y²+z²

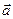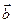Ортақ бір нүктеден шығатын және векторларына салынған параллелограмның ауданы тең |a*b|

Ох өсіне симметриялы орналасқан параболаның теңдеуін көрсет y²=2px

Оу өсіне симметриялы орналасқан параболаның теңдеуін көрсет x²=2py

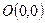нүктесінен 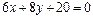түзуіне дейінгі арақашықтықты табыңыз 2

П П П П П П П П П П

Пирамиданың төбелері 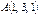, , 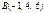, 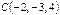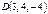нүктелерінде орналасқан. Осы пирамиданың көлемін табыңыз 3

Параметрлік теңдеумен берілген 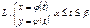сызықтарымен қоршалған жазық фигураның ауданы былай есептелінеді: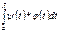

Р Р Р Р Р Р Р Р Р Р Р

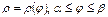сызықтарымен қоршалған жазық фигураның ауданы былай есептелінеді: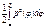

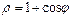сызығымен қоршалған жазық фигураның ауданын есептеу керек 3π\2

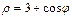сызығымен қоршалған жазық фигураның ауданын есептеу керек 19π\2

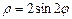сызығымен қоршалған жазық фигураның ауданын есептеу керек π\2

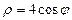сызығымен қоршалған жазық фигураның ауданын есептеу керек 4π

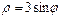сызығымен қоршалған жазық фигураның ауданын есептеу керек 9π\4

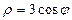қисығының доғасының ұзындығын есептеу керек 3π

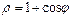қисығының доғасының ұзындығын есептеу керек 8

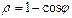қисығының доғасының ұзындығын есептеу керек 8

С С С С С С С С С

Скаляр көбейтінді үшін келесі теңдік орындалады (a,b+c)=(a,b)+(a,c)

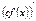туындысының формуласын көрсетіңіз: cf^,(x), мұндағы с тұрақты

Т Т Т Т Т Т Т Т Т Т

Теңдеуді шешіңіз 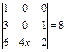Ж:2

Теңдеуді шешіңіз 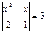Ж:

Теңдеуді шешіңіз 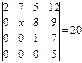Ж:2

Теңдеуді шешіңіз 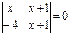Ж(-4;-1)

Теңдеуді шешіңіз 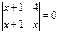Ж: (-1;4)

Теңдеуді шешіңіз 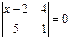Ж:22

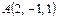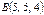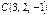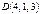Тетраэдрдің төбелері , , және нүктелерінде орналасқан. Осы тэтраэдрдің көлемін есептеңіз

Түзудің жалпы теңдеуін көрсет Ax+By+C=0

Түзудің кесінділік теңдеуін көрсет x\a+y\b=1

Түзудің параметрлік теңдеуін көрсет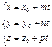

Түзудің канондық теңдеуін көрсет x-x₀\m=y-y₀\n=z-z₀\p

Төмендегі теңдіктердің қайсысы 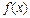функциясының қандай да бір 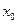нүктесіндегі үзіліссіздікті көрсетеді? lim

Туындыны табыңыз: 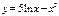5\x-2x

Туындысы арқылы функцияның өсу аралығын табыңыз: 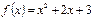[-1;∞)

Туындысы арқылы функцияның өсу аралығын табыңыз: 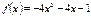(-∞;-1\2)

Туындысы арқылы функцияның өсу аралығын табыңыз: (-∞;∞)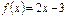

Туындысы арқылы функцияның өсу аралығын табыңыз: 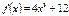[0;∞)

Туындысы арқылы функцияның өсу аралығын табыңыз: 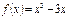(-∞;-1)U[1;∞)

У У У У У У У У У

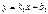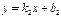және түзулерінің перпендикулярлық белгісін көрсет k₁k₂=1

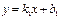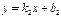және түзулерінің параллельдік белгісін көрсет k₁=k₂

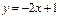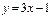және түзулерінің арасындағы сүйір бұрышты табыңыз 45⁰

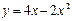параболасының төбесінің координаталарын табыңыз (1;2)

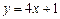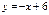және түзулерінің қиылысу нүктелерінің координаталарын табыңыз (1,5)

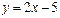және 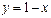түзулерінің қиылысу нүктелерінің координаталарын табыңыз (2;-1)

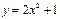функцияның анықталу облысын көрсетіңіз: (-∞;∞)

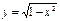функциясының анықталу облысын көрсетіңіз:[-1;1]

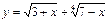функцияның анықталу облысын көрсетіңіз:[-3;7]

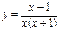функциясының үзіліс нүктесін көрсетіңіз: x=0,x=-1

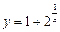функциясының үзіліс нүктесін табыңыз: х=0

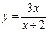функцияның үзіліс нүктесін және оның типін анықтаңыз: x=-2 π типті үзіліс

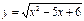функциясының анықталу облысын табыңыз: (-∞;2]U[3;∞)

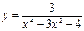функциясының үзіліс нүктесін табыңыз x₁=2, x₂=-2

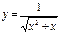функциясының үзіліс нүктесін табыңыз:x₁=0, x₂=-1

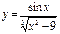функциясының үзіліс нүктесін табыңыз:x₁=3, x₂=-3

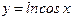функциясының анықталу облысын табыңыз:2πn-π\2<x<π\2+2πn

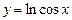функциясының мендер облысын табыңыз: y€(-∞;0)

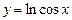функциясының периодын табыңыз: T=2π

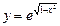функциясының анықталу облысын табыңыз: -1≤x≤1

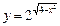функциясының мәндер облысын табыңыз: 1≤y≤4

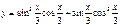функциясының периодын табыңыз:T=3π

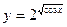функциясының периодын табыңыз: T=2π

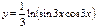функциясының периодын табыңыз: T=π\3

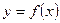функциясының 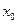нүктесiнде туындысы деп нені айтады? f^,(x₀)=limf(x₀+x)-f(x₀)\x

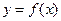функциясының 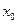нүктесiнде экстремумы болуы үшiн оның осы нүктедегi туындысы неге тең болады? нөлге тең (f^,(x₀)=0) н\е болмайды

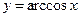функциясының туындысын көрсетіңіз: -1\√1-x²

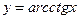функциясының туындысын көрсетіңіз: -1\1+x²

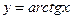функциясының туындысының формуласын көрсетіңіз 1\1+x²

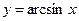функциясының туындысының формуласын көрсетіңіз: 1\√1-x²

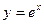функциясының туындысы неге тең? e^x

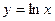функциясының туындысы неге тең? 1\x

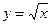функциясының туындысы неге тең? 1\2√x

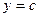туындысы, мұнда с-тұрақты 0

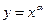туындысы неге тең? ax^a-1

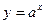туындысы неге тең? a^xlna

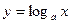туындысы неге тең? 1\xlna

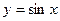туындысы неге тең? cosx

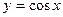туындысы неге тең? -sinx

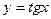туындысы неге тең? 1\cos²x

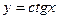туындысы неге тең? -1\sin²x

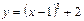функциясының иілу нүктесін табыңыз: (1;2)

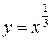функциясының иілу нүктесін табыңыз: (0;0)

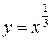функциясының кему аралығын табыңыз: (-∞;0)

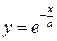функциясының 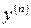табыңыз: (-1\a)^ae^-x\a

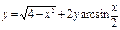функциясының туындысы 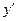-ті табыңыз: √2-x\√2+x