Розв'яжіть завдання 2.1 - 2.4. Запишіть відповідь у бланк відповідей.
2.1. Розв'яжіть систему рівнянь 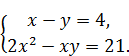
2.2. Чому дорівнює другий член нескінченної геометричної прогресії, сума і знаменник якої дорівнюють відповідно 72 і 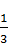 ?
?
2.3. Спростіть вираз 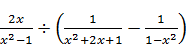
2.4. Знайдіть кут А трикутника ABC, якщо ВС = 7 см, АС = 3 см, АВ = 8 см.
Частина третя
Розв'язання задач 3.1 - 3.4 повинно мати обґрунтування. У ньому потрібно записати послідовні логічні дії та пояснення, зробити посилання на математичні факти, з яких випливає те чи інше твердження. Якщо потрібно, проілюструйте розв'язання схемами, графіками, таблицями.
3.1. Складіть квадратне рівняння, корені якого більші за відповідні корені рівняння х2 + 4х - 9 = 0 на одиницю.
3.2. Турист проплив на моторному човні 25 км проти течії річки і повернувся назад на плоту. Знайдіть швидкість течії річки, якщо на плоту турист плив на 10 год більше, ніж на човні, а власна швидкість човна становить 12 км/год.
1.9. Центр кола, описаного навколо чотирикутника ABCD, належить його стороні AD. Знайдіть кути даного чотирикутника якщо 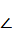 ACB = 30°,
ACB = 30°, 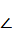 CBD =20°.
CBD =20°.
Варіант 23
Частина перша
Завдання 1.1-1.12 мають по чотири варіанти відповідей, з яких тільки ОДНА відповідь ПРАВИЛЬНА. Оберіть правильну, на Вашу думку, відповідь та позначте її у бланку відповідей.
1.1. Обчисліть значення виразу 4,2: (-0,6) +1,2.
А) 1,9; Б)-5,8; В) 0,5; Г) -1,9.
1.2. Спростіть вираз 12 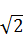 -
- 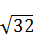
А)6 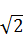 ; Б) 8
; Б) 8 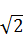 ; В) 4
; В) 4 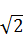 ; Г) 12
; Г) 12 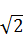 .
.
1.3. Знайдіть суму десяти перших членів арифметичної прогресії, перший член якої а1 = - 4, а різниця d = 6.
А) 230; Б) 240; В) 260; Г) 310.
1.4. Відомо, що а>b. Яка з нерівностей хибна?
А) а - 0,4 > b - 0,4 ; В) а + 0,4 > b + 0,4;
Б) 0,4а > 0,4b ; Г) - 0,4а > - 0,4b .
1.5. Виконайте додавання: 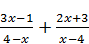
А)-1; Б) 1; В) 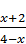 ; Г)
; Г) 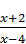 .
.
1.6. Визначте формулу оберненої пропорційності, якщо її графіку належить точка А (-3; 6).
А)y= 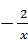 ; Б) y=
; Б) y= 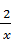 ; В) y=
; В) y= 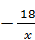 ; Г) y=
; Г) y= 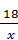
1.7. На рисунку зображено графік руху туриста. З якою швидкістю йшов турист до місця відпочинку?
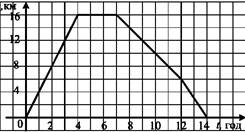 |
А) 16 км/год; Б) 8 км/год; В) 6 км/год; Г) 4 км/год.
1.8. У Дмитра є 10 купюр по 5 грн, а у Миколи — 10 купюр по 2 грн. Скільки купюр має віддати Дмитро Миколі, щоб у них стало порівну грошей?
А) 2 купюри; Б) 3 купюри; В) 4 купюри; Г) 5 купюр.
1.9. Яка з нерівностей є правильною?
A) sinl30°cosl00° > 0; В) sinl30°cosl00° < 0;
Б) sinl30°cos20° < 0; Г) sinl30°cos90° > 0.
1.10. Яку частину площі круга становить площа сектора, градусна міра дуги якого дорівнює 72°?
А) 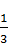 Б)
Б) 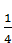 ; В)
; В) 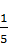 ; Г)
; Г) 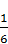 .
.
1.11. Чому дорівнює більша із сторін паралелограма, якщо вона на 8 см більша за іншу сторону, а периметр паралелограма дорівнює 40 см?
А) 20 см; Б) 18 см; В) 16 см; Г) 14 см.
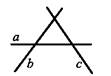 1.12. Яка з прямих, зображених на рисунку, є образом прямої b при паралельному перенесенні?
1.12. Яка з прямих, зображених на рисунку, є образом прямої b при паралельному перенесенні?
А) а; Б) b; В) с; Г) жодна з даних прямих.
Частина друга
Розв'яжіть завдання 2.1 - 2.4. Запишіть відповідь у бланк відповідей.
2.1. У саду ростуть яблуні і вишні, причому яблуні становлять 52 % усіх дерев. Вишень росте на 8 дерев менше, ніж яблунь. Скільки дерев росте в саду?
2.2. Знайдіть значення виразу 
2.3. Розв'яжіть нерівність (х +19) (х - 3) - (2х -1) (2х +1) > х - 38.
2.4. Складіть рівняння кола, діаметром якого є відрізок МК, якщо М(-3; 4), K(5; 10).
Частина третя
Розв'язання задач 3.1 - 3.3 повинно мати обґрунтування. У ньому потрібно записати послідовні логічні дії та пояснення, зробити посилання на математичні факти, з яких випливає те чи інше твердження. Якщо потрібно, проілюструйте розв'язання схемами, графіками, таблицями.
3.1. Знайдіть суму всіх трицифрових чисел, які кратні 7
3.2. Два автомобілі виїхали одночасно з міст А і В назустріч один одному. Через годину вони зустрілись і, не зупиняючись, продовжили рухатися з тими самими швидкостями. Один з них прибув у місто В на 50 хв пізніше, ніж інший — у місто А. Знайдіть швидкість кожного автомобіля, якщо відстань між містами становить 100 км.
3.3. У прямокутну трапецію вписано коло. Точка дотику ділить більшу з бічних сторін трапеції на відрізки завдовжки 4 см і 25 см. Знайдіть площу трапеції.
Варіант 24
Частина перша
Завдання 1.1-1.12 мають по чотири варіанти відповідей, з яких тільки ОДНА відповідь ПРАВИЛЬНА. Оберіть правильну, на Вашу думку, відповідь та позначте її у бланку відповідей.
1.1. Порівняйте числа а і b, якщо а—b = — 4,6.
А) а>b; Б) а <b; В) а = b; Г) порівняти неможливо.
1.2. Подайте у вигляді степеня вираз (b3)4 : b10.
A) b2 ; Б) b8 ; В) b4 ; Г) b6 .
1.3. Спростіть вираз 3m - 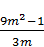
А) 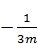 ; Б)
; Б) 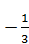 ; В)
; В) 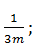 Г)
Г) 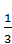
1.4. Яка множина розв'язків системи нерівностей 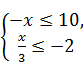
А) [-10;-6]; Б) (- 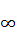 ; -6]; В)[-10;+
; -6]; В)[-10;+ 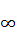 ); Г) [6; 10].
); Г) [6; 10].
1.5. Дано функцію f(x) = 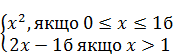 Чому дорівнює f(
Чому дорівнює f( 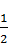 )?
)?
А) 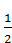 ; Б) 1; В)
; Б) 1; В) 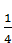 ; Г)0.
; Г)0.
1.6. Знайдіть суму нескінченної геометричної прогресії, перший член якої b1= 18, а знаменник q = 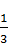 .
.
А) 12; Б) 27; В) 24; Г) 15.
1.7. Між пристанями А і В, розташованими на протилежних берегах озера, курсує пором. На рисунку зображено графік руху порома під час двох перших рейсів від пристані А до пристані В і назад. З якою швидкістю здійснював пором другий рейс від пристані А до пристані В?
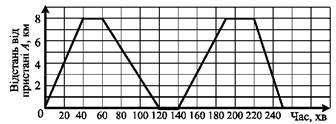 |
А) 12 км/год; Б) 10,4 км/год; В) 9,6 км/год; Г) 8 км/год.
1.8. На виставі в цирку іі усіх глядачів становили діти. Скільки відсотків усіх глядачів становили діти?
 А) 14%; Б) 2,8%; В) 5,6 %; Г) 56 %.
А) 14%; Б) 2,8%; В) 5,6 %; Г) 56 %.
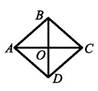
1.9. Чому має дорівнювати довжина відрізка ОС, щоб ромб ABCD, зображений на рисунку, був квадратом, якщо ВО = 8 см?
А) 2 см; Б) 4 см; В) 8 см; Г) 16 см.
1.10. Сума трьох сторін паралелограма дорівнює 24 см. Знайдіть сторони паралелограма, якщо його периметр становить 30 см.
 А) 6 см, 9 см, 6 см, 9 см; В) 7 см, 8 см, 7 см, 8 см;
А) 6 см, 9 см, 6 см, 9 см; В) 7 см, 8 см, 7 см, 8 см;
Б) 6 см, 8 см, 6 см, 8 см; Г) знайти неможливо.
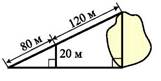
1.11. За даними, наведеними на рисунку, знайдіть ширину озера.
А) 30 м; Б) 50 м; В) 60 м; Г) 80 м.
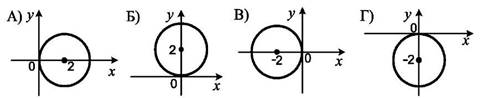
1.12. На якому рисунку зображено коло, рівняння якого має вигляд
х2 +(у + 2)2 = 4 ?
 Частина друга Розв'яжіть завдання 2.1 — 2.4. Запишіть відповідь у бланк відповідей. Частина друга Розв'яжіть завдання 2.1 — 2.4. Запишіть відповідь у бланк відповідей. |
2.1. Розв'яжіть рівняння 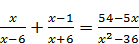
2.2. У коробці лежать зелені та блакитні кулі. Скільки у коробці блакитних куль, якщо зелених у ній 18, а ймовірність того, що обрана навмання куля
виявиться блакитною, дорівнює 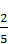 ?
?
2.3. Число -2 є коренем рівняння х2 + bх - 24 = 0. Знайдіть другий корінь рівняння і значення b.
2.4.3 точки до прямої проведено дві похилі завдовжки 10 см і 18 см, а сума їх проекцій на пряму дорівнює 16 см. Знайдіть відстань від даної точки до цієї прямої.
Частина третя
Розв'язання задач 3.1 - 3.4 повинно мати обґрунтування. У ньому потрібно записати послідовні логічні дії та пояснення, зробити посилання на математичні факти, з яких випливає те чи інше твердження. Якщо потрібно, проілюструйте розв'язання схемами, графіками, таблицями.
3.1. Знайдіть область визначення функції у = 
3.2. Стіл і стілець коштували разом 1500 грн. Після того як стіл подешевшав на 20 %, а стілець подорожчав на 20 %, вони стали коштувати разом 1320 грн. Знайдіть початкову ціну стола і початкову ціну стільця.
3.3. У трапеції ABCD відомо, що ВС || AD, AD = 8 см, CD = 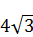 см. Коло, яке проходить через точки А, В і С, перетинає відрізок AD у точці К,
см. Коло, яке проходить через точки А, В і С, перетинає відрізок AD у точці К,  AKB = 60°. Знайдіть відрізок ВК
AKB = 60°. Знайдіть відрізок ВК
Варіант 25
Частина перша
