Уравнение состояния

Уравнение неразрывности

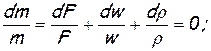
Уравнение Бернулли

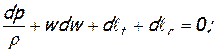
Уравнение энергии

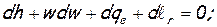
уравнение состояния

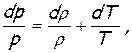
для анализа изменения скорости в результате геометрического (dF/F),расходного (dm/m), теплового (dq_e), механического (dℓ_t) воздействий и воздействия трения (dℓ_r) получим

(***)

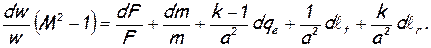«Дляего вывода в качестве исходных берутся следующие уравнения:

уравнение Бернулли (см.2.13)

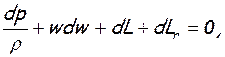(7.1)

уравнение состояния газа (1.38), которое в дифференциальной форме имеет вид:

dр= Rρdt + RТdρ, (7.2)

уравнение энергии (2.6), которое после замены 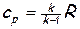может быть записано как

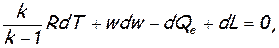(7.3)

уравнение массового расхода (1.15), которое после логарифмирования и дифференцирования приобретает вид

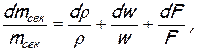(7.4)

а также формула скорости звука

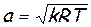(7.5)

Существо вывода состоит в том, что в уравнении (7.1) делаются замены величин, в результате которых в нем остаются только скорость, скорость звука и физические воздействия dF, dm_сек, dL, dL_r, dQ_e. Это достигается путем замены 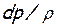в уравнении (7.1) его значением, найденным из уравнения (7.2), причем в последнем RdТ находится из уравнения (7.3), 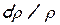из уравнения (7.4), а RТ из уравнения (7.5). Тогда уравнение (7.1) приобретает вид

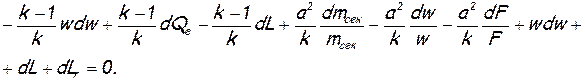
Приведя подобные члены, соберем в левую часть все величины, содержащие скорость, а в правую — физические воздействия. После сокращения обеих частей на а²/ k и замены w/a=М, получим

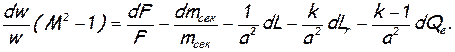(7.6)

Формула (7.6) (тоже самое, что и (***) – В.Г.) называется уравнением обращения воздействий. Оно выражает так называемый закон обращения воздействий. Согласно этому закону, для непрерывного изменения скорости газа в одну сторону за счет только одного физического воздействия необходимо, чтобы знак этого воздействия менялся на обратный в момент перехода через скорость звука. Если в процессе участвуют сразу несколько физических воздействий, то в момент перехода через скорость звука знак их суммы должен измениться на обратный. Уравнение обращения воздействия позволяет определить какой знак должно иметь то или иное воздействие для ускорения или торможения дозвуковых или сверхзвуковых потоков.

Закон обращения воздействия отражает усиливающееся влияние сжимаемости газа на его движение при увеличении числа Маха. При переходе через скорость звука (M=1) эти количественные изменения переходят в качественные – обращаются воздействия. Можно сказать, что закон обращения воздействия представляет собой пример проявления в газовой динамике более общего закона - закона перехода количества в качество.

Из уравнения обращения воздействий (7.6) легко получить пять частных случаев изменения скорости потока под влиянием какого–нибудь одного физического воздействия. Для этого в уравнении (7.6) все остальные воздействия надо положить равными нулю.

Так, например, если геометрическое воздействие dF 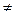0, а dМ_сек=dL=dL_r=dQ_e=0, то получается уравнение Гюгонио

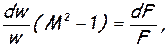
которое было подробно рассмотрено выше.

Если взять только одно расходное воздействие dm_сек 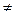0, то уравнение (7.6) приобретает такой вид:

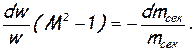(7.7)

Течение, отвечающее этому уравнению, реализуется внутри расходного сопла. Его схема дана на рисунке 131. Оно представляет собой трубу или канал постоянного сечения, имеющий на боковых стенках систему отверстий, через которые подводятся в основной поток дополнительные массы газа или отводятся из него.

Если на входе w₁<а (М₁<1) и к потоку подводится дополнительная масса газа (следовательно, расход увеличивается вдоль потока, dМ_сек>0), то для согласования знаков левой и правой части уравнения (7.7) необходимо, чтобы dw>0. Таким образом, от входа до критического сечения скорость будет нарастать. В критическом сечении М=1, значит dm_сек/m_сек=0, т.е. расход в этом сечении проходит через максимум. За критическим сечением газ отбирается, расход уменьшается вдоль потока, т.е. dm_сек<0. Так как здесь М>1, то из уравнения (7.7) получается, что dw>0.

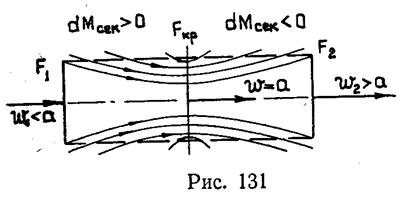
Рассматривая рис. 131, можно заметить, что основной поток, т.е. масса газа, которая поступает в канал через входное сечение F₁, имеет форму, напоминающую сопло Лаваля: сначала поток поджимается, в горле его сечение минимально, за горлом он расширяется. В отличие от геометрического сопла, в расходном поджатие основного потока происходит за счет дополнительной массы газа, которая оказывает вытеснительное действие. «Стенкой» для основного потока является в этом случае граница струи дополнительной массы газа. Изменение параметров основного потока, движущегося через расходное сопло, происходит по тем же законам, что и в случае обычного геометрического сопла.

Расходное сопло в том виде, как оно изображено на рис. 131, в технике не применяется, но его отдельные элементы встречаются довольно часто. При течении газа в смесителях, при подмешивании воздуха в зону горения в камерах сгорания, при отборе газа через отверстия в стенках канала и во многих других случаях наблюдается эффект расходного воздействия. Для получения сверхзвуковых потоков в небольших аэродинамических трубах, предназначенных для тарирования пневмометрических насадков и приборов, иногда применяют комбинированное сопло. Его дозвуковая часть представляет собой суживающееся геометрическое сопло, а сверхзвуковая — расходное сопло с отбором воздуха. Изменяя количество отбираемого воздуха, можно регулировать число М на выходе, сохраняя поток «чистым», без скачков.

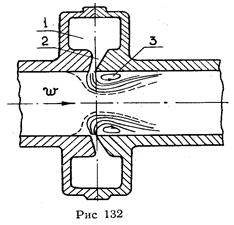
Не следует смешивать расходное сопло и сопло с аэродинамическим поджатием потока. Схема последнего изображена на рис. 132.

Из ресивера 1 через щелевые сопла 2 газ высокого давления вдувается в основной канал, где поджимает основной поток, в котором образуется «горло». Поджатие здесь получается не за счет вытеснительного действия вдуваемого газа, а за счет его кинетической энергии. Между вдуваемой струей и стенкой образуется замкнутая вихревая зона 3. Количество вдуваемого газа в этом случае получается меньше, чем дополнительная масса, подаваемая в расходное сопло, поэтому «аэродинамическое»сопло экономичнее «расходного».

С помощью уравнения обращения воздействий (7.6) можно аналогичным способом проанализировать и другие виды воздействий. Они будут рассмотрены ниже. Здесь же только отметим еще одну особенность закона обращения воздействий.

Во всех случаях, когда физическое воздействие обратимо (т.е. может менять знак на обратный), замена дозвукового входящего потока на сверхзвуковой приводит к тому, что сверхзвуковое сопло обращается в сверхзвуковой диффузор (см. например, для случая геометрического воздействия .

Режимы течения газа в канале, имеющем горло

Каналы, имеющие сужение между входным и выходным сечениями, или горло, довольно широко применяются в технике. Они используются как сопла Лаваля для получения сверхзвуковых потоков, как диффузоры для преобразования сверхзвуковых потоков в дозвуковые, как трубки Вентури, служащие в качестве датчиков измерительных устройств и систем регулирования. При этом один и тот же канал может быть и соплом Лаваля, и трубкой Вентури, и сверхзвуковым диффузором в зависимости от того, какие условия созданы на входе и выходе. Рассмотрим это более подробно.

На рисунке 24 изображена схема такого канала и графики изменения скорости и давления по его длине. Площади поперечного сечения канала на входе и на выходе приняты одинаковыми, течение — энергоизолированным изоэнтропным. От входного сечения 1 до горла Г площадь сечения уменьшается, т.е. dF<0, в горле она проходит через минимум dF=0, от горла до сечения 2 — увеличивается, т.е. dF>0. Применяя уравнение Гюгонио (2.77), можно заключить, что здесь возможны четыре режима течения.

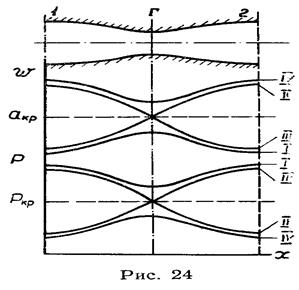
1. Если поток на входе дозвуковой, М<1, то, согласно уравнению (2.77), в суживающейся части скорость должна нарастать (dw>0). Если в сечении горла скорость еще не достигла критической, то поток, выйдя в расширяющуюся часть, оставаясь дозвуковым, будет двигаться там с уменьшением скорости и ростом давления, как в обычном дозвуковом диффузоре. Этому режиму отвечают кривые 1 на рисунке 24. В этом случае канал работает как трубка Вентури.

2. Условия на входе те же, но в сечении горла скорость достигает критического значения, т.е. М=1, переходит его и становится сверхзвуковой. Тогда, согласно уравнению (2.77), в расширяющейся части канала при М>1 скорость должна нарастать. Кривые II на рисунке 24 показывают, что по всей длине происходит увеличение скорости и уменьшение давления. Поток из дозвукового превращается в сверхзвуковой. На этом режиме канал работает как сопло Лаваля.

3. В канал входит сверхзвуковой поток, т.е. М>1. На основании анализа уравнения (2.77) имеем, что в суживающейся части скорость должна уменьшаться. Если в сечении горла она достигнет критического значения (М=1) и перейдет его, то в расширяющуюся часть поступает дозвуковой поток. Следовательно, от горла до сечения 2 течение происходит как в обычном дозвуковом диффузоре — с уменьшением скорости и ростом давления. Этому режиму соответствуют кривые III (см. рисунок 24), которые показывают, что на всем протяжении потока скорость уменьшается, а давление нарастает. Канал работает как диффузор и называется сверхзвуковым диффузором.

4. Условия на входе такие же, как в предыдущем режиме, но в сечении горла скорость еще не достигает критической, а остается сверхзвуковой — М>1. С этой скоростью поток минует горло и выходит в расширяющуюся часть. В соответствии с уравнением (2.77), при М>1 и dF>0 скорость будет нарастать, а давление — падать. Таким образом, кривые распределения скорости и давления IV получаются симметричными первому случаю. Специального названия этот режим не имеет. В действительных условиях он реализуется лишь частично: от входного сечения до горла и на некотором расстоянии за горлом течение происходит в соответствии с кривыми IV, но затем возникает ударная волна и движение перестраивается — поток становится дозвуковым.

Если сопоставить между собой первый и второй режимы то можно заметить, что причина их различия заключается в том, достигнет ли скорость в сечении горла критического значения или не достигнет. Это определяет дальнейшую судьбу потока: станет ли он сверхзвуковым или останется дозвуковым. Анализ уравнения (2.77) не дает ответа на этот вопрос. Ответ можно получить, рассматривая уравнение неразрывности

ρ₁ w₁ F₁ = ρ_Г w_Г F_Г ,

которое после деления обеих частей на ρ_кр а_кр и использования формулы (2.78) принимает вид

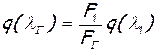(2.85)

и выражается графически на рисунке 23[3]. Пусть, например, отношение площадей F₁/F₂=2. Если на входе в канал λ₁=0,2, то, как это следует из рисунка 23, q(λ)=0,31. Согласно уравнению (2.85), имеем 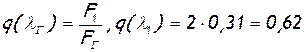. При этом значении λ_Г=0,44, т.е. λ_Г<1, поэтому канал будет работать как трубка Вентури. Если увеличить расход газа через канал, то увеличится и скорость во входном сечении. При λ₁=0,34 приведенный расход получается q(λ₁)=0,5. Тогда по формуле (2.85) находим q(λ_Г)=1, следовательно, λ=1, т.е. канал может работать как сопло Лаваля.

Чтобы уяснить, какие же изменения надо произвести в условиях на сходе и выходе канала, чтобы перейти от первого режима ко второму, достаточно посмотреть на кривые давлений I и II. В трубке Вентури разность давлений на входе и выходе равна нулю. (В реальных условиях для преодоления потерь на трения необходим небольшой перепад давлений.) В случае сопла Лаваля на концах канала должен быть приложен значительный перепад давлений.

Кривые, построенные на рисунке 24, относятся к так называемым расчетным режимам. На этих режимах скорости и давления полностью соответствуют площадям поперечных сечений канала. Так, например, при заданных условиях на входе у сопла Лаваля с определенным отношением площадей выходного сечения и горла может быть лишь одно вполне определенное значение скорости истечения и одно вполне определенное значение давления на выходе. Если давление той среды, в которую происходит истечение, не равно расчетному, то возникает нерасчетный режим. На нерасчетном режиме давление на срезе сопла (т.е. в выходном сечении 2) может оставаться более высоким, чем в окружающей среде. Могут быть и такие нерасчетные режимы, при которых внутри сопла появляется ударная волна, и скорость истечения получается ниже расчетной.

Течение с трением

Трубы и каналы постоянного поперечного сечения, как круглой, так и фасонной формы, весьма часто применяются в теплоэнергетических установках. Если такой канал неподвижен и теплообмен через стенки отсутствует, то задача его расчета сводится к определению параметров потока газа, движущегося в цилиндрической трубе с трением без внешнего теплообмена. В уравнении (7.6) в этом случае нужно учитывать только воздействие трением. Тогда

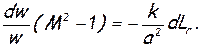(7.8)

Из уравнения (7.8) легко устанавливается влияние трения на скорость потока. Поскольку всегда dL_r>0, то при М<1 получается dw>0, а при М>1 dw<0, т.е. в дозвуковом потоке скорость за счет трения возрастает, а в сверхзвуковом — уменьшается [4].

Для выполнения расчетов формула (7.8) неудобна. Ее следует преобразовать, сделав следующие замены. Число Мнужно выразить через приведенную скорость λ по формуле (2.55)

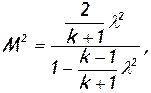
отношение dw/w представить как dw/w=dλ/λ, поделив числитель и знаменатель на критическую скорость а_кр, а работу гидравлических потерь dL_r выразить с помощью известной в гидравлике формулы путевых потерь

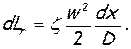
Заметим, что в энергоизолированном течении, к которому относится рассматриваемая задача, в силу постоянства температуры торможения критическая скорость сохраняет постоянное значение вдоль всего потока (поэтому ее можно вносить под знак производной). Величины dх и D, входящие в формулу работы трения, представляют элементарную длину трубы и ее диаметр. В случае некруглого поперечного сечения вместо геометрического берется гидравлический диаметр, равный отношению учетверенной площади поперечного сечения к смоченному периметру. Коэффициент путевых потерь, иначе называемый коэффициентом сопротивления трубы, зависит от числа Рейнольдса Rе=wD/ν и относительной шероховатости D/k_Э, — где k_Э— средняя высота бугорков на обтекаемой поверхности.

Сделав соответствующие подстановки в формулу (7.8), получим дифференциальное уравнение с разделенными переменными

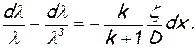\(7.9)

Это уравнение легко интегрируется при ζ=соnst. В противном случае решение приходится вести численным методом, так как зависимость ζ=ζ(x) не выражается в аналитическом виде. Обратимся к экспериментальным данным.

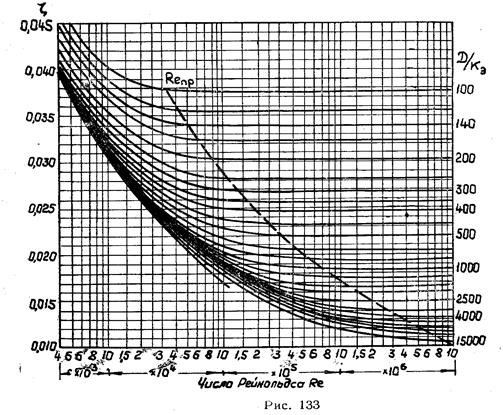
На рис. 133 приведены результаты испытаний большого количества труб с различной относительной шероховатостью, проведенных во всесоюзном теплотехническом институте Г.А.Муриным. Кривые представляют зависимость коэффициента сопротивления круглой трубы от числа Рейнольдса при заданной шероховатости. Из графиков видно, что для одной и той же трубы (т.е. при одной и той же шероховатости) с ростом числа Рейнольдса коэффициент сопротивления падает, но, начиная с некоторого значения Rе=Rе_пр, он сохраняется постоянным. Правее линии, обозначенной Rе_пр, лежит так называемая автомодельная область. В этой области число Рейнольдса уже не влияет на коэффициент сопротивления, и он зависит только от относительной шероховатости. Как показывают подсчеты чисел Рейнольдса, в большинстве задач, встречающихся в теплоэнергетической практике, значения Rе превышают предельные, что дает право считать ζ=соnst для данного канала. Тогда, интегрируя уравнение (7.9) в пределах от λ₁ до λ₂ и от 0 до х, получим

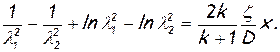
Сгруппируем в левой части величины с одинаковыми индексами, а в правой обозначим

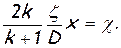(7.10)

Величина χ называется приведенной длиной трубы. Она включает в себя, кроме физической длины и диаметра, еще коэффициент сопротивления и показатель изоэнтропы газа, следовательно, обобщает все индивидуальные особенности течения. После небольших преобразований уравнение движения газа в трубе приобретает следующий вид:

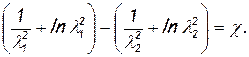(7.11)

Функции 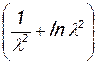вычисляются для всех значений λ и сводятся в таблицы. С применением таких таблиц уравнение (7.11) решается очень просто.

На рисунке 134 построены графики, рассчитанные по формуле (7.11). Пользуясь такими графиками, можно по заданной приведенной скорости на входе в трубу легко найти λ в любом сечении, для которого известна приведенная длина. Следует обратить внимание, что кривые имеют максимум по χ. Проверив функцию (7.11) на экстремум, нетрудно убедиться, что максимум получается именно при χ=1. Существование этого максимума говорит о том, что заданные условия течения могут реализоваться в трубе не более определенной конечной длины, при достижении которой наступает так называемый кризис течения.

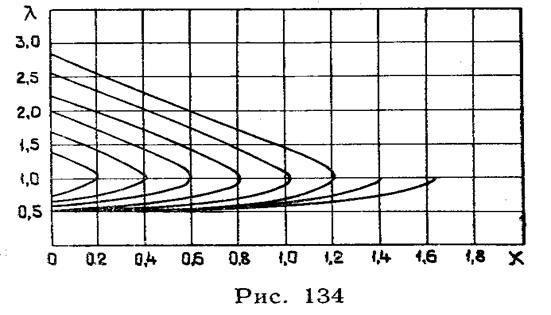
Кризисом течения называется такой режим, при котором на выходе из трубы устанавливается скорость течения, равная критической. Длина трубы, соответствующая кризису течения, называется критической длиной трубы. Ее приведенная величина χ_кр получается из уравнения (7.11), после подстановки λ₂=1, а именно:

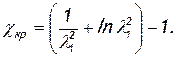(7.12)

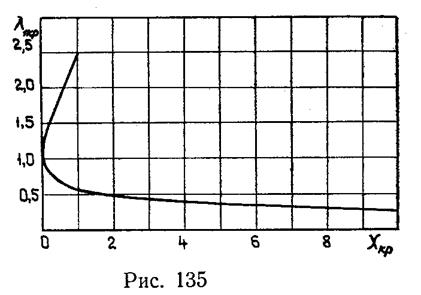
При кризисе течения расход газа через трубу достигает наибольшего возможного значения, а скорость на входе (при дозвуковом течении) не может быть больше той, которая получается на этом режиме. Из рассмотрения кривых на рисунке 134 следует, что чем короче труба, тем большую величину имеет λ_1кр; при χ=0, т.е. когда труба превращается в отверстие, λ_1кр=1. Соответствующий график изображен на рис. 135.

Рассмотрим возможные режимы течения газа по трубе. Если по трубе длиной х пропускать газ с небольшой начальной скоростью, то установится докритический режим течения, которому на рисунке 136 отвечает кривая 1. Скорость на этом режиме возрастает по длине трубы, а давление — падает. Увеличивая расход через трубу, можно повысить скорости во всех ее сечениях. Это повышение возможно лишь до тех пор, пока скорость на выходе не достигнет критической, т.е. не установится кризис течения. Кривая, соответствующая критическому режиму при дозвуковом течении в трубе, обозначена на рисунке 136 цифрой II. Здесь также скорость по длине трубы возрастает. Дальнейшее увеличение расхода через трубу невозможно. Если предположить, что каким-то путем удалось это сделать, то кривая приведенной скорости поднимется и займет положение III. Рассматривая эту линию, видим, что уже где–то в середине трубы λ=1, т.е. скорость должна перейти через скорость звука. Такой переход невозможен, так как согласно уравнению (7.8) работа трения должна была бы изменить свой знак на обратный. Следовательно, если бы режим III даже и возник, то он не мог бы существовать сколь–либо продолжительное время: расход через трубу, а значит и скорости во всех ее сечениях стали бы уменьшаться до тех пор, пока критическое сечение не переместилось в выходное сечение трубы, т.е. кривая не заняла бы положение II.

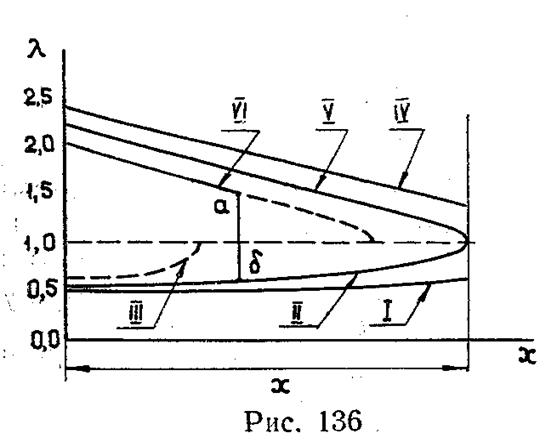
Представим себе теперь, что в трубу подается сверхзвуковой поток газа со скоростью, соответствующей начальной точке кривой IV. Согласно уравнению (7.8), скорость по длине трубы будет уменьшаться, а давление, поэтому будет возрастать. Это — сверхкритический режим течения. Уменьшая скорость на входе, можно этот режим перевести в сверхзвуковой критический, изображенный кривой V. Дальнейшее уменьшение входной скорости (начало кривой VI) приводит к такому режиму, на котором непрерывное течение становится невозможным, так как опять критическое сечение должно получиться в середине трубы. Поэтому возникает скачок уплотнения. Таким образом, поток проходит начальный участок трубы со сверхзвуковой скоростью. В некотором сечении появляется прямой скачок уплотнения аб, за которым течение становится дозвуковым. Оставшийся участок пути дозвуковой поток проходит с увеличением скорости до критического значения на выходе, т.е. по кривой II. Скачок сам выбирает себе место: он располагается в том сечении, где выполняется кинематическое соотношение λ_а λ_β=1.

Опыты, проведенные с трубами, показывают, что в реальных условиях вместо прямого скачка возникают сложные конфигурации косых скачков, растянутые по длине потока. Однако, если не интересоваться их протяженностью, то расчеты можно вести, основываясь на модели прямого скачка.

Термодинамический процесс, соответствующий непрерывному течению газа в трубе, является довольно сложным. Он не описывается ни одним из обычно применяемых уравнений термодинамики. Условно его можно записать уравнением политропы, считая, однако, показатель политропы величиной переменной. Если обычное уравнение политропы

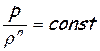или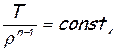

записать в дифференциальной форме

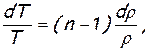(7.13)

то, считая далее показатель политропы n величиной переменной, можно найти закон его изменения по длине трубы в зависимости от местного числа М. Для этого дополнительно используются уравнение неразрывности ρw=соnst и формула температуры торможения Т*=Т+w²/[2Rk/(k–1)]. После дифференцирования при Т*=соnst (так как течение энергоизолированное) эти формулы приобретают вид

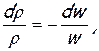(7.14)

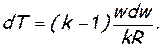(7.15)

Подставив в уравнение (7.13) значения 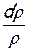и dТ, найденные из формул (7.14) и (7.15), учитывая, что kRТ=а², получим следующую зависимость показателя политропы от числа М:

n =1+(k – 1)M². (7.16)

Анализируя зависимость (7.16), нетрудно установить, как изобразится этот процесс в диаграмме ТS. Действительно, если представить дозвуковое течение в начале очень длинной трубы, где скорость весьма мала, т.е. М 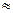0, то из уравнения (7.16) получаем, что n 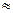1. Это соответствует процессу Т=соnst. Таким образом, при очень малых скоростях течение очень близко к изотермному (см. участок политропы вблизи точки 1 на рис. 137). По мере увеличения скорости, политропа все более отклоняется от изотермы. Когда скорость достигает критической и М=1, то n=k. Следовательно, касательная, проведенная к политропе, будет в этой точке вертикальной (точка 2 на рис.137), а процесс в критическом сечении (на выходе из трубы) будет изоэнтропным. При сверхзвуковом течении в трубе с очень большой скоростью процесс близок к изохорному (v=соnst), так как если М 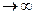, то n 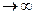. Нижняя ветвь кривой на рис. 137 относится к сверхзвуковому течению. Направления, в которых может идти процесс, указаны стрелками. Непрерывный переход через скорость звука внутри трубы, т.е. переход через точку 2 на диаграмме, невозможен, так как при этом энтропия должна перейти через максимум и в дальнейшем уменьшаться, что противоречит второму закону термодинамики.

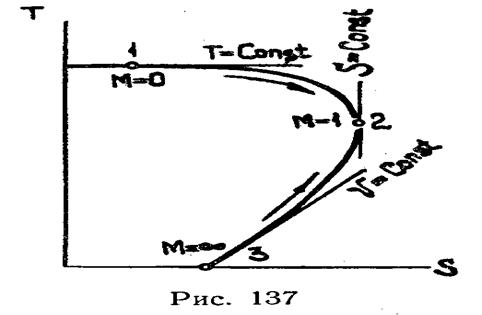
На рисунке 138 построены TS–диаграммы для дозвукового (слева) и сверх­звукового (справа) течения в трубе. Они дают наглядное представление о том, как в этих случаях распределяется энергия и как изменяется давление торможения.

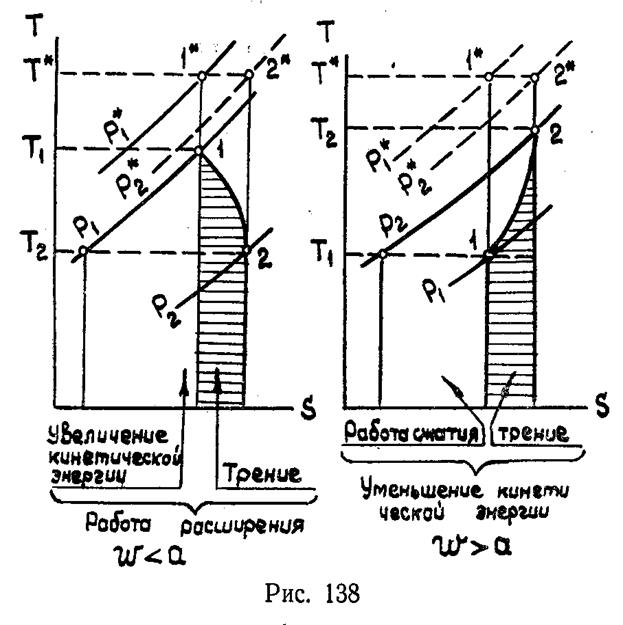
При М<1 скорость по длине трубы за счет трения возрастает. При этом падает статическое давление, т.е. газ расширяется. Работа расширения газа (вся площадь диаграммы) идет, во–первых, на увеличение кинетической энергии потока (незаштрихованная часть) и, во–вторых, на преодоление трения (горизонтально–заштрихованная часть). Давление торможения, как это следует из диаграммы, уменьшается по длине трубы, р₂*<р₁*.

При М>1 скорость потока по длине трубы за счет трения падает, т.е. уменьшается кинетическая энергия. Эта «освободившаяся» энергия изображается на рисунке138 справа всей площадью фигуры. Часть ее (незаштрихованная площадь) идет на сжатие газа, другая часть (горизонтально–заштрихованная площадка) — на преодоление трения. Давление торможения по длине трубы падает, р₂*<р₁*, несмотря на то, что статическое давление увеличивается.

Если приведенные скорости во всех сечениях трубы рассчитаны, то определение параметров состояния газа производится просто. Так как температура торможения постоянна, то истинная температура легко находится с помощью газодинамической функции τ(λ), а именно

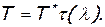(7.17)

Давление торможения и статическое давление рассчитываются по формулам

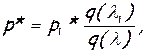(7.18)

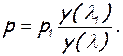(7.19)

Эти формулы получаются путем приравнивания массового расхода на входе и выходе из трубы, записанного по формулам (2.81) и (2.83), при условии Т*=соnst, m=соnst, F=соnst.

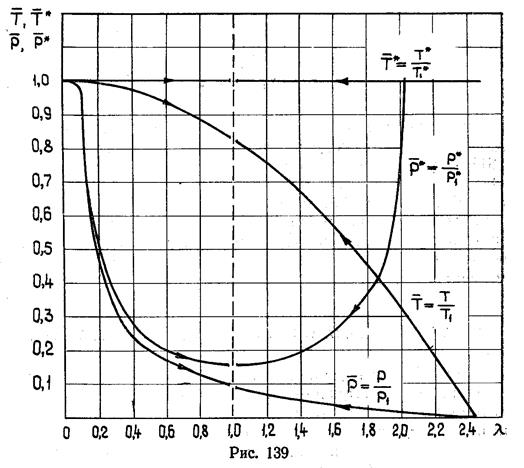
Графики зависимости параметров состояния газа от приведенной скорости, рассчитанные по этим формулам, приведены на рисунке 139. Разрыв кривых при λ=1 имеет не математический, а физический смысл: процесс не допускает непрерывный переход через λ=1, а идет только в направлении, указанном стрелками.

Течение газа с подводом и отводом тепла

Течение газа с подводом тепла извне или с отводом тепла во внешнюю охлаждающую среду довольно часто встречается в теплоэнергетических установках. В качестве примеров можно привести течение газа в теплообменниках, в камерах сгорания, в испарителях и т.п. В теплообменниках охлаждающий и охлаждаемый (или нагревающий и нагреваемый) агенты находятся по разные стороны от разделяющей твердой поверхности — стенки трубы или канала, следовательно, тепло подводится или отводится через стенку. В камерах сгорания подводимое к газу тепло вносится в поток в скрытом виде — в форме химической энергии впрыскиваемого топлива. Поэтому, несмотря на то, что процесс выделения тепла происходит в самом потоке, это тепло, по отношению к поступающему в камеру газу, является внешним. В испарительных устройствах, где в поток газа впрыскивается вода или другая жидкость (например, для понижения температуры газов), тепло, затрачиваемое на испарение, берется от самого газа. Следовательно, оно может рассматриваться, как тепло, отведенное во внешнюю среду.

Все эти виды течения можно схематизировать в виде движения газа по трубе с внешним теплообменом. Желая изучить особенности данного течения в чистом виде, нужно отбросить все другие воздействия, кроме теплового, т.е. положить, что труба цилиндрическая, неподвижная и что трение отсутствует. Обращаясь к уравнению обращения воздействий (7.6), можно записать его для этого частного случая в следующем виде:

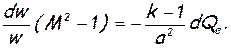(7.20)

Из формулы (7.20) следует, что в дозвуковом потоке (М<1) подвод тепла (dQ_e>0) вызывает рост скорости (dw>0), а в сверхзвуковом (М>1) — ее падение (dw<0). Отвод тепла (dQ_e<0) в дозвуковом потоке (М<1) приводит к уменьшению скорости (dw<0), а в сверхзвуковом (М>1) — к ее увеличению (dw>0).

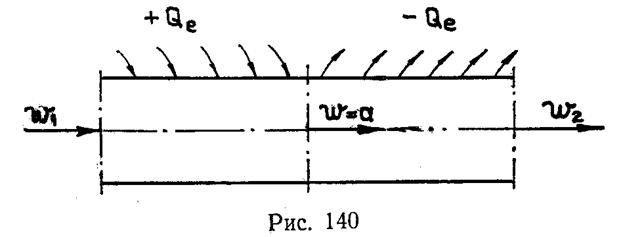
Если в начальном участке трубы подводить тепло, а затем, отводит, то можно получить так называемое тепловое сопло. Его схема изображена на рис.140. Это сопло преобразует дозвуковой поток в сверхзвуковой. Критическое сечение получается в том месте, где меняется направление теплового потока (в самом критическом сечении тепловой поток равен нулю). Если в такой канал подать сверхзвуковой поток, то его скорость будет понижаться, т.е. канал будет работать как сверхзвуковой диффузор.

Термодинамический процесс, происходящий в газе, протекающем по тепловому соплу, обладает такими же особенностями, как и в случае течения по цилиндрической трубе с трением, — он непрерывно изменяется при переходе от сечения к сечению.

Взяв уравнение политропы p/ρⁿ=const и записав его в дифференциальной форме

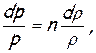(7.21)

можно применить его к исследованию данного процесса, положив, что показатель политропы n — величина переменная. Для установления зависимости n=f(М), используем еще уравнение неразрывности (7.14)

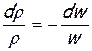
и уравнение Бернулли. Последнее для данного вида течения (L=0, L_r=0) записывается формулой (2.24), которую можно представить так:

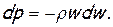(7.22)

Подставляя значения dр и 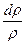, найденные из формул (7.22) и (7.14), в уравнение (7.21), учитывая при этом, что p/ρ=a²/k, получим после небольших преобразований

n = k M² . (7.23)

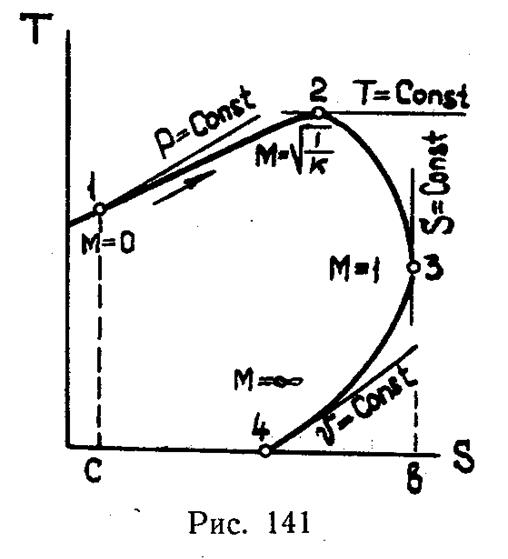
Рассмотрим характерные точки этого термодинамического процесса. Если скорость потока очень мала, т.е. М→0, то n→0. Процесс близок к изобарному (в точке М=0, изобара и линия термодинамического процесса теплового сопла имеют общую касательную). На рис. 141 этому соответствует точка 1. Если 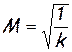, то n=1. В данной точке 2 (рис. 141) получается элементарный изотермический процесс. Если скорость потока равна критической, т.е. М=1, то n=k, т.е. в критическом сечении получается элементарный изоэнтропный процесс (точка 3, рис.141). При М 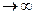показатель политропы также стремится к бесконечности, следовательно, процесс приближается к изохорному. На рис. 141 верхняя ветвь кривой 1-2-3 отвечает дозвуковому участку сопла, а нижняя — 3–4 — сверхзвуковому. Рост энтропии на дозвуковой ветви кривой связан с внешним теплопроводом; количество подведенного тепла определяется площадью а123b. Уменьшение энтропии на сверхзвуковой ветви кривой связано с отводом тепла. Количество отведенного тепла изображается площадью b34.

Изменение температуры на дозвуковом участке теплового сопла носит довольно своеобразный характер. При малых скоростях 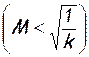подвод тепла к газу сопровождается ростом температуры, но при больших дозвуковых скоростях 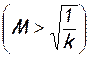— падением температуры. Этот, кажущийся парадоксальным, факт объясняется тем, что на участке сопла, где 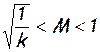, нарастание скорости происходит настолько интенсивно, что рост кинетической энергии уже не компенсируется внешним теплоподводом, в результате чего энтальпия газа начинает уменьшаться, следовательно, уменьшается и температура.

Из уравнения энергии, записанного для рассматриваемого течения (dL=0)

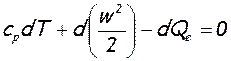
или

c_р dT^*= dQ_e , (7.24)

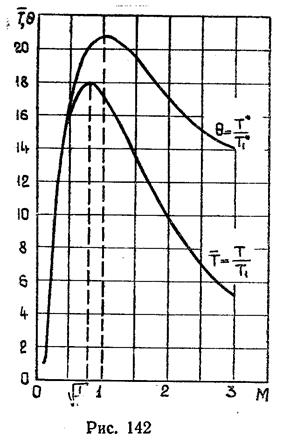
следует, что подвод тепла (dQ_e>0) вызывает рост температуры торможения, а отвод (dQ_e<0) — уменьшение. Таким образом, на дозвуковом участке теплового сопла температура торможения возрастает, в критическом сечении достигает максимума, на сверхзвуковом участке — уменьшается. Максимумы температуры торможения и термодинамической температуры не совпадают: они получаются при разных числах М. Графики изменения Т* и Т в зависимости от числа М для тепловогосопла приведены на рис. 142.

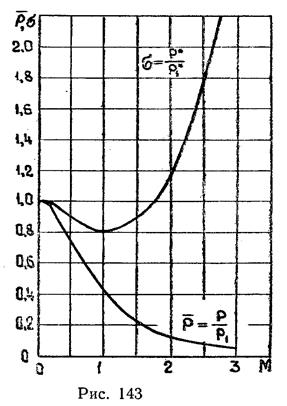
Статическое давление по длине теплового сопла уменьшается. Это связано с ростом скорости: для увеличения количества движения газа необходимо, чтобы вдоль потока действовала сила, а причиной ее появления в цилиндрической трубе может быть только разность давлений на входе и выходе. Давление торможения по длине сопла также изменяется. На дозвуковом участке оно падает, на сверхзвуковом — возрастает. Зависимость статического давления и давления торможения от числа М в произвольном сечении теплового сопла приМ₁=0,1 и k=1,4показана на рис. 143.

Падение давления торможения в результате подвода тепла называется тепловым сопротивлением. Рассмотрим тепловое сопротивление при малых скоростях движения газа в цилиндрической трубе с внешним подводом тепла. Для этого запишем разность давлений торможения на входе и выходе и определим ее знак. При малых числах М связь между полным и статическим давлением можно брать по уравнению Бернулли для несжимаемой жидкости

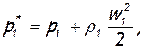
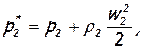
так как плотность очень слабо зависит от скорости. Однако нужно заметить, что считать плотность постоянной для всего потока от входа до выхода нельзя, потому что она сильно изменяется вследствие подвода тепла (в связи с этим в предыдущих формулах плотности на входе и выходе помечены разными индексами). Произведя вычитание

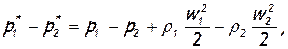
подставим вместо разности статических давлений ее выражение из уравнения количества движения (3.31)

p₁ – p₂ = ρ₂ w₂² – ρ ₁ w₁².

Тогда после небольших преобразований получим

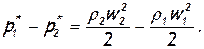(7.25)

Из формулы (7.25) видно, что если к газу подводится тепло, т.е. скорость его возрастает, то 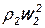> 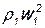, следовательно, p₂*<p₁*, значит, в этом случае существует тепловое сопротивление. При отводе тепла 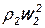< 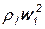,p₂*>p₁*, т.е. получается отрицательное тепловое сопротивление. Таким образом, в отличие от гидравлического, тепловое сопротивление может быть как положительным, так и отрицательным.

При больших скоростях газа тепловое сопротивление, а также изменение статического давления рассчитывается следующим образом. Уравнение количества движения в полных импульсах для массы газа, движущегося в цилиндрической трубе без трения, запишется, как

Ф₁ = Ф₂,

потому что между входным и выходным сечением на поток в направлении движения не действует никаких сил. Записав это с помощью газодинамических функций потока импульсаr(λ) и f(λ)

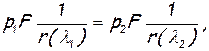
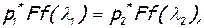
нетрудно получить формулы для расчета статического и полного давлений на выходе из трубы или в ее произвольном сечении

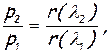(7.26)

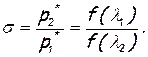(7.27)

Температуры газа в любом сечении трубы рассчитываются по известной зависимости

Т = Т* ,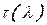

причем температура торможения должна быть задана. Обычно задают величину

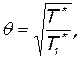(7.28)

называемую степенью повышения температуры.

Для расчета по этим формулам необходимо знать приведенную скорость в расчетном сечении. Она определяется следующим путем. Записав отношение приведенных скоростей в произвольном сечении и в сечении входа

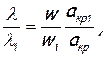
заменим в нем отношение скоростей с помощью уравнений неразрывности, состояния и формулы (7.26)

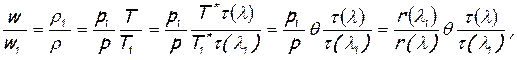
а отношение критических скоростей представим так:

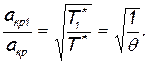
Тогда

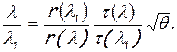
Используя формулы (2.59) и (3.39), преобразуем отношение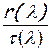

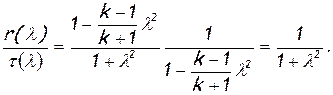
Подставив это в предыдущее равенство, получим

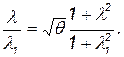(7.29)

Формула (7.29) представляет относительно λ квадратное уравнение. При его решении знак минус перед квадратным корнем относится к случаю дозвукового течения, а знак плюс — к случаю сверхзвукового. По уравнению (7.29) определяется λ в любом сечении цилиндрической трубы в зависимости от степени подогрева θ и λ на входе.

При определенных условиях течения газа по цилиндрической трубе с внешним подогревом наступает тепловой кризис. Тепловым кризисом называется такой режим течения, при котором скорость на выходе из трубы достигается критической. При тепловом кризисе невозможно:

1) увеличение расхода газа выше критического значения;

2) увеличение скорости газа на выходе;

3) увеличение подогрева газа при сохранении постоянной начальной скорости.

Таким образом, при тепловом кризисе λ₂=1, λ₁= λ_1кр, θ= θ_кр.

Заметим, что дозвуковая часть теплового сопла работает на режиме теплового кризиса, и увеличение скорости после критического сечения происходит лишь потому, что изменяется знак теплового воздействия: теплоподвод сменяется теплоотводом.

Если в уравнении (7.29) положитьλ₂=1, то оно принимает вид

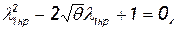
откуда легко получить

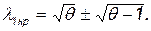(7.30)

По этой формуле определяется критическое значение приведенной скорости при входе в трубу, при котором наступает тепловой кризис. Для тех камер сгорания, которые работают с очень высокой степенью повышения температуры, с помощью такого проверочного расчета устанавливают, способна ли камера пропустить расчетное количество газа.

Отношение статических давлений и коэффициент восстановления давления при тепловом кризисе зависят от степени подогрева. С ее увеличением р₂/р_f и 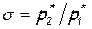уменьшаются, стремясь к определенному пределу. Так, например, при k=1,4 при .

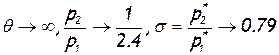В заключение нужно заметить, что в чистом виде тепловое сопло в технике не применяется, но в комбинации с геометрическим соплом встречается часто. Комбинация геометрического и теплового воздействия встречается, например, при догорании топлива в суживающейся части реактивных сопел, при охлаждении стенок сопел реактивных двигателей. С тепловым сопротивлением приходится встречаться при расчетах и исследованиях устройств, в которых газ движется с подводом или отводом тепла, — камер сгорания, воздухоподогревателей, воздухоохладителей и т.п.

Течение газа с подводом и отводом механической энергии

Подвод и отвод механической энергии оказывает воздействие на газовый поток. Это легко установить с помощью уравнения обращения воздействий (7.6), которое для случая только одного механического воздействия имеет вид:

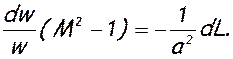(7.87)

Из этого уравнения следует, что в дозвуковом потоке (М<1) внешняя механическая работа, отданная газом (dL>0), вызывает рост скорости (dw>0), а подведенная к газу (dL<0) — падение скорости (dw<0). В сверхзвуковом потоке — наоборот: при dL>0 скорость уменьшается (dw<0), а при dL<0 — растет (dw>0).

В теории одномерных потоков[5] рассматривается так называемое «механическое сопло», состоящее из последовательно расположенных турбины (dL>0) и компрессора (dL<0), между которыми находится критическое сечение (М=1). Теоретически такаясистема способна преобразовать дозвуковой поток в сверхзвуковой, но практического значения она не имеет, ввиду трудности сохранения бесскачкового течения в сверхзвуковом компрессоре и сложности всего устройства. Тем не менее, общие выводы, вытекающие из уравнения (7.87), полезны при анализе условий перехода через скорость звука в межлопаточных каналах сверхзвуковых рабочих колес турбомашин.

Если сравнить механическое воздействие с тепловым, рассматривая формулу (7.6) и уравнение энергии (2.6), то можно обратить внимание на то, что в эти уравнения величины dL и dQ_е входят в различных сочетаниях (с разными коэффициентами и с разными знаками), поэтому их влияние на различные параметры потока не может быть одинаковым. Действительно, анализ показывает, что при подводе механической работы (dL<0) в дозвуковой области (М<1) параметры р, Т, ρ, р^*, Т^*, ρ^* — возрастают, а скорость уменьшается, тогда как при подводе тепла (dQ_е>0) Т^*— также возрастает, Т — имеет максимум при 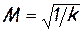но, р, ρ, р^*, ρ^* — уменьшаются, а скорость возрастает.

Передача механической энергии в газовый поток извне или отвод ее наружу связан с воздействием поля массовых сил на частицы движущейся жидкости. Этим полем может быть либо внешнее поле немеханического происхождения (например, электрическое или электромагнитное), либо поле инерционных сил, возникающее в сложном движении. Первый случай относится к движению заряженных частиц жидкости и составляет предмет изучения специальной отрасли гидродинамики — магнитной газодинамики [6]. Второй случай связан с движением обычной жидкости или газа в рабочих колесах турбомашин.

Расчет газовых потоков в каналах рабочих колес часто приходится вести в относительном движении. Подвод и отвод механической работы оказывает влияние на параметры относительного движения. Рассмотрим, в чем заключается это влияние.

Газ, движущийся в межлопаточном канале рабочего колеса, участвует в сложном движении. Он движется относительно лопаток со скоростью w и перемещается вместе с каналами колеса с переносной скоростью u. Следуя терминологии, принятой в теории турбомашин, будем обозначать абсолютную скорость через с, относительную — через w и переносную — через u. Тогда

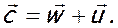(7.88)

На рис. 165 треугольников скоростей с, w и u изображен в абсолютной системе координат, неподвижно зафиксированной относительно корпуса машины. В ней оси r, u, а направлены соответственно по радиусу, по окружности колеса и по оси машины.

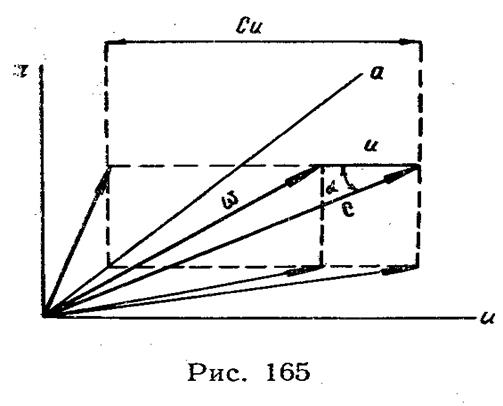
Применяя к этому треугольнику теорему косинусов, можно записать

w² = с² + и² – 2 c u соsα,

откуда

c² = w² — u² + 2 с_u u . (7.89)

так как с_°соsα=с_u.

Уравнение энергии в абсолютном движении запишем в форме (2.4), переменив обозначение скорости с w на с, а именно

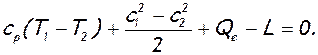(7.90)

Входящая в него внешняя механическая работа L может быть найдена следующим образом. По второй теореме Эйлера о моменте количества движения (3.45) момент внешних сил, действующих на струю, равен

m = m_сек ( r₂ с_2u – r₁ с_1u ).

Представив работу L, совершенную единицей массы газа, как мощность, приходящуюся на единицу массового расхода, нетрудно получить[7]

L = – m_°ω/ m_сек = – ω( r₂ с_2u – r₁ с_1u ).

Так как ωr=u, то

L = с_1u u₁ – с_2u u₂. (7.91)

После подстановки значений абсолютной скорости с, найденных из зависимости (7.89), и работы L, найденной из формулы (7.91), в уравнение энергии (7.90), последнее приобретает вид:

с_p(t₁ – t₂ ) + (w₁² – u₁²)/2 – (w ₂² – u₂²)/2 + q_e = 0. (7.92)