Преобразование звезды в эквивалентный треугольник

При переходе от звезды к треугольнику известными являются сопротивления R₁, R₂, R₃ лучей звезды. Значения сопротивлений треугольника определяются в результате совместного решения уравнений (25):

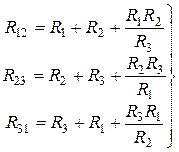(26)

Сопротивление стороны треугольника равно сумме сопротивлений прилегающих лучей звезды и произведения их, деленного на сопротивление третьего луча.

Пример.

Дано: U_AB=U_BC=220(B), r₀=0,5 Ом;

r₁=r₂=r₇=1Ом, r₃=r₄=4 Ом;

r₅=8 Ом, r₆=r₈=2 Ом.

Преобразовав схему, определить токи I_A, I_B, I_C.

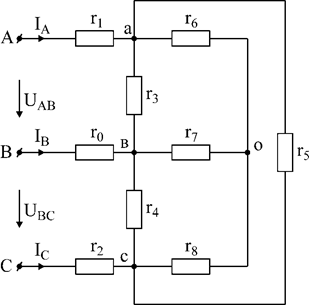
Рис.1

Решение: Сопротивления r₆, r₇, r₈ образуют звезду;

сопротивления r₃, r₄, r₅ образуют треугольник.

Преобразуем звезду сопротивлений r₆, r₇, r₈ в треугольник r₉-r₁₀-r₁₁:

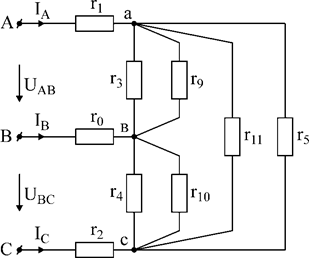
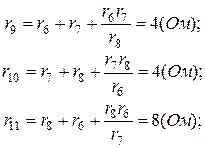
Рис.2

В результате преобразования получили два треугольника, параллельных друг другу (рис.2). Найдем эквивалентные сопротивления сторон треугольника (рис.3):

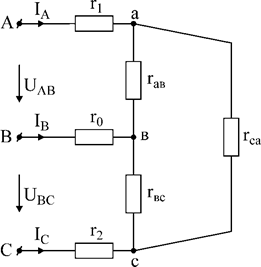
Рис.3

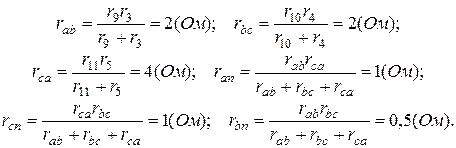
Полученный треугольник преобразуем в звезду (рис.4)

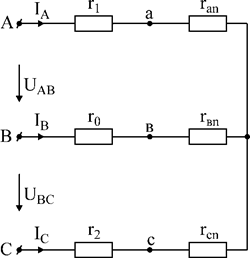
Рис.4

Т.к. сопротивления r₁; r₀; r₂ не подвергались преобразованиям, то через них протекают искомые токи I_A; B_C; I_C. Для их нахождения составим систему уравнений по законам Кирхгофа:

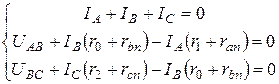
В результате решения системы получим:

I_A= 110 (A); I_B= 0; I_C= -110 (A).

Примечание:

1. Преобразование источника напряжения, обладающего внутренним сопротивлением, в эквивалентный источник тока с внутренней проводимостью было рассмотрено ранее. Необходимость замены одного вида источника другим часто возникает при решении задач. При этом следует помнить:

Под эквивалентностью источников понимают неизменность токов, напряжений и мощностей во внешней электрической цепи, присоединенной к источникам.

Мощности, расходуемые во внутренних сопротивлениях источника тока и источника напряжения, не одинаковы.

2. Преобразование активного треугольника в активную звезду и наоборот, рассмотрено в приложении I.

Контрольные вопросы.

1. Записать формулы эквивалентного сопротивления ветви при последовательном соединении её элементов и эквивалентной проводимости участка цепи при параллельном соединении ветвей на данном участке.

2. Что такое смешанное соединение элементов? Какой порядок эквивалентирования сопротивлений при таком соединении.

3. Записать формулы перехода от треугольника к эквивалентной звезде и наоборот.

Методы расчета сложных электрических цепей

Цель лекции № 4.

Ознакомившись с данной лекцией студент должен знать:

1. Суть каждого из ниже рассмотренных методов.

2. Уметь применять данные методы при решении задач.