Нелинейная регрессия и ее классификация
Во многих практических случаях моделирование экономических зависимостей линейными уравнениями дает вполне удовлетворительный результат и может использоваться для анализа и прогнозирования. Однако в силу многообразия и сложности экономических процессов ограничиться рассмотрением лишь линейных регрессионных моделей невозможно. Многие экономические зависимости не являются линейными по своей сути, и поэтому их моделирование линейными функциями, безусловно, не даст положительного результата. Так, например, нелинейными являются производственные функции (зависимости между объемом произведенной продукции и основными факторами производства - трудом, капиталом и т.п.), функции спроса (зависимость между спросом на товары или услуги и их ценами или доходом) и др.
Различают два класса нелинейных регрессий:
1) регрессии, нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам. К таким функциям относятся квазилинейные функции.
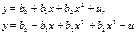 |
Например, это полиномы различных степеней
Равносторонняя гипербола
2)
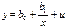 |
регрессии нелинейные по оцениваемым параметрам. К таким регрессиям относятся нелинейные функции второго класса.
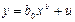 |
Например, степенная функция
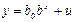 |
Показательная
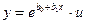 |
Экспоненциальная
Нелинейная регрессия по включенным переменным не таит каких-либо сложностей в оценке ее параметров. Она определяется, как и в линейной регрессии, методом наименьших квадратов, так как эти функции линейны по параметрам. Так, например, в полиноме второй степени
заменив х = х1, х2 = х2, получим у = b0 + b1x1 + b2x2 + u. Применив метод наименьших квадратов для оценки коэффициентов этого полинома, получим следующую систему нормальных уравнений
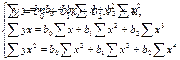 |
Ее решение возможно методом Крамера.
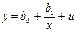 |
Среди класса нелинейных функций, параметры которых легко оцениваются с помощью МНК, следует назвать хорошо известную в эконометрике равностороннюю гиперболу:
Она может быть использована для характеристики связи удельных расходов сырья, материалов, топлива с объемом выпускаемой продукции, времени обращения товаров от величины товарооборота. Классическим ее примером является кривая Филлипса, характеризующая нелинейное соотношение между нормой безработицы х и процентом прироста заработной платы у. Английский экономист А.В.Филлипс, анализируя данные более чем за 100-летний период, в конце 50-х годов 20 века, установил обратную зависимость прироста заработной платы от уровня безработицы.
Заменив в уравнении равносторонней гиперболы 1/х на z, получим уравнение линейной регрессии y = b0 + b1 z + u, оценка параметров которого может быть дана с помощью МНК.
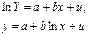 |
Модели вида
называются полулогарифмическими моделями. Эти модели также относятся к нелинейным моделям относительно включенных в анализ объясняющих переменных, но линейным по параметрам.
Такие модели обычно используются в тех случаях, когда необходимо определять темп роста или прироста каких-либо экономических показателей. Например, при анализе банковского вклада по первоначальному вкладу и процентной ставке, при исследовании зависимости прироста объема выпуска от относительного (процентного) увеличения затрат ресурса, бюджетного дефицита от темпа роста ВНП, темпа роста инфляции от объема денежной массы и т.д.
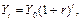 |
Зависимость
где Y0 – начальная величина переменной Y (например, первоначальный вклад в банке); r – сложный темп прироста величины Y (процентная ставка); Yt – значение величины Y в момент времени t (вклад в банке в момент времени t). Эта модель легко сводится к полулогарифмической первого вида, параметры которой легко оцениваются с помощью МНК.
Иначе обстоит дело с регрессией, нелинейной по оцениваемым параметрам. Данный класс нелинейных моделей подразделяется на два типа: нелинейные модели внутренне линейные и нелинейные модели внутренне нелинейные.
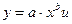 |
Если нелинейная модель внутренне линейна, то она с помощью соответствующих преобразований может быть приведена к линейному виду. Например в экономических исследованиях при изучении эластичности спроса от цен широко используется степенная функция
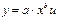 |
где y – спрашиваемое количество
х – цена
u – случайная ошибка.
Данная модель нелинейна относительно оцениваемых параметров, так как включает параметры а и b неаддитивно. Однако ее можно считать внутренне линейной, так как логарифмирование данного уравнения, например, по основанию e приводит его к виду
Оценка параметров в полученном уравнении может быть произведена с помощью МНК.
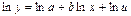 |
Наибольшее распространение степенной функции в эконометрике связано с тем, что параметр b имеет четкое экономическое истолкование, – он является коэффициентом эластичности. Это значит, что коэффициент b показывает, на сколько % в среднем результат, если фактор изменится на 1%.
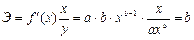 |
Для степенной функции коэффициент эластичности будет рассчитываться следующим образом
При b<0 характеризуется эластичность спроса, а при b>0 – предложения.
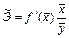 |
В других функциях коэффициент эластичности зависит от значений фактора x. В силу этого для них обычно рассчитывается средний показатель эластичности

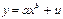 |
Если же модель степенной регрессии представить в виде
то она становится внутренне нелинейной, так как ее невозможно превратить в линейный вид. В этом случае, то есть, если модель внутренне нелинейна по параметрам, используются итеративные процедуры, успешность которых зависит от вида уравнений и особенностей применяемого итеративного подхода. Модели внутренне нелинейные по параметрам могут иметь место в эконометрических исследованиях, однако гораздо большее распространение получили модели, приводимые к линейному виду.
Рассмотренные функции регрессий легко обобщаются на большее количество переменных.Ввиду четкой интерпритации параметров наиболее широко используется степенная функция. В степенной функции
Коэффициенты bj являются коэффициентами эластичности.
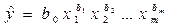 |
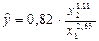 |
Например, при исследовании спроса на мясо получено уравнение
где у – количество спрашиваемого мяса, х1 – цена, х2 – доход.
Рост цен на 1% при том же доходе вызывает снижение спроса в среднем на 2,63%. Увеличение дохода на 1% обусловливает при неизменных ценах рост спроса на 1,11%.
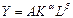 |
Зачастую данная степенная модель используется при анализе производительных функций. Например, хорошо известна производственная функция Кобба-Дугласа
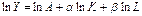 |
После логарифмирования обеих частей получим
Здесь α и β – эластичности выпуска по затратам капитала и труда соответственно. Сумма этих коэффициентов является таким важным экономическим показателем, как отдача от масштаба. При α + β = 1 говорят о постоянной отдаче от масштаба (во сколько раз увеличиваются затраты ресурсов, во столько же раз увеличивается выпуск). При α + β <1 имеет место убывающая отдача от масштаба (увеличение объема выпуска меньше увеличения затрат ресурсов). При α + β >1 – возрастающая отдача от масштаба (увеличение объема выпуска больше увеличения затрат ресурсов).
Варианты сведения нелинейной регрессии к линейной.
