Способ эксцентрических секущих сфер

Способ эксцентрических секущих сфер применяется, когда одна из осей -

проецирующая прямая, вторая линия уровня.

Пример. Построить линию пересечения поверхности конуса вращения Ф и

поверхности тора Ф', имеющих общую фронтальную плоскость симметрии. Оси i и i′ не пересекаются (рисунок 6.5). Опорные точки линии пересечения (высшая 1, низшая 6) определяются пересечением главных меридианов на плоскости П_2. Для определения случайных точек, принадлежащих линии пересечения тора с конусом, можно применить вспомогательные секущие сферы, центры которых будут расположены на оси конуса. Сферы необходимо подбирать так, чтобы они пересекали тор по окружностям.

Для определения центра и радиуса вспомогательной секущей сферы проведем произвольную плоскость Σ (Σ₂), проходящую через ось тора (т.e. Σ ┴П₂). Плоскость Σ пересечет тор по окружности радиуса L₂,C₂ с центром в точке С₂. Через центр С₂ проведем прямую перпендикулярную Σ и пересекающую ось конуса в точке О₂, т.е. линия С₂О₂ (касательная к осевой окружности тора). Точка О₂ есть центр вспомогательной секущей сферы, а прямая O₂L₂ - радиус этой сферы R. Определим линии пересечения вспомогательной секущей сферы с конусом и тором. С конусом сфера пересекается по окружности, диаметр которой А₂В₂. С тором сфера пересекается по окружности, диаметр которой L₂N₂ .

А₂В₂ ∩L₂N₂ = 2₂. Точка 2₂ одна из точек искомой линии пересечения. Аналогично построены точки 5₂, 3₂, 4₂, 6₂.

Для построения горизонтальных проекций точек линии пересечения используем параллели тора, как показано на рисунке 6.5, для точек 5₁ и 6₁. Так как точки 1 и 6 принадлежат меридианам поверхностей, на П₁ они проецируются на горизонтальную ось тора и конуса, которые совпадают.

Полученные точки соединяем с учетом видимости плавной кривой линией. На плоскости П₁ видимость линии пересечения определяет плоскость Г (Г₂). Часть линии 2₁, 1₁, 2'₁, - видима. Часть линии 3₁, 4₁, 5₁, 6₁, 5'1, 4'₁, 3'₁, - невидима. На плоскости П₂ видимость определяет плоскость Т (Т₁). Относительно этой плоскости линия пересечения - симметричная линия. Видимая часть линии 6₂, 5'₂, 4'₂, 3'₂, 2₂, 1'₂, совпадает с невидимой ее частью 6₂, 5₂, 4₂, 3₂, 2₂, 1₂. На чертеже изображаем видимую часть линии пересечения сплошной основной линией

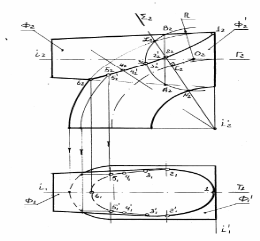
Рисунок 6.5

Указания к выполнению работы

Лист формата А3 (расположение альбомное) условно разделяем на две части. В левой части листа выполняем задачу 6.1, а в правой 6.2. Способ нахождения линии пересечения выбираем в зависимости от того, какие тела пересекаются. В нашем примере задача 6.1 выполнена способом концентрических сфер, смотри пример на рисунке 6.4 в разделе 6.2.2. Задача 6.2 выполнена способом эксцентрических сфер. Пример решения такой задачи приведен на рисунке 6.5 в том же разделе пособия.

Контрольные вопросы

6.4.1 Назвать общий алгоритм пересечения поверхностей.

6.4.2 Назовите способы определения линии пересечения поверхностей.
6.4.3 Охарактеризуйте характерные точки линии пересечения.

6.4.4 Какая линия получается при пересечении многогранных поверхностей.

6.4.5 В каком случае пересечения поверхностей применяется метод концентрических сфер.

6.4.6 В каком случае пересечения поверхностей применяется метод эксцентрических сфер.

6.4.7 По каким линиям пересекаются между собой поверхности вращения, имеющие общую ось (соосные поверхности).

7 Расчетно-графическая работа по теме «Аксонометрические проекции»

Цель работы научиться выполнять аксонометрические проекции по комплексному чертежу.

7.1 Задание: выполнить аксонометрическую проекцию тела с выемкой или группы пересекающихся тел. Данные для работы взять с РГР5 или РГР 6.

7.2 Теоретический раздел.

Аксонометрические проекции применяются в качестве вспомогательных проекций к комплексному чертежу, когда требуется поясняющее наглядное изображение формы детали или предмета.

Сущность метода аксонометрии заключается в следующем: объект относят к прямоугольной декартовой системе координат и проецируют его вместе с осями координат пучком параллельных лучей на некоторую плоскость проекций, называемую аксонометрической. (Смотри рисунок 7.1) Полученное на ней изображение называют аксонометрическим (или просто аксонометрия), а проекции координат осей – аксонометрическими осями координат. Слово «аксонометрия» - греческое, состоит из двух слов axon – ось, metreo – измеряю, что в переводе означает «измерение по осям».

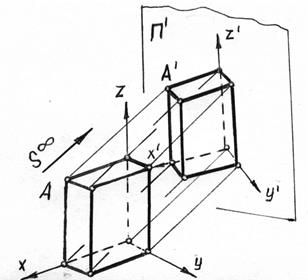
Рисунок 7.1

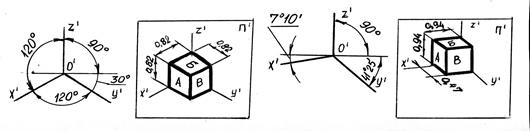
В зависимости от направления проецирующих лучей и искажения линейных размеров вдоль осей аксонометрические проекции делятся на прямоугольные и косоугольные. Прямоугольные аксонометрические проекции дают более наглядное изображение и поэтому чаще применяются в машиностроении. На рисунке 7.2 дано наименование видов аксонометрических проекций, расположение осей и показатели искажения линейных размеров по осям в соответствии с ГОСТ 2.317.

Прямоугольные проекции

изометрическая диметрическая

Косоугольные проекции

фронтальная изометрическая горизонтальная изометрическая

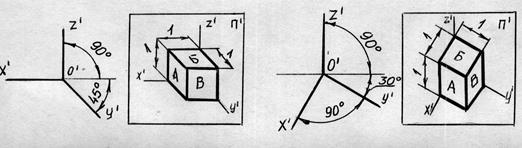
фронтальная диметрическая

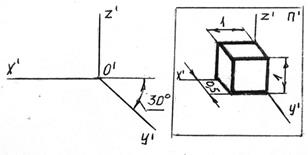
Рисунок 7.2

Показателем искажения называется отношение длин звеньев на аксонометрической проекции к соответствующей натуральной величине звена и они в соответствии с осями обозначаются U;V;W, если U=V=W , то этот вид аксонометрии называется изометрия; если U=2V=W или 2U=V=W, то это - диметрия и если U≠V ≠W≠U, то это - триметрия.

Следует обратить внимание на то, что в техническом черчении для упрощения построений искажение по осям не учитывается, а размеры по осям в изометрии выполняются в натуральную величину, а в диметрии с соотношением 1:0,5:1, то есть само изображение в изометрии увеличивается в 1,22 раза, а диметрии в 1,06 раз, однако наглядность при этом никак не изменяется.

7.2.1 Аксонометрическая проекция точки и прямой

Известно, что все поверхности предметов состоят из линий, а линии из точек, поэтому рассмотрим построение аксонометрической проекции точки на рисунке 7.3. Точка А задана своими координатами X,Y и Z.

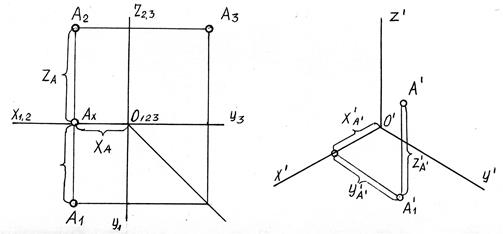
Рисунок 7.3

Аксонометрическая проекция отрезка может быть легко построена по двум точкам (концам этого отрезка).

7.2.2 Аксонометрические проекции плоских фигур и геометрических тел

На примере, изображенном на рисунке 7.4 рассмотрим построение плоской фигуры на трех плоскостях проекций. Для упрощения построений считаем, что фигура расположена в плоскостях П₁, П₂, и П₃ .

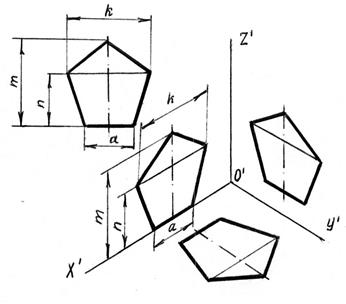
Рисунок 7.4

На примере, изображенном на рисунке 7.5, рассмотрим построение прямоугольной изометрической проекции призмы на трех плоскостях проекций. Если основанием призмы является правильный многоугольник, например шестиугольник, то построение вершин основания по координатам можно упростить, проведя одну из осей через центр основания. Построив изометрию основания призмы, из вершин его основания проводим прямые, параллельные соответствующим осям ; ; 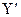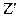(в зависимости от того, как расположена призма) и на этих прямых от вершин откладываем высоту призмы, тем самым получая изометрию шести точек вершин другого основания. Дальнейшее построение сводится к тому, что отделяем видимые линии от невидимых и наводим полученное изображение.

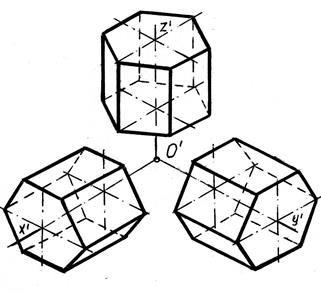
Рисунок 7.5

На рисунке 7.6 показано выполнение изометрии правильной шестигранной пирамиды, заданной высоты. Рисуем изометрические оси, причем начало их помещаем в центр шестигранника и выполняем изометрию нижнего основания. Дальше от центра 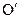откладываем вверх высоту пирамиды и отмечаем точку 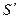, соединяем ее с вершинами нижнего основания. Сплошной толстой линией обводим видимый контур, линии невидимого контура изображаем штриховой.

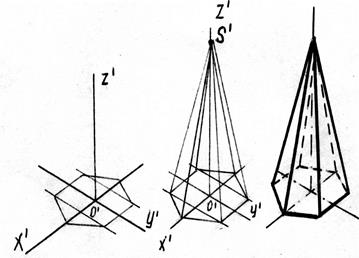
Рисунок 7.6

В такой же последовательности выполняются аксонометрические проекции цилиндров и конусов (смотри рисунок 7.7). При этом приходится рисовать эллипсы, в виде которых обычно проецируются окружности.

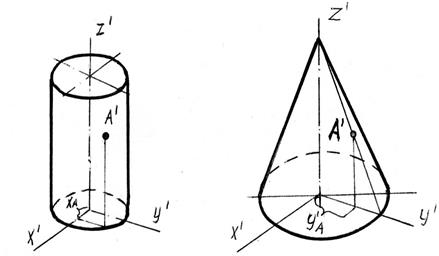
Рисунок 7.7–Изометрия цилиндра и конуса с точкой А на поверхности.

7.2.3 Прямоугольная изометрическая проекция окружности

Если построить изометрическую проекцию куба (сторона равна D), в грани которого вписаны окружности диаметра D, то квадратные грани куба будут изображаться в виде ромбов, а окружности в виде эллипсов (смотри рисунок 7.8). Следует запомнить, что малая ось каждого эллипса всегда должна быть перпендикулярна большой оси. Большие оси всех трех эллипсов направлены по большим диагоналям ромбов. При построении изометрической проекции окружности без сокращений по осям U=V=W=1 длина большой оси эллипса берется 1,22 D, а малой 0,71 D.

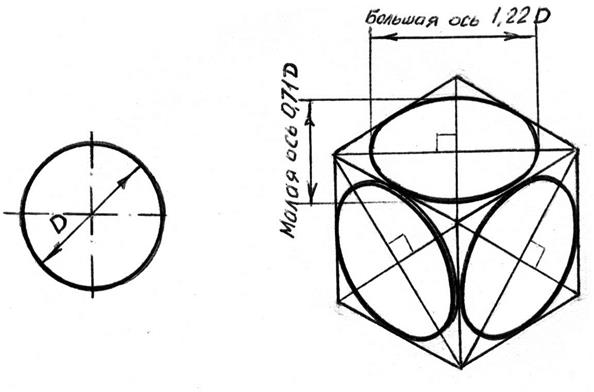
Рисунок 7.8

Примечание: вместо эллипсов, рекомендуется применять овалы, очерченные дугами окружностей (рисунок 7.9).

7.2.4 Изометрия шара (рисунок 7.10)

Изометрия шара выполняется следующим образом: из намеченного центра проводим окружность , диаметр которой равен 1,22 D (D диаметр шара) – это будет изображение шара в изометрии. Если необходимо построить половину, четверть или три четверти шара, то необходимо сначала вычертить один, два или три овала и тогда овалы и точки K;M;L определяют границы трех четвертей шара. На что следует обратить внимание при штриховке, что линии штриховки сечений наносят параллельно одной их диагоналей проекций квадратов, лежащих в соответствующих координатных плоскостях, стороны которого параллельны аксонометрическим осям.

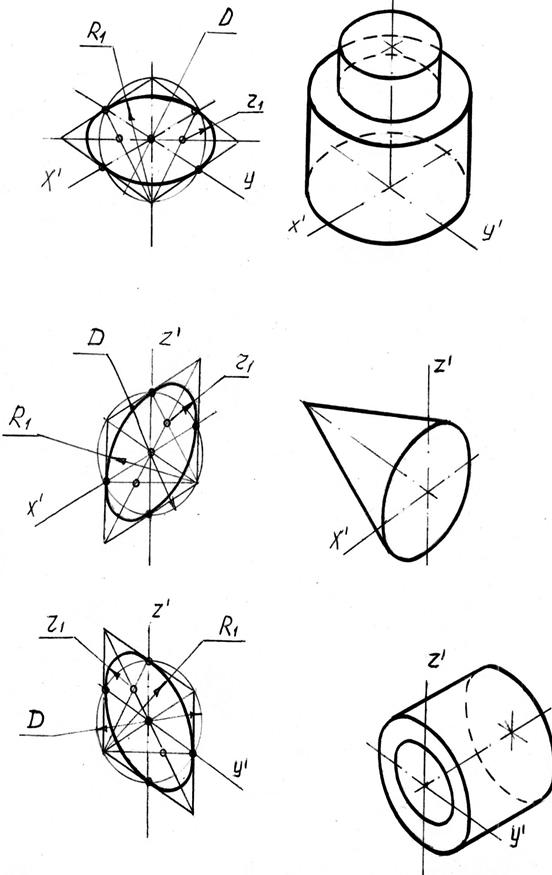
Рисунок 7.9

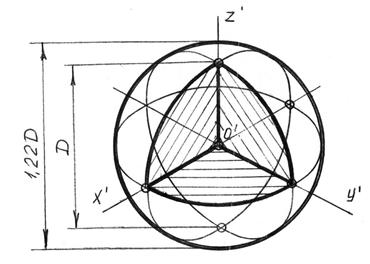
Рисунок 1.10