Ньютоннның интерполяциялық формулалары

Егер интерполяциялық түйіндердің бір бірінен ара қашықтығы тұрақты болса, практикада Ньютонның интерполяциялық формулалары қолданылады. Бұл формулалар екіге бөлінеді:

1 Алдыға қарай интерполяциялау;

2 Кері интерполяциялау;

Егер берілген х нүктесінің мәні кестенің бас жағында жатса, 1-формуласы қолданылады:

(4.11)

.

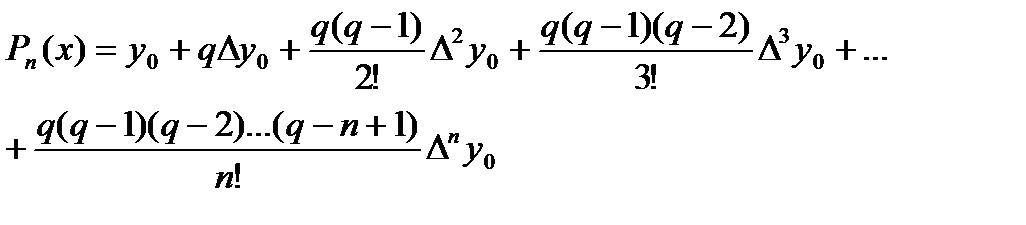Мұндағы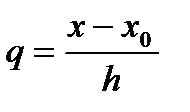

Егер берілген х нүктесінің мәні кестенің соңғы жағянда жатса, 2-формула қолданылады:

(4.12)

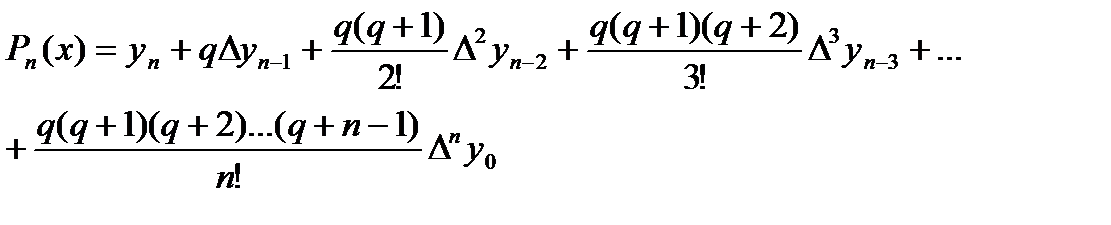
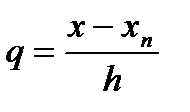
Формулалардағы 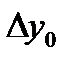, , 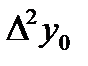т.с. сияқтылар шектік айырымдар деп аталады және 7-кестені толтыру арқылы анықталады. Кестедегі мысал үшін 6 интерполяциялық түйін және шектік айырымдардың 4-ші дәрежесіне дейінгі мәндер қарастырылған. 1-формула үшін кестенің бірінші жолындағы мәндер, 2-формула үшін кестенің соңғы жолындағы мәндер қолданылады.

7-кесте – Шектік айырымдар кестесі

x	Y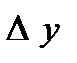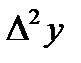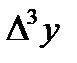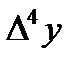
X0	Y0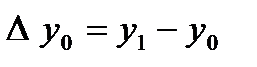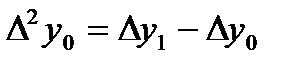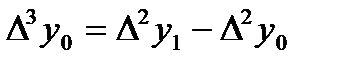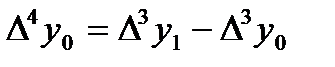
X1	Y1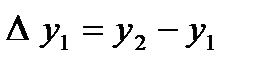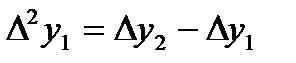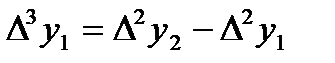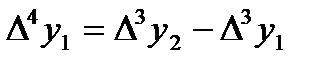
X2	Y2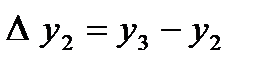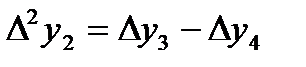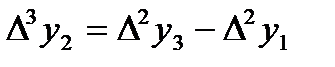
X3	Y3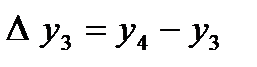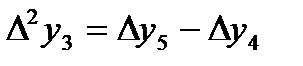
X4	Y4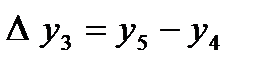
X5	Y5

Егер интерполяциялық түйіндер саны 1 немесе 2-ге тең болса сызықты интерполяциялық формуланы қолдануға болады: .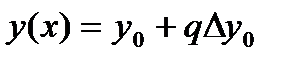

Қателіктерін бағалау:

1-формула үшін мына формула қолданылады:

,

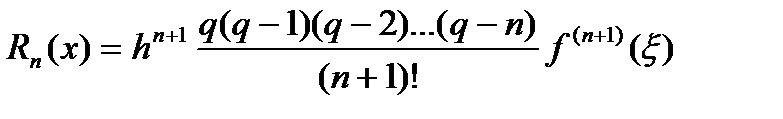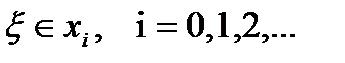
немесе

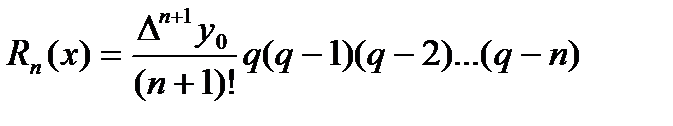
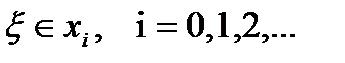
2-формула үшін мына формула қолданылады:

,

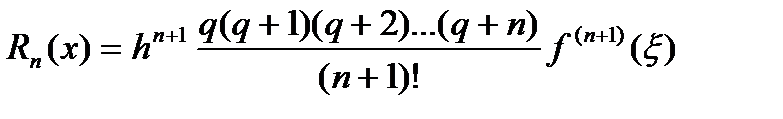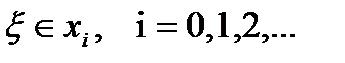
Мысал:

y=lg(x) функциясының мәндері 8-кестеде берілген, lg1001 мәнін табу керек.

3-ретті шектік айырымдар тұрақты бола бастағандықтан кестені толтыруды тоқтатамыз. Формулада n=3 деп аламыз. Q=0,1. x=1001. Ньютонның бірінші формуласын қолданамыз, себебі х-тің мәні кестенің бас жағында жатыр, сонда lg1001=3.00043417+0.5*10^-9 болатынын қалдық мүшенің формуласын қолдану арқылы анықтаймыз.

8-кесте – y=lg(x) функциясының мәндері және

шектік айырымдары кестесі

X	Y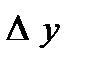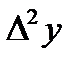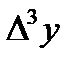
	3.0000000	43 214	-426
	3.0043214	42 788	-418
	3.0086002	42 370	-409
	3.0128372	41 961	-401
	3.0170333	41 560
	3.0211893

Лагранждың интерполяциялық көпмүшелігі

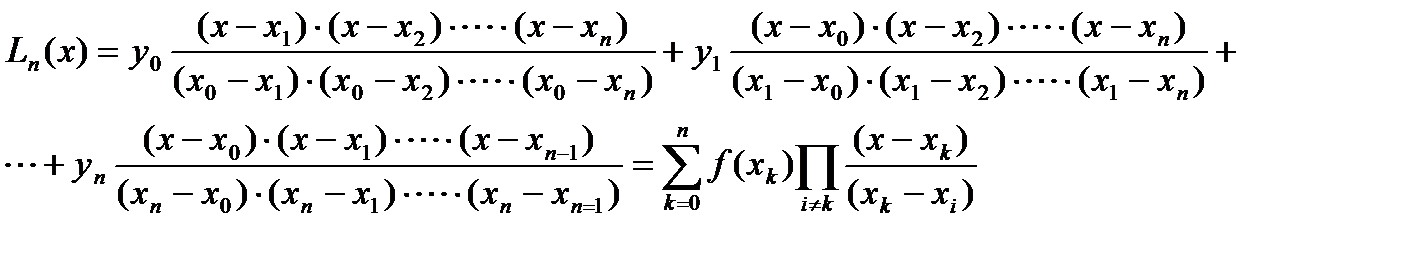(4.4)

Кей жағдайда есептеу процесін жеңілдету үшін x=at+b, x_j=at_j+b j=0,1,…,n сызықты алмастыруын жасау арқылы Лагранж коэффициенттерінің инварианттылығын қолдануға болады, онда (4.4)-формула келесі түрге келеді:

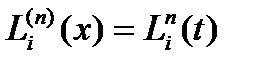(4.5)

Эйткен схемасы

Егер Лагранж көпмүшелігінің жалпы өрнегін анықтамай, тек белгілі бір нүктедегі функция мәнін есептеу керек болса, онда Эйткен схемасын қолдануға болады:

(4.6)

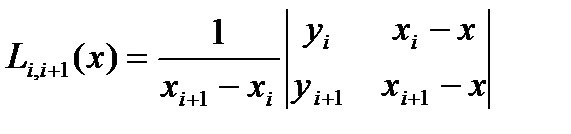
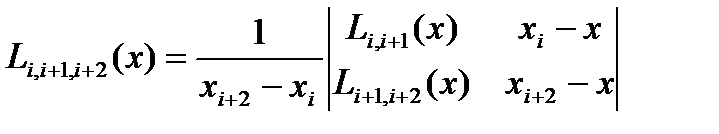
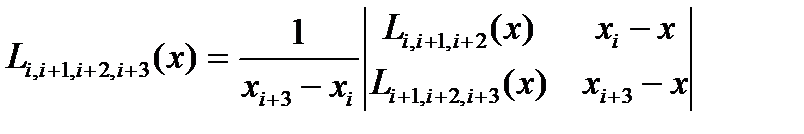т.с.с.

Эйткен схемасы келесі 6-кестені толтыру арқылы орындалады.

6-кесте – Эйткен схемасының толтырылу кестесі

xi	yi	Xi-x	Li-1,i	Li-2,i-1,i	Li-3,i-2,i-1,i	…
X0	Y0	X0-x
X1	Y1	X1-x	L01(x)
X2	Y2	X2-x	L12(x)	L012(x)
X3	Y3	X3-x	L23(x)	L123(x)	L0123(x)	…
X4	Y4	X4-x	L34(x)	L234(x)	L1234(x)	…

Эйткен схемасын есептеуді көршілес L_0123…n(x), L_0123…n,n+1(x) мәндері берілген дәлдік маңайында бір бірімен беттессе тоқтатуға болады.

X_i нүктелерінде y_i мәндерін қабылдайтын n-ші дәрежелі интерполяциялық көпмүшелік келсі түрде де жазылады:

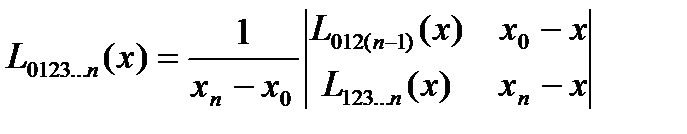. (4.7)

1-Мысал:

Төмендегі кестемен берілген функция үшін Лагранж көпмүшелігін құру.

I				(4.8) 3
xi		0.1	0.3	0.5
yi	-0.5		0.2

Шешімі: (4.4)-формула бойынша n=3, i=0,1,2,3 болғандағы өрнекті анықтаймыз:

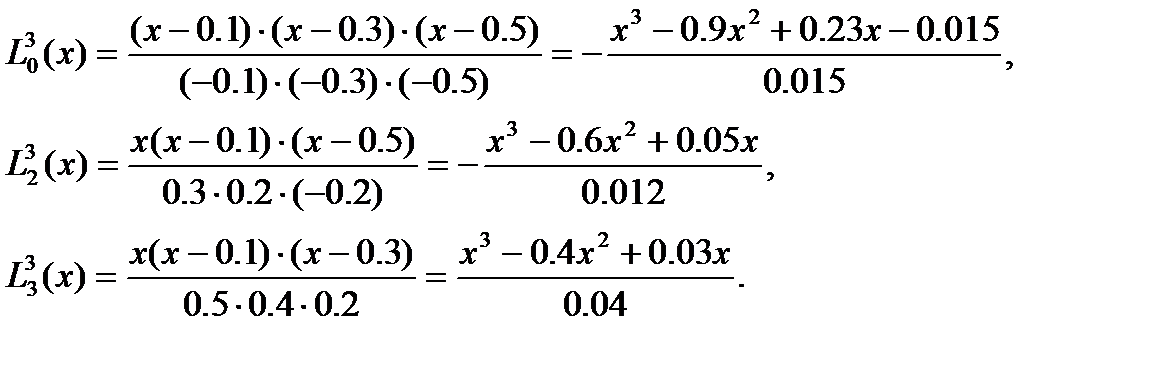
L₁³(x) мүшесін есептемейміз, себебі y₁=0. Бәрін бір біріне қосамыз да көпмүшеліктің соңғы түрін аламыз:

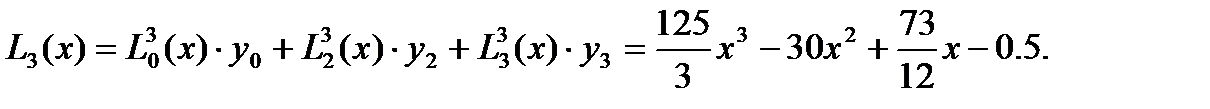
2-мысал:

Төмендегі кестемен берілген функцияның x=0.45 нүктесіндегі мәнін анықтау керек.

X	0.05	0.15	0.20	0.25	0.35	0.40	0.50	(4.9) 0.55
y	0.9512	0.8607	0.8187	0.7788	0.7047	0.6703	0.6065	0.5769

Шешімі:

Есептеуді жеңілдету үшін x=0.05t деп алайық. X-тердің мәні белгілі болғанда t-лардың мәндерін тауып алуға болады, олар: 1, 3, 4, 5, 7, 8, 10, 11. Және x=0.45 болғандағы t=9 болады. Есептеу қадамдары 6^’-кестеде келтірілген.

6^’-кесте – (4.9)-есептің есептелу қадамдары

I	ti-tj (i<>j)	Di	yi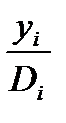
		-2	-3	-4	-6	-7	-8	-10	-725 760	0.9512	-0.0131*10-4
			-1	-2	-4	-5	-7	-8	26 880	0.8607	0.3202*10-4
				-1	-3	-4	-6	-7	-7 560	0.8187	-1.0829*10-4
					-2	-3	-5	-6	5 760	0.7788	1.3520*10-4
						-1	-3	-4	-3 456	0.7047	-2.0390*10-4
							-2	-3	2 520	0.6703	2.6599*10-4
							-1	-1	11 340	0.6065	0.5348*10-4
								-2	-80 640	0.5769	-0.0715*10-4

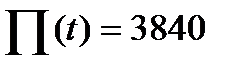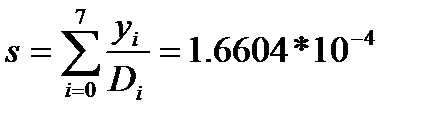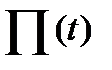
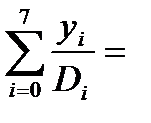
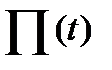
Сонымен y(0.45)= 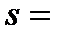3840*1.6604*10^-4=0.6376.