Пример определения реактивных усилий балки на двух шарнирных опорах с вертикальной нагрузкой

Задача

Определить реакции опор данной балки:

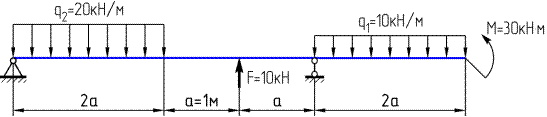
Решение

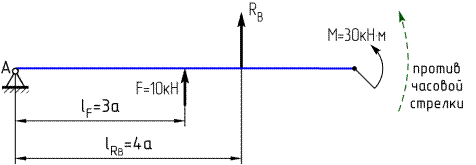
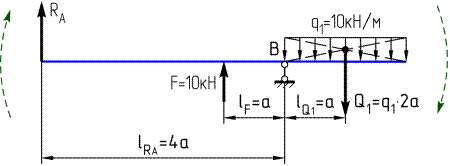
1. Обозначим опорные точки балки буквами А и В и изобразим в них реактивные усилия, возникающие от действия приложенной нагрузки:

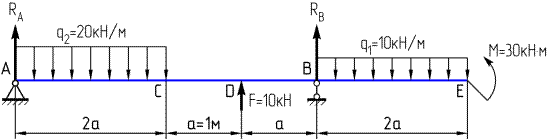
Так как все внешние силы, действующие на балку вертикальные (образуют параллельную систему сил), то и в шарнирно-неподвижной опоре А и в шарнирно-подвижной опоре В возникают только вертикальные реактивные силы R_A и R_B.

2. Наиболее рациональной формой двух уравнений равновесия для данной балки с вертикальной нагрузкой является вторая форма (2'):

,

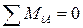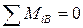
3. Составим первое моментное уравнение равновесия для нашей балки относительно опорной точки А: 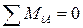. Это уравнение означает, что алгебраическая сумма моментов, возникающих в точке А от действия всех активных (заданных) и реактивных усилий, должна равняться нулю. Это утверждение можно перефразировать несколько иначе: сумма моментов, поворачивающих балку относительно точки А по часовой стрелки, должна равняться сумме моментов, поворачивающих её относительно этой точки против часовой стрелки. Визуально это легко представить, если мысленно открепить балку от опоры В, тогда она будет представлять собой рычаг с центром в точке А, который поворачивается действующими усилиями либо против либо по часовой стрелке.

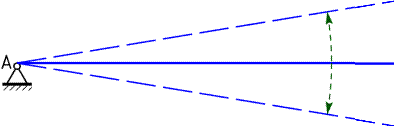
По часовой стрелке относительно точки А поворачивают балку распределенные силы q₁ и q₂:

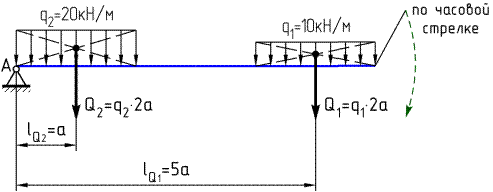
Найдем моменты этих сил относительно точки А, применяя правило №3 (см. выше):

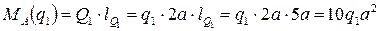
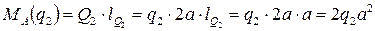
Против часовой стрелки относительно точки А поворачивают балку следующие усилия: сосредоточенный момент М, реактивная сила R_B и сосредоточенная сила F.

Найдем моменты этих усилий относительно точки А, применяя правила №1 и №2 (см. выше):

,

,

.

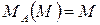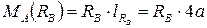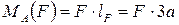Реакция R_A относительно точки А момента не создает, потому что её линия действия проходит через эту точку и, соответственно, плечо её относительно точки А равно нулю:

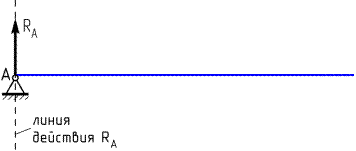
Приравняем сумму моментов, поворачивающих балку относительно точки А по часовой стрелке, к сумме моментов, поворачивающих её относительно этой точки против часовой стрелки:

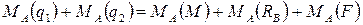
Подставив сюда найденные значения данных моментов, приходим к уравнению относительно неизвестной реакции R_B:

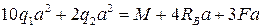
Выразим из этого уравнения реакцию R_B и найдем её численное значение, подставив известные значения внешних усилий и параметра а:

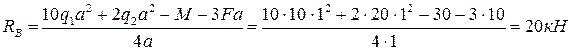
Значение реакции R_B получилось положительное, значит мы угадали истинное её направление. Если знак реактивного усилия получается отрицательным, то его первоначально выбранное направление нужно изменить на противоположное.

4. Поступая аналогично, составим второе моментное уравнение равновесия: 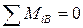, и найдем из него вторую реактивную силу R_A.

Мысленно открепив балку теперь от опоры А, получим рычаг с центром в точке В:

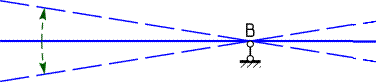
По часовой стрелке относительно точки В поворачивают балку следующие усилия: распределенная нагрузка q₁, сосредоточенная сила F и реактивная сила R_A.

Найдем моменты этих сил относительно точки В, применяя правила №2 и №3 (см. выше):

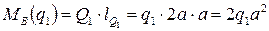
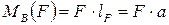
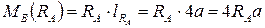
Против часовой стрелки относительно точки В поворачивают балку следующие усилия: распределенная нагрузка q₂ и сосредоточенный момент М.

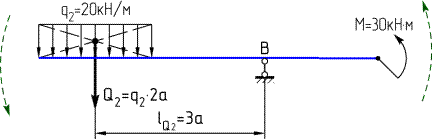
Найдем моменты этих усилий относительно точки В, применяя правила №1 и №3 (см. выше):

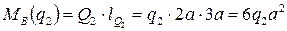
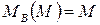
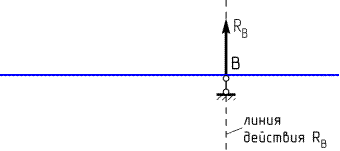
Реакция R_В относительно точки В момента не создает, потому что её линия действия проходит через точку В и, соответственно, плечо её относительно точки В равно нулю:

Приравняем сумму моментов, поворачивающих балку относительно точки В по часовой стрелке, к сумме моментов, поворачивающих её относительно этой точки против часовой стрелки:

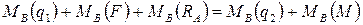
Подставив сюда найденные значения данных моментов, приходим к уравнению относительно неизвестной реакции R_А:

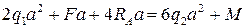
Выразим из этого уравнения реакцию R_А и найдем её численное значение, подставив известные значения внешних усилий и параметра а:

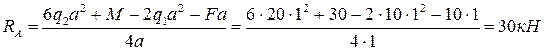
Значение реакции R_А также получилось положительное, значит мы угадали и её истинное направление.

5. Проверим правильность найденных значений реактивных усилий силовым уравнением равновесия в проекции на вертикальную ось Y: 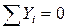. Если реакции найдены верно, то уравнение должно удовлетворяться тождественно. То есть, алгебраическая сумма всех активных и реактивных сил, действующих на балку, должна равняться нулю. Распределенная нагрузка в силовом уравнении равновесия представляется своей равнодействующей. В нашем случае: 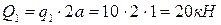и 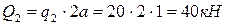. Силы, направленные вверх: R_A, F и R_B. Силы, направленные вниз: Q₁ и Q₂. Момент в силовом уравнении не участвует. Тогда силовое уравнение равновесия для нашей балки имеет вид:

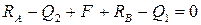
Подставим значения сил в уравнение:

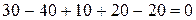
Уравнение тождественно выполняется, значит реакции найдены верно.

Таким образом, реактивные силы нашей балки направлены вверх и равны, соответственно:

, .

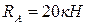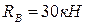Задача решена