Динамика вращательного движения твердого тела относительно неподвижной оси

Основные формулы

Момент силы 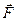относительно неподвижной точки О определяется векторным произведением радиус-вектора, проведенного из точки О в точку приложения силы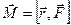

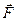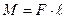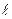Момент силы , действующей на тело, относительно оси вращения , где - плечо силы (кратчайшее расстояние от оси вращения до линии действия силы)

Основное уравнение динамики вращательного движения тела, вращающегося относительно неподвижной оси 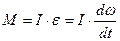, где -момент сил, приложенных к телу, момент инерции которого равен 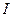, 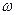- угловая скорость, 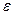- угловое ускорение, приобретаемое телом под действием вращающего момента.

ВОПРОСЫ И УПРАЖНЕНИЯ

1. Дайте определение и запишите формулу, определяющую момент силы относительно оси. Единицы измерения.

2. Сформулируйте закон сохранения импульса.

3. Запишите основное уравнение вращательного движения твердого тела относительно неподвижной оси.

ЗАДАЧИ

1. На барабан радиусом 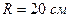, момент инерции которого 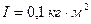, намотан шнур, к которому привязан груз массой 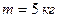. До начала вращения барабана высота груза над землей равна 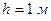. Найти ускорение грузов.

2. К ободу колеса 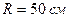и массой 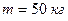приложена касательная сила в 10 Н. Найти: угловое ускорение колеса; через сколько времени после начала действия силы колесо будет иметь скорость, соответствующую ?

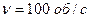3. Маховое колесо, имеющее момент инерции 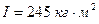, вращается, делая 20 об/с. После того, как на него перестал действовать вращающий момент сил, оно остановилось, сделав 1000 об. Найти: 1) момент сил трения; 2) время, прошедшее от момента прекращения действия вращающего момента, до полной остановки колеса.

4. Две гири массами 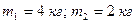соединены нитью и перекинуты через блок, момент инерции которого 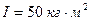и радиус 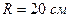. блок вращается с трением, момент сил трения равен 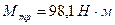. Найти разность сил натяжения нити по обе стороны блока и ускорение, с которым движутся грузы, если блок движется с постоянным угловым ускорением .

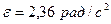5. Шар радиусом 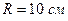и массой 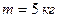вращается вокруг оси симметрии согласно уравнению 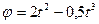. Определить момент сил для момента времени .

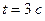6. Тонкий однородный стержень длиной 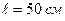и массой 400 г вращается с угловым ускорением 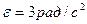около оси, проходящей перпендикулярно стержню через его середину. Определить вращающий момент.

7. Однородный диск радиуса R раскрутили до угловой скорости 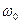и осторожно положили на шероховатую поверхность с коэффициентом трения 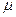. Сколько времени диск будет вращаться до остановки? Давление диска на поверхность считать равномерным.

8. С наклонной плоскости, составляющей с горизонтом угол 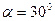, скатывается обруч. Длина наклонной плоскости 4 м. Найти скорость обруча в конце наклонной плоскости.

9. В условиях задачи 8 скатывается шар. Определить время скатывания с наклонной плоскости.

10. В условиях задачи 8 скатывается диск. Найти ускорение центра масс диска.

11. К точке, радиус-вектор которой относительно начала координат О равен 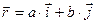, приложена сила 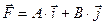, где 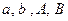- константы. Найти момент силы относительно точки О.

12. Тонкий однородный стержень массы 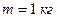и длины 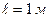падает без начальной скорости из вертикального положения в горизонтальное. Найти момент импульса стержня, когда он составляет с вертикалью угол .

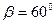13. 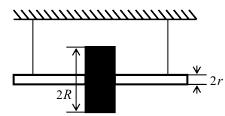Схема демонстрационного прибора (маятник Максвелла) изображена на рисунке. На валик радиусом 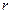наглухо насажен сплошной диск радиуса 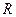и массой . Валик и диск сделаны из одного материала, причем выступающие из диска части оси имеют массу 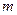. К валику прикреплены нити одинаковой длины, при помощи которых диск подвешивается к штативу. На валик симметрично наматываются нити в один ряд, благодаря чему диск поднимается, а затем свободно опускается. Найти ускорение, с которым опускается диск.

14. В схеме, изображенной на рисунке, считать блок массой сплошным цилиндром, тела массой 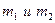- материальные точки. Нити невесомы и нерастяжимы. Трением пренебречь. Найти силы натяжения нитей в процессе движения.

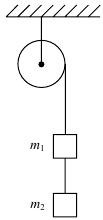
15. 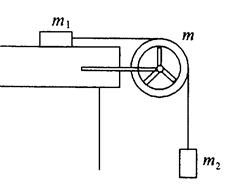Маховик, выполненный в виде диска радиусом 0,4 м и имеющий массу 100 кг, был раскручен до скорости вращения 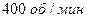и предоставлен самому себе. Под действием трения вала маховик остановился через 1 мин 20 с. Определить момент сил трения о подшипники.

16. Однородный шар массой М и радиусом R скатывается ( без проскальзывания) с наклонной плоскости. Чему будет равна скорость шара у основания наклонной плоскости? Высота наклонной плоскости H, угол с горизонтом .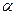

17. Тело массой 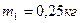, соединенное невесомой нитью посредством блока (в виде полого тонкостенного цилиндра) с телом массой 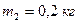, скользит по поверхности горизонтального стола. Масса блока 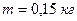. Коэффициент трения тела о поверхность равен 0,2. Пренебрегая трением в подшипниках, определите ускорение грузов.

18. 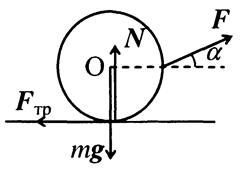Однородный шар радиусом 20 см скатывается без скольжения с вершины сферы радиусом 50 см. Определите угловую скорость шара после отрыва от поверхности сферы.

19. Однородный шар массой 4 кг движется поступательно по поверхности стола под действием постоянной силы, как показано на рисунке, где угол 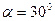. Коэффициент трения между шаром и столом равен 0,3. Найти величину силы и ускорение шара.

20. Однородный цилиндр радиуса 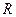раскрутили вокруг его оси до угловой скорости 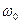и поместили затем в угол. Коэффициент трения между стенками угла и цилиндром равен 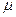. Найти: 1) сколько времени будет вращаться цилиндр; 2) сколько оборотов сделает цилиндр до остановки.

Семинар 10