Аксіоми та закони булевої алгебри
Булева алгебра базується на деяких аксіомах, із яких виводяться основні закони для перетворення виразів, що містять булеві змінні. Обґрунтування цих аксіом підтверджується таблицями істинності для розглядуваних операцій. Кожна аксіома подана у двох формах: кон’юнктивній і диз’юнктивній, що випливає із принципу двоїстості логічних операцій, згідно якого операції кон’юнкції і диз’юнкції допускають взаємну заміну, якщо одночасно поміняти логічну 1 на 0, а 0 на 1; знак Ú на Ù, а знак Ù на Ú.
Аксіоми кон’юнкції, диз’юнкції і заперечення:
1. 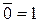 ; 1. 0 Ù 0 = 0; 1. 0 Ú 0 = 0;
; 1. 0 Ù 0 = 0; 1. 0 Ú 0 = 0;
2. 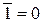 . 2. 0 Ù 1 = 0; 2. 0 Ú 1 = 1;
. 2. 0 Ù 1 = 0; 2. 0 Ú 1 = 1;
3. 1 Ù 0 = 0; 3. 1 Ú 0 = 1;
4. 1 Ù 1 = 1; 4. 1 Ú 1 = 1;
Закони булевої алгебри випливають із аксіом і також мають дві форми вираження: для кон’юнкції і для диз’юнкції.
Комутативні закони
а) 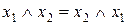 ; б)
; б) 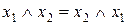 .
.
Сполучні закони
а) 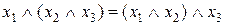 ; б)
; б) 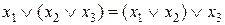 .
.
Розподільні закони
а) 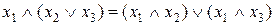 ; б)
; б) 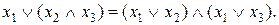
Закони поглинання
а) 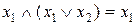 ; б)
; б) 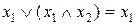 .
.
Закони склеювання
а) 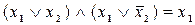 ; б)
; б) 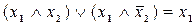 .
.
Закон подвійного заперечення
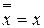 .
.
Закони де Моргана
а) 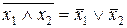 ; б)
; б) 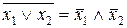
або після інвертування лівих і правих частин:
в) 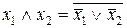 ; г)
; г) 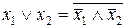 .
.
Зауважимо, що закони де Моргана є дійсними для будь-якої кількості змінних:
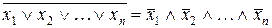 ;
; 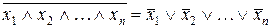 .
.
Закони ідемпотентності
а) 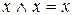 ; б)
; б) 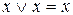 .
.
Закони універсальної множини
а) 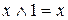 ; б)
; б) 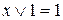 .
.
Закони нульової множини
а) 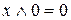 ; б)
; б) 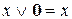 .
.
Закони доповнення
а) 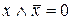 ; б)
; б) 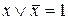 .
.
Правильність наведених законів легко доводиться за допомогою викладених вище аксіом або шляхом побудови таблиці істинності.
Доведемо, наприклад, справедливість розподільного закону (випадок б): 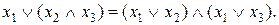
Спочатку виконаємо доведення скориставшись аксіомами:
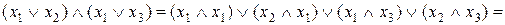
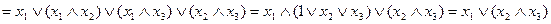 .
.
Доведемо шляхом побудови таблиці істинності. Для цього побудуємо таблиці істинності для виразів, які знаходяться в лівій і правій частинах рівності. Результати обчислень наведено в табл. 9.
Таблиця 9
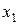 | 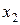 | 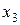 | 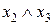 | 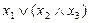 | 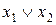 | 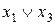 | 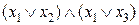 |
Співпадання значень у виділених стовпцях табл. 9 доводить справедливість рівності.
Аналогічно можна довести інші закони.
Із комутативного і асоціативного законів для диз’юнкції (кон’юнкції) випливає, що диз’юнкція (кон’юнкція) декількох змінних може виконуватись послідовно, причому порядок обчислення диз’юнкції не впливає на результат. Це дає можливість сформулювати такі правила:
1. Якщо в логічному добутку (кон’юнкції), що містить не менше двох співмножників, один із співмножників дорівнює нулю, то логічний добуток дорівнює нулю.
2. Якщо в логічному добутку, що містить не менше двох співмножників, є співмножник, який дорівнює одиниці, то цей співмножник можна вилучити.
3. Якщо в логічній сумі (диз’юнкції), що містить не менше двох доданків, є доданок, який дорівнює нулю, то цей доданок можна вилучити.
4. Якщо в логічній сумі, один із доданків дорівнює одиниці, то ця сума дорівнює одиниці.
Приклад 2. а) Довести, що 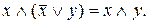 Маємо
Маємо
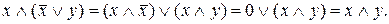
б). Довести, що 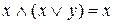 . Маємо
. Маємо
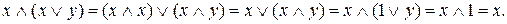
в) Довести, що 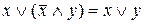 . Маємо
. Маємо
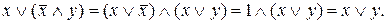
г) Довести, що 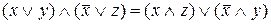 . Маємо
. Маємо
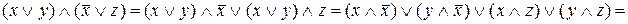
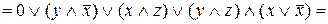
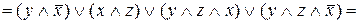
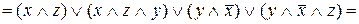
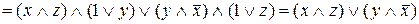 .
.
Двоїстість
Означення 1. Логічна функція 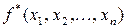 називається двоїстою до функції
називається двоїстою до функції 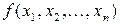 , якщо
, якщо 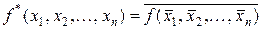 .
.
Означення 2. Функція, двоїста сама до себе, тобто 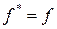 , називається самодвоїстою.
, називається самодвоїстою.
Правило побудови двоїстої функції. Для запису функції 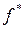 , двоїстої до функції
, двоїстої до функції 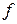 , треба у функції
, треба у функції 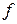 всюди 0 замінити на 1, 1 – на 0, знак Ù – на Ú, а знак Ú – на Ù. Наведене правило побудови двоїстих функцій називається принципом двоїстості.
всюди 0 замінити на 1, 1 – на 0, знак Ù – на Ú, а знак Ú – на Ù. Наведене правило побудови двоїстих функцій називається принципом двоїстості.
Приклад 3. Нехай, задано логічну функцію 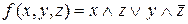 . Побудувати функцію двоїсту до заданої.
. Побудувати функцію двоїсту до заданої.
Розв’язання. а) Виходячи з означення двоїстості та застосувавши правило де Моргана два рази, одержимо
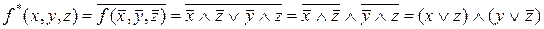 .
.
б) Скориставшись правилом побудови двоїстих функцій (принципом двоїстості) зразу одержимо, що 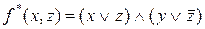 .
.
Легко переконатись, що таблиця істинності двоїстої функції 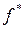 одержується з таблиці істинності для функції
одержується з таблиці істинності для функції 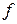 шляхом інвертування (заміною значень 0 на 1 та 1 на 0) значень функції й записом стовпчика інвертованих значень функції у зворотному порядку (див. два останні стовпці табл. 10)
шляхом інвертування (заміною значень 0 на 1 та 1 на 0) значень функції й записом стовпчика інвертованих значень функції у зворотному порядку (див. два останні стовпці табл. 10)
Таблиця 10
| x | y | z | 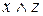 | 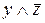 | 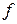 | 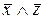 | 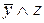 | 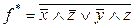 | 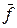 | 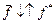 | ||
На підставі законів де Моргана можна вивести таке твердження: якщо функція 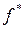 двоїста до функції
двоїста до функції 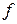 , то справедлива тотожність
, то справедлива тотожність
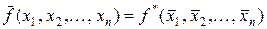 .
.
Таким чином, заперечення функції можна знайти або за допомогою закону де Моргана, або заміною в функції двоїстої до заданої значення всіх змінних на протилежні – 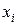 на
на 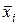 і
і 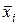 на
на 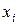 , де
, де 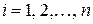 .
.
Логічна функція є самодвоїстою (непарною), якщо на кожній парі протилежних наборів вона приймає протилежні значення, тобто
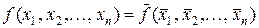 або
або 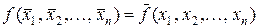 .
.
Для двох змінних такими функціями є: 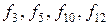 .
.
Приклад 4.Користуючись таблицею істинності вияснити чи є функція 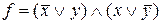 самодвоїстою.
самодвоїстою.
Розв’язання. Для побудови двоїстої функції скористаємось правилом побудови двоїстих функцій. Аналізуючи таблицю істинності (табл.11) легко переконатись, що побудована функція не є самодвоїстою, тобто: 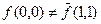 ,
, 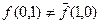 і
і 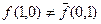 .
.
Таблиця 11
