Метод Эйлера модифицированный.

Для уменьшения погрешности вычислений часто используется модифицированный метод Эйлера. Этот метод имеет так же следующие названия: метод Эйлера-Коши или метод Рунге-Кутта второго порядка точности.

Пусть дано дифференциальное уравнение первого порядка

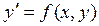
с начальным условием:

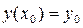
Выберем шаг h и введём обозначения:

x_i = x₀ + ih и y_i = y(x_i), где i = 0, 1, 2, ...,

x_i - узлы сетки,

y_i - значение интегральной функции в узлах.

При использовании модифицированного метода Эйлера шаг h делится на два отрезка.

Иллюстрации к решению приведены на рисунке 4.

Рисунок 4. Метод Эйлера модифицированный.

Проведем решение в несколько этапов:

1. Обозначим точки: А(х_i, y_i,), C(x_i + h/2, y_i + h/2 ∙ f(x_i, y_i)) и B(x_i+1, y_i+1);

2. Через точку А проведем прямую под углом α, где tg α = f(x_i, y_i);

3. На этой прямой найдем точку С(х_i + h/2, y_i + h/2 ∙ f(x_i, y_i));

4. Через точку С проведем прямую под углом α1, где tg α1 = f(x_i + h/2,y_i + h/2 ∙ f(x_i, y_i));

5. Через точку А проведем прямую, параллельную последней прямой;

6. Найдем точку B(x_i+1, y_i+1). Будем считать B(x_i+1, y_i+1) решением дифференциального уравнения при х = x_i+1;

7. После проведения вычислений, аналогичных вычислениям, описанным в методе Эйлера, получим формулу для определения значения у_i+1:

y_i+1 = y_i + h ∙ f(x_i + h/2, y_i + h/2 ∙ f(x_i, y_i)).

Модифицированный метод Эйлера дает меньшую погрешность. На рисунке 4 это хорошо видно. Так величина εl характеризует погрешность метода Эйлера, а ε - погрешность метода Эйлера модифицированного.

Блок-схема процедуры решения дифференциального уравнения методом Эйлера модифицированным приведена на рисунке 5.

EilerM(X0, Xk, Y0, N, Y)

F(x, у) - заданная функция - должна

быть описана отдельно.

h = (Xk – X0)/N

Входные параметры:
Х0, XК - начальное и конечное

i = 0, …, N-1

значения независимой

переменной;

x = X0 + i ∙ h

Y0 – значение y₀ из начального условия

y(x₀)=y₀;

Yi+1 = Yi + h ∙ F(x + h/2, Yi + h/2 ∙ F(xi, yi))

N - количество отрезков разбиения;

Выходные параметры:

Y - массив значений искомого решения

End

в узлах сетки.

Рисунок 5. Блок-схема процедуры решения дифференциального уравнения методом Эйлера модифицированным.

Решение поставленной задачи методами Эйлера и Эйлера модифицированного.

Метод Эйлера.

1. Строим оси координат;

2. Отмечаем A(0; -1.8) – первую точку интегральной кривой;

3. Ищем угол наклона касательной к графику в точке A:

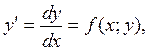
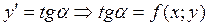
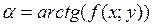
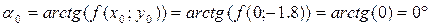
4. Строим касательную l₀ в точке А под углом α₀;

5. Находим х₁ по формуле: x_i = х₀ + ih, где h – шаг интегрирования

x₁ = 0 + 1 · 0,2 = 1,2;

6. Проводим прямую x = x₁ = 1,2 до пересечения с прямой l₀, отмечаем точку B(x₁; y₁);

7. Ищем y точки B:

Из прямоугольного треугольника ABC ,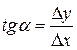

Δy = y₁ – y₀,

Δx = x₁ – x₀ = h,

f(x₀; y₀) = (y₁ – y₀)/h =>

y₁ = y₀ + h · (f(x₀; y₀)) = -1.8 + 0,2 · f(0;-1.8) = -1.8 + 0,2 · 0 = -1.8

Следовательно, точка B имеет координаты (1.2; -1.8).