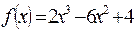Применение производной к построению графиков функций.

Алгоритм решения задачи на построение графика функции.

1. Найти область определения функции.

2. Найти производную функции.

3.Найти стационарные точки.

4. Определить знак производной на полученных интервалах.

5. Определить промежутки монотонности.

6. определить точки экстремумов и найти значение функции в этих точках.

7.Составить таблицу.

8. Найти дополнительные точки.

9. Построить график функции.

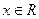
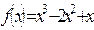Например.Исследовать функцию с помощью производной и построить её график.

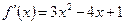1. ООФ:

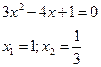
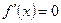2.

3.

9. .___+____.___-____.___+_______

1/3 1

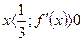9. , то функция возрастает;

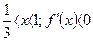, то функция убывает;

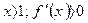, то функция возрастает;

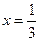6. – точка максимума, т.к. производная сменила знак с + на - ;

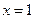- точка минимума, т.к. производная сменила знак с - на +.

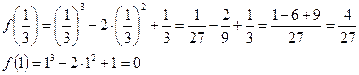
7.

х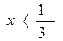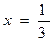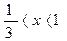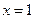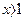
	+		-		+

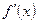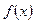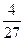8. Дополнительные точки:

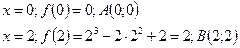9. Построение графика.

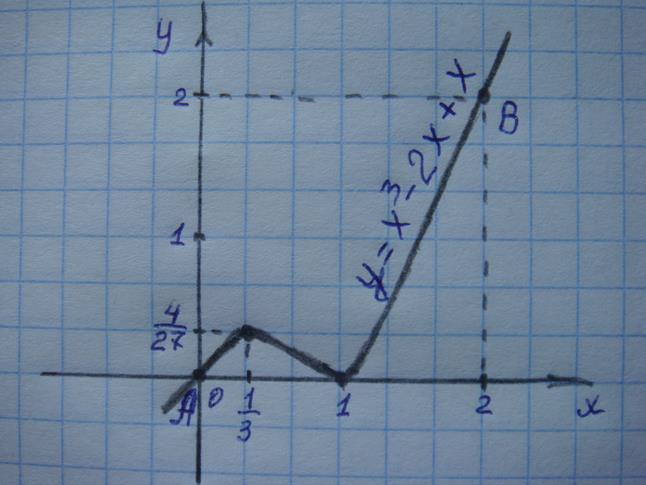
2.3. Варианты контрольных работ.

Контрольная работа № 1 по теме «Производная» В-1

1. Найти значение производной в точке х_0:

а) f(x) = 4x² +6x+3, x₀ = 1;

б) ;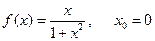

в) f(x) = (3x²+1) (3x²-1), х₀ =1;

г) f(x)=2x·cosx,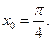

2. Найдите производную функции:

а) f(x)= 5^3x-4;

б) f(x) = sin (4x-7);

в) f(x) = ;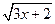

г) f(x) = ln (x³+5x).

3. Найти угловой коэффициент касательной к графику функции f(x) = 4 - x² в точке х₀ = -3.

4. Найти угол наклона касательной к графику функции 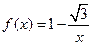в точке с абсциссой х₀= -1.

5. Напишите уравнение касательной к графику функции

f(x) = x² - 2x в точке с абсциссой х₀=-2.

6. Уравнение движения тела имеет вид s(t) = 2,5t² + 1,5t. Найдите скорость тела через 4 с после начала движения.

7.Исследовать функцию с помощью производной и построить график:

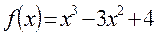
Контрольная работа № 1по теме «Производная» В-2

1. Найти значение производной в точке х_0:

а) f(x) = 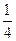х⁴ -3x²+5, x₀ = -3;

б) ;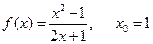

в) f(x) = (2x²+1) (4+х³), х₀ = 1;

г) f(x)=2x·sinx-1,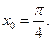

2. Найдите производную функции:

а) f(x)= 4^2x-1;

б) f(x) = сos(4x+5);

в) f(x) = ;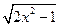

г) f(x) = 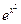+2x.

3. Найти угловой коэффициент касательной к графику функции f(x) = - 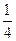x⁴ + x³ в точке х₀ = - 1.

4. В какой точке касательная к графику функции

f(x) =3x² -12х +11 параллельна оси абсцисс?

5. Напишите уравнение касательной к графику функции

f(x) = x³ - 3x² + 2х - 1 в точке с абсциссой х₀= 2.

6. Точка движется по прямолинейному закону x(t) = 2,5t² -10t + 11. В какой момент времени скорость тела будет равна 20? (координата измеряется в метрах, время – в секундах).

7. Исследовать функцию с помощью производной и построить график:

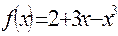
Контрольная работа №1 по теме «Производная» В-3

1. Найти значение производной в точке х₀

а) f(x) = 7x² -56x+8, x₀ = 4;

б) ;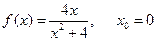

в) f(x) = (x²+1) (x³-2), х₀ = 1;

г) f(x)=3x·sinx,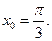

2. Найдите производную функции:

а) f(x)= 2^5x+3;

б) f(x) = сos(0,5x+3);

в) f(x) = ;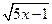

г) f(x) = 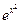+5x.

3. Найти угловой коэффициент касательной к графику функции f(x) = 2x² + x в точке х₀ = -2.

4. В какой точке касательная к графику функции f(x) =x²+4х - 12 параллельна оси абсцисс?

5. Напишите уравнение касательной к графику функции

f(x) = -x² -3x + 2 в точке с абсциссой х₀= -1.

6. Точка движется по прямолинейному закону x(t) = 3t² + t + 4. В какой момент времени скорость тела будет равна 7? (координата измеряется в метрах, время – в секундах)

7. Исследовать функцию с помощью производной и построить график:

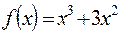
Контрольная работа № 1 по теме «Производная» В-4

1. Найти значение производной в точке х₀

а) f(x) = x⁵ -4x+8, x₀ = 2;

б) ;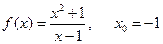

в) f(x) = (x³+7) (3x²-1), х₀ = –1;

г) f(x)=5x·cosx+2,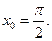

2. Найдите производную функции:

а) f(x)= 3^4x-1;

б) f(x) = 2sin (2,5x-2);

в) f(x) = ;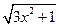

г) f(x) = ln (2x³+x).

3. Найти угловой коэффициент касательной к графику функции f(x) = 0,5x² + 1 в точке х₀ = 3.

4. Найти угол наклона касательной к графику функции 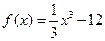в точке с абсциссой х₀ = 1.

5. Напишите уравнение касательной к графику функции

f(x) = x²+2x+1 в точке с

абсциссой х₀ = - 2.

6. Точка движется по прямолинейному закону x(t) = 4t + t² - 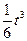. Найдите ее скорость в момент времени t=2 (координата измеряется в метрах, время – в секундах.)

7. Исследовать функцию с помощью производной и построить график:

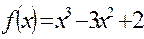
Контрольная работа № 1 по теме «Производная» В-5

1. Найти значение производной в точке х₀

а) f(x) = 3x⁵ -12x²+6х+2, x₀ = 1;

б) ;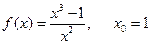

в) f(x) = (2x+1) (x-5), х₀ = 2;

г) f(x)=2x·cos3x,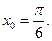

2. Найдите производную функции:

а) f(x)= 2^3x-4;

б) f(x) = sin (3x² - 2);

в) f(x) = ;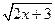

г) f(x) = ln (x²+5x).

3. Найти угловой коэффициент касательной к графику функции f(x) = 3х²+40х -10 в точке х₀ = -1.

4. Найти угол наклона касательной к графику функции

f(x) = 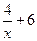в точке с абсциссой х₀ = - 1.

5. Напишите уравнение касательной к графику функции

f(x) = x²-2x +3в точке с абсциссой х₀= - 2.

6. Точка движется по прямолинейному закону x(t) = 3t³+2t+1. Найдите ее скорость в момент времени t = 2 (координата измеряется в метрах, время – в секундах.)

7. Исследовать функцию с помощью производной и построить график:

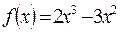
Контрольная работа № 1 по теме «Производная» В-6

1. Найти значение производной в точке х₀

а) f(x) = 5x³ -6x⁴+3х²+1, x₀ = 1;

б) ;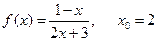

в) f(x) = (x²+1) (x³-2), х₀ = 1;

г) f(x)=2x·sin5x,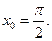

2. Найдите производную функции:

а) f(x)= 2^3x+5_,

б) f(x) = сos(3x-1);

в) f(x) = ;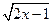

г) f(x) = 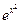-2x.

3. Найти угол наклона касательной к графику функции

f(x) = 3x³ -35x+8 в точке х₀ = 2.

4. В какой точке касательная к графику функции f(x) =x³ -3х+1 параллельна оси абсцисс?

5. Напишите уравнение касательной к графику функции

f(x) = x²+3x-2 в точке с абсциссой х₀ = -1.

6. Точка движется по прямолинейному закону x(t) = 3t² -2t+4. В какой момент времени скорость тела будет равна 4? (координата измеряется в метрах, время – в секундах)

7. Исследовать функцию с помощью производной и построить график:

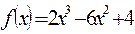
Контрольная работа №3 по теме «Производная» В-7

1. Найти значение производной в точке х₀

а) f(x) = 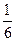x⁶ -3x²+2, x₀ = 2;

б) ;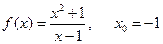

в) f(x) = (x³-4) (3x²+1), х₀ = 2;

г) f(x)=5x·cosx+2,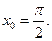

2. Найдите производную функции:

а) f(x)= 3^{4x + 2};

б) f(x) = 2sin (5х+2);

в) f(x) = ;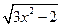

г) f(x) = ln (3x²- x).

3. Найти угловой коэффициент касательной к графику функции f(x) = 0,5x² -1 в точке х₀ = - 3.

4. Найти угол наклона касательной к графику функции 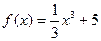в точке с абсциссой х₀ = -1.

5. Напишите уравнение касательной к графику функции

f(x) = x²+2x+1 в точке с абсциссой х₀ = - 2.

6. Точка движется по прямолинейному закону x(t) = 4t - t²+ 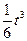. Найдите ее скорость в момент времени t = 2 (координата измеряется в метрах, время – в секундах.)

7. Исследовать функцию с помощью производной и построить график:

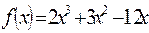
Контрольная работа № 1 по теме «Производная» В-8

1. Найти значение производной в точке х₀

а) f(x) = 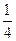х⁴ -2x³+5х-1, x₀ = 2;

б) ;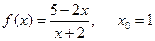

в) f(x) = (2x²+1) (1+х³), х₀ = 2;

г) f(x)=2x·sinx-1,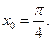

2. Найдите производную функции:

а) f(x)= 5^{2x +3}_,

б) f(x) = сos(5x²+1);

в) f(x) = ;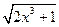

г) f(x) = 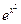+5x.

3. Найти угловой коэффициент касательной к графику функции f(x) = 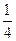x⁴ -x² в точке х₀ = 1.

4. Найти угол наклона касательной к графику функции

f(x) = 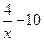в точке с абсциссой х₀ = 2.

5. Напишите уравнение касательной к графику функции

f(x) = x³-3x²+2х в точке с абсциссой х₀ = 2.

6. Точка движется по прямолинейному закону x(t) = 2,5t² - 10t +6. Найти скорость тела в момент времени t = 4 (координата измеряется в метрах, время – в секундах).

7. Исследовать функцию с помощью производной и построить график:

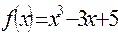
Контрольная работа № 1 по теме «Производная» В-9

1.Найти значение производной в точке х₀

а) f(x) = 6x³ +8x+9, x₀ = 7;

б) ;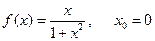

в) f(x) = (5x+1) (3x²-4), х₀ =0;

г) f(x)=6x·sinx,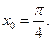

2.Найдите производную функции:

а) f(x)= 8^7x-8;

б) f(x) = cos (3x+1);

в) f(x) = 5 ;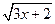

г) f(x) = ln (x²+4x).

3.Найти угловой коэффициент касательной к графику функции f(x) = 4x- x³ в точке х₀ = 0.

4.Найти угол наклона касательной к графику функции 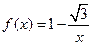в точке с абсциссой х₀= -1.

5.Напишите уравнение касательной к графику функции f(x) = 7x² - 4x в точке с абсциссой х₀=-3.

6.Уравнение движения тела имеет вид s(t) = 2t² + t. Найдите скорость тела через 4 с после начала движения.

7.Исследовать функцию с помощью производной и построить график:

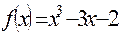
Контрольная работа № 1 по теме «Производная» В-10

1.Найти значение производной в точке х₀

а) f(x) = 2х³+4x²-6, x₀ = -4;

б) ;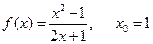

в) f(x) = (x²+3) (2+х⁴), х₀ = -1;

г) f(x)=3x·cosx-2,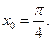

2.Найдите производную функции:

а) f(x)= 6^3x+1;

б) f(x) = sin(2x-3);

в) f(x) = ;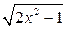

г) f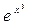(x) = -4x.

3.Найти угловой коэффициент касательной к графику функции f(x) = -4x⁴ + 2x² в точке х₀ = - 2.

4.В какой точке касательная к графику функцииf(x) =3x² -12х +11 параллельна оси абсцисс?

5.Напишите уравнение касательной к графику функции

f(x) = 2x³ +5x² – 3x - 13 в точке с абсциссой х₀= 3.

6.Точка движется по прямолинейному закону x(t) = 2,5t² -10t + 11. В какой момент времени скорость тела будет равна 20? (координата измеряется в метрах, время – в секундах).

7. Исследовать функцию с помощью производной и построить график: