Вероятность появления хотя бы одного события

При решении задач иногда требуется найти вероятность того, что произойдет хотя бы одно событие из нескольких. В этом случае метод решения зависит от того, какие эти события.

Если события независимые, то используется формула

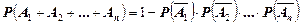(13)

Если события несовместимые, то применяется формула

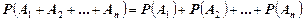(14)

Если два события совместимые, то используется формула

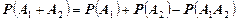. (15)

Пример 15. Прибор содержит два независимо работающих элемента. Вероятность отказа первого элемента равна 0,05, второго-0,08. Найти вероятность отказа прибора, если для этого достаточно, чтобы отказал хотя бы один элемент.

Решение. Обозначим события:

А – отказал хотя бы один элемент, то есть либо один, либо оба элемента,

А₁ – отказал первый элемент,

А₂ – отказал второй элемент.

События А₁ и А₂ независимы. В этом случае проще сначала найти вероятность противоположного события 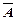, которое состоит в том, что ни одного из событий А₁, и А₂ не произошло: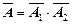

Тогда 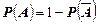или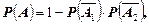

здесь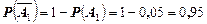

.

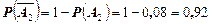Окончательно получим

.

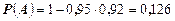Повторение независимых опытов. Формула Бернулли

Если производится n независимых опытов, причем в каждом событие А появляется с одной и той же вероятностью р, то вероятность того, что событие А появится ровно m раз в этих n опытах, находится по формуле Бернулли:

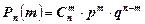, (16)

здесь , .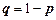

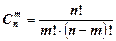Пример 16. Партия товара содержит 20 изделий первого сорта и 10 изделий второго сорта. Вынимают подряд 4 изделия, возвращая каждое назад. Найти вероятность того, что из 4-х вынутых изделий:

а) два окажутся первого сорта;

в) не менее двух окажутся первого сорта.

Решение. Обозначим события:

А – два из четырех вынутых изделий первого сорта,

В – не менее двух изделий из четырех вынутых первого сорта.

Так как взятое изделие каждый раз возвращается назад, то вероятность вынуть изделие первого сорта постоянна и равна

.

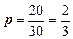Тогда вероятность противоположного события

.

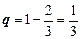Теперь по формуле Бернулли найдем

.

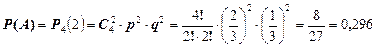Событие В означает, что из 4-х взятых изделий либо 2, либо 3, либо 4 изделия первого сорта. Тогда 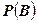найдем как сумму

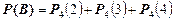
Здесь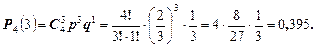

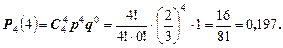
Окончательно получим .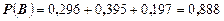

Локальная теорема Лапласа

В том случае, когда число повторений опытов слишком велико, применение формулы Бернулли неудобно. В этом случае для приближенного нахождения вероятности появления события А равно к раз в n опытах используется формула Лапласа

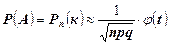, где (17)

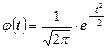при .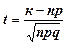

Здесь функция 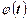находится по специальным таблицам при разных значениях 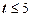. При 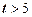функция 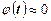. Следует иметь ввиду, что .

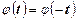Пример 17. Партия товара состоит из 200 изделий двух сортов. Вероятность вынуть изделие первого сорта равна 0,48. Найти вероятность того, что во всей партии товара окажется 95 изделий первого сорта (событие А).

Решение. Так как число 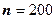велико и вероятность события постоянна 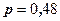, то используется формула Лапласа

.

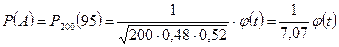Найдем значение параметра t: .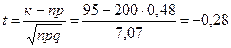

Теперь по таблице найдем : .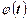

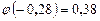Окончательно получим 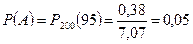.