Ііі. жаңа сабақты түсіндіру.
№3
 Берілгені: АВСД төртбұрыш, ВД – диогоналі
Берілгені: АВСД төртбұрыш, ВД – диогоналі
 ,
,  ,
, 
Табу керек: ВД
Шешуі:  ,
,
 екеуін қоссақ
екеуін қоссақ



V. Қорытынды.Оқушылардың өткен материалды еске түсіру нәтижелерін сұрақ-жауап арқылы анықтау.
1) Қандай фигура төртбұрыш деп аталады?
2) Төртбұрыштың қандай төбелері – көршілес, қандайлары қарама-қарсы төбелер деп аталады?
3) Төртбұрыштың диогоналі деген не?
4) Төртбұрыштың қандай қабырғалары көршілес, қандай қабырғалары қарама-қарсы қабырғалар деп аталады?
5) Төртбұрыш қалай белгіленеді?
VІ. Үйге тапсырма. §1. №3
VIІ. Бағалау. Оқушылардың білім-біліктілігін анықтап баға қою.
8- сынып.Геометрия.
Сабақ-. мерзімі-
Сабақтың тақырыбы:Есеп шығару.
Сабақтың мақсаты:
а)Білімділік: Төртбұрыштың түрлерімен, элементтерімен танысу.
ә) Дамытушылық: Төртбұрыштың элементерінің берілген қатынастары бойынша есептеуді үйрену.
б) Тәрбиелік:оқушылардың ой-өрісін кеңейту,төзімділікке тәрбиелеу.
Сабақтың әдісі:практикалық
Сабақтың типі:аралас
Сабақтың көрнекілігі:сызба,жазба материалдар
Сабақтың барысы: І.Ұйымдастыру кезеңі. Оқушылардың сабаққа қатысуын,дайындығын тексеру.Оқушылармен амандасу.
ІІ.Өткенді қайталау.
1.Қандай фигураны төртбұрыш деп атайды ?
2. Төртбұрыштың қандай элементтерін білесіңдер?
3. Төртбұрыш қандай түрге бөлінеді?
4. Дөңес төртбұрыш дегеніміз не ?
5. Дөңес емес төртбұрыш дегеніміз не ?
Үй тапсырмасын тексеру
№3. төртбұрыш диагоналі арқылы екі үшбұрышқа бөлінген. Егер үшбұрыштардың және төртбұрыштардың периметрлері сәйкесінше 30 м, 34 м және 36 м онда төртбұрыштың диагоналі неге тең ?
АВ + ВС + АС = 30
АD + DС + АС = 34
АВ + ВС + АD + DС = 36
АВ + ВС = 30 – АС ; AD + DС = 34 – АС
30 – АС + 34 – АС = 36
2АС = 64 – 36 ; 2АС = 28; АС = 14
ІІІ. Есеп шығару.
№5. Төртбұрыштың қабырғаларының қатынасы 4 : 5 : 8 : 2, ал оның периметрі 57 дм. Төртбұрыштың қабырғаларын табыңдар.(12 дм; 15 дм; 24 дм; 6 дм)
№8. Егер төртбұрыштың бұрыштарының қатынасы 1) 3 : 5 : 6 : 1;
2) 6 : 7 : 8 : 9 болса, оның бұрыштары қандай?
Жауабы: 1) 720; 1200; 1440; 240; 2) 720; 840; 960; 1080
№9. Төртбұрыштың екі бұрышының қатынасы 5 : 7 қатынасындай, үшінші бұрышы олардың айырымына тең, ал төртінші бұрыш үшінші бұрыштан
240-қа кіші. Төртбұрыштың бұрыштарын табыңдар
(5х + 7х + 2х + 2х – 240 = 3600; 16х = 3840; х = 240;
1200; 1680; 480; 240)
№10

Берілгені: MNKF төртбұрыш.

 ,
, 
Табу керек: 
Шешуі:


ІV. Сабақты қорытындылау.
V. Үйге: §1,№9,
VІ.Бағалау.Оқушыларды сұрақ-жауап алып бағалау
8-сынып.Геометрия.
Сабақ-5.мерзімі-
Сабақтың тақырыбы: Параллелограмм және оның қасиеттері
Сабақтың мақсаты:
а)Білімділік: Параллелограмм және оның элементтері туралы түсінік.
ә) Дамытушылық: Параллелограмм элементтерінің арасындағы қатынастарды көрсететін есептер шығару
б) Тәрбиелік: Оқушыларды жылдам ойлауға, жауапкершілікті сезінуге тәрбиелеу.
Сабақтың әдісі:түсіндірмелі – көрнекілік
Сабақтың типі:жаңа сабақ
Сабақтың көрнекілігі:сызба,жазба материалдар
Сабақтың барысы: І.Ұйымдастыру кезеңі. Оқушылардың сабаққа қатысуын,дайындығын тексеру.Оқушылармен амандасу.
ІІ.Өткенді қайталау.
1. Қандай фигура төртбұрыш деп аталады?
2.Төртбұрыштың қандай төбелері – көршілес, қандайлары қарама-қарсы төбелер деп аталады?
3.Төртбұрыштың диогоналі деген не?
4.Төртбұрыштың қандай қабырғалары көршілес, қандай қабырғалары қарама-қарсы қабырғалар деп аталады?
5.Төртбұрыш қалай белгіленеді?
Бүгінгі өтетін тақырыбымыз дөңес төртбұрыштың бір түрі параллелограмм.
Параллелограмм тақырыбын өтпес бұрын параллель түзулер, үшбұрыштар теңдігінің белгілері, перпендикуляр, периметр, диагональ деген ұғымдарды еске түсіріп өтейік.
ІІІ. Жаңа сабақ.
Анықтама. Қарама-қарсы қабырғалары қос-қостан параллель болатын төртбұрыш параллелограмм деп аталады. Параллелограмның бір төбесінен қарсы жатқан қабырғасына түсірілген перпендикуляр оның биіктігі деп аталады, ал биіктік түсірілген қабырға табаны деп аталады.
2-теорема(1-қасиет). Параллелограмның қарама-қарсы қабырғалары тең және қарама-қарсы бұрыштары да тең (тең үшбұрыштардың сәйкес бұрыштары тең болғандықтан)





(2-қасиет)Параллелограмның диагональдары қиылысу нүктесінде қақ бөлінеді. (Себебі ΔАВО = ΔСDО
 (АВ = DС,
(АВ = DС, 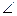 1=
1= 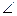 2,
2, 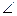 6 =
6 = 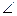 5), АО = ОС, ВО = ОD болады.
5), АО = ОС, ВО = ОD болады.
(3-қасиет) Параллелограмның бір қабырғасына іргелес бұрыштарының қосындысы 1800-қа тең.
IV. Жаңа сабақты бекітуге есептер шығару.
Ауызша №11, 12 есептер
№13. а || в түзулері берілген. Оларды сәйкесінше А, В, С және D нүктелерінде қиып өтетін c || d екі түзу жүргізіңдер. Нәтижесінде, АВСD төртбұрышын аламыз. Осы төртбұрыштың параллелограмм болатынын түсіндіріп беріңдер. Суретін салып көрсетіңдер.
№15. 1) Қабырғалары 6 см және 4 см; 2) 11,5 м және 7 м болатын параллелограмның периметрі қандай? (20 см; 37 м)
№16. Параллелограмның бір қабырғасы 12,4 дм. 1) Екінші қабырғасы одан 0,8 дм қысқа; 2) 1,6 дм ұзын ; 3) 4 есе кіші. Параллелограмның периметрі неге тең?(48 дм; 52,8 дм; 31 дм)
 (1)
(1)
Берілгені:  параллелограмм
параллелограмм

Табу керек: 
Шешуі: 

Жауабы: 48 дм
 №17. Параллелограмның периметрі 18,4 дм. Оның бір қабырғасы : 1) 3 дм; 2) 7 дм. Екінші қабырғасын табыңдар.(6,2 дм; 2,2 дм)
№17. Параллелограмның периметрі 18,4 дм. Оның бір қабырғасы : 1) 3 дм; 2) 7 дм. Екінші қабырғасын табыңдар.(6,2 дм; 2,2 дм)
(1)Берілгені:  параллелограмм
параллелограмм 

Табу керек: АД
Шешуі:

Жауабы: 6,2 дм
 №18. Параллелограмның периметрі 24 см. Оның бір қабырғасы екінші қабырғасынан : 1) 4 см ұзын; 2) 6 см қысқа; 3) 2 есе ұзын. Параллелограмның қабырғаларын табыңдар.(1) 4 см; 8 см; 2) 9 см; 3 см; 3) 4 см; 8 см)
№18. Параллелограмның периметрі 24 см. Оның бір қабырғасы екінші қабырғасынан : 1) 4 см ұзын; 2) 6 см қысқа; 3) 2 есе ұзын. Параллелограмның қабырғаларын табыңдар.(1) 4 см; 8 см; 2) 9 см; 3 см; 3) 4 см; 8 см)
(1)
Берілгені:  параллелограмм
параллелограмм


Табу керек: 
Шешуі: АВ=x деп белгілейік
АД=x+4


Жауабы: 4 см, 8 см
V. Сабақты қорытындылап, бағалау.
Қандай төртбұрыш параллелограмм деп аталады?
Параллелограмның қандай қасиеттерін білесіңдер?
VІ.Үйге тапсырма: §2 (белгілеріне дейін оқу), №16(2), №17(2), №18(2) .
8- сынып.Геометрия.
Сабақ-6. мерзімі-
Сабақтың тақырыбы:Есеп шығару.
Сабақтың мақсаты:
а)Білімділік: Параллелограмм анықтамасын, қасиеттерін есептер шығаруда қолдану
ә) Дамытушылық: Оқушылардың ой өрісін, есте сақтау, сызбамен жұмыс істеу қабілеттерін, дағдыларын дамыту.
б) Тәрбиелік: Оқушыларды ұқыптылыққа, шыдамдылыққа, нәтиже алуға баулу.
Сабақтың әдісі:практикалық
Сабақтың типі:аралас
Сабақтың көрнекілігі:сызба,жазба материалдар
Сабақтың барысы: І.Ұйымдастыру кезеңі. Оқушылардың сабаққа қатысуын,дайындығын тексеру.Оқушылармен амандасу.
ІІ.Өткенді қайталау.
1. Параллелограмм деген не?
2. Параллелограмм қасиеттері 3-теорема. Егер дөңес төртбұрыштың :
1) қарама-қарсы қабырғалары тең болса, онда ол параллелограмм болады (үшбұрыштар теңдігінің 3-белгісі бойынша);
2) қарама-қарсы бұрыштары тең болса, онда ол параллелограмм болады (төртбұрыштың ішкі бұрыштарының қосындысы 3600-қа тең болатынына);
3) диагональдары қиылысу нүктесінде тең екіге бөлінсе, онда ол параллелограмм болады (үшбұрыштар теңдігінің 1-белгісі бойынша);
4) бір қабырғасына іргелес бұрыштарының қосындысы 1800-қа тең болса, онда ол параллелограмм болады (түзулердің параллельдік белгісі бойынша).
4-теорема. Егер дөңес төртбұрыштың қарама-қарсы екі қабырғасы тең және параллель болса, онда ол параллелограмм болады.
Параллелограмм қарсы қабырғалары тең болатынын дәлелдеу
3. Параллелограмм диагональдары қиылысу нүктесінде қақ бөлінетінін дәлелдеу
4. Параллелограмның периметрінің формуласы
Үй тапсырмасын тексеру
№16. Параллелограмның бір қабырғасы 12,4 дм. 2) 1,6 дм ұзын . Параллелограмның периметрі неге тең?( 52,8 дм )
№17. Параллелограмның периметрі 18,4 дм. Оның бір қабырғасы : 2) 7 дм. Екінші қабырғасын табыңдар.(2,2 дм)
№18. Параллелограмның периметрі 24 см. Оның бір қабырғасы екінші қабырғасынан : 2) 6 см қысқа. Параллелограмның қабырғаларын табыңдар.
( 9 см; 3 см)
ІІІ. Есеп шығару.
№19 (1). Параллелограмның екі қабырғасының қосындысы 12 см, ал олардың қатынасы 1 : 2. Параллелограмның қабырғалары неге тең?
 Берілгені: ABCD параллелограмм
Берілгені: ABCD параллелограмм
AB+AD=12см
AB:AD=1:2
Т/к: AB, AD-?
Шешуі: AB=x, AD=2x
x+2x=12 x=4
AB=4см, AD=8 см
Жауабы: 4 см, 8 см
№21. (2) Параллелограмның бір бұрышы екінші бұрышынан : 2) 70 30 '-қа кіші. Параллелограмның бұрыштарын есептеңдер ( 93045'; 86015')
 Берілені: ABCD параллелограмм
Берілені: ABCD параллелограмм
<А < <В
<А= <B – 7030 '
Т/к: <A, <B, <C, <D - ?
Шешуі: <А + <В = 1800
<B − 7030 ' + <B =1800
2 <B = 187030 '
< B=93045'
<A = 93045' – 7030 ' = 86015'
Жауабы: <A = <C = 86015'
<B = <D = 93045'
№27. АВСD параллелограмында А бұрышының биссектрисасы ВС қабырғасын Е нүктесінде қиып өтеді. АВ = 12 дм және АD = 17 дм деп алып, ВЕ және ЕС кесінділерінің ұзындығын есептеңдер.
Параллелограмның бір қабырғасында жатқан нүктелер оның қарсы қабырғасынан бірдей қашықтықта жатады. Сондықтан ВЕ = 12 дм, ал
ЕС = 5 дм.
Қосымша есептер:
№1. Екі бұрышының қосындысы 1) 800, 2) 1600 болатын параллелограмның барлық бұрыштарын табыңдар.
№2. Екі бұрышының айырмасы 1) 700, 2) 1100 болатын параллелограмның барлық бұрыштарын табыңдар.
ІV.Қорытынды.Сабақты бекіту.
Қандай төртбұрыш параллелограмм деп аталады?
Параллелограмның қандай қасиеттерін білесіңдер?
Параллелограмның қасиеттері мен белгілерін тұжырымдаңдар.
V.Үйге тапсырма. §2, №19(2), 21 (1,3), №28
VІ.Бағалау. Оқушыларды сұрақ-жауап алып бағалау
3. Параллелограмның диагоналі оның екі қабырғасымен 250 және 350 болатын бұрыштар жасайды. Параллелограмның бұрыштарын табыңдар.
№4. ABCD параллелограмның периметрі 10 см-ге тең. ABD үшбұрышының периметрі 8 см-ге тең екені белгілі. BD диагоналінің ұзындығын табыңдар.
8-сынып.Геометрия.
Сабақ-7.мерзімі-
Сабақтың тақырыбы: Тіктөртбұрыш
Сабақтың мақсаты:
а)Білімділік: Тіктөртбұрыштың анықтамалары және қасиеттері туралы түсінік
ә) Дамытушылық: Тіктөртбұрыштың қасиеттерін қолдану арқылы есептер шығару
б) Тәрбиелік: Оқушыларды жылдам ойлауға, жауапкершілікті сезінуге тәрбиелеу.
Сабақтың әдісі:түсіндірмелі – көрнекілік
Сабақтың типі:жаңа сабақ
Сабақтың көрнекілігі:сызба,жазба материалдар
Сабақтың барысы: І.Ұйымдастыру кезеңі. Оқушылардың сабаққа қатысуын, дайындығын тексеру. Оқушылармен амандасу.
ІІ.Өткенді қайталау.
Бұрыш, тік бұрыш, төртбұрыш, параллелограмм, диагональ, периметр, перпендикуляр, тікбұрышты үшбұрыштар теңдігінің белгілерін еске түсіру.
Үй тапсырмасын тексеру
№19 (2) ауызша тексеру.
 Параллелограмның екі қабырғасының қосындысы 12 см, ал олардың қатынасы 3:2. Параллелограмның қабырғаларын тап. Берілгені: ABCD – параллелограмм AD:AB=3:2 AD+AB=12 см Т/к: AB, AD-?
Параллелограмның екі қабырғасының қосындысы 12 см, ал олардың қатынасы 3:2. Параллелограмның қабырғаларын тап. Берілгені: ABCD – параллелограмм AD:AB=3:2 AD+AB=12 см Т/к: AB, AD-?
Шешуі: AD=3x. AB=2x; 3x+2x=12; 5x=12; x=2,4
AB=2∙2.4=4.8 см, AD=3∙2.4=7.2 см; Жауабы: 4,8см, 7,2 см
 №21 (1;3) Параллелограмның бір бұрышы екінші бұрышынан 1) 150-қа, 3)2 есе үлкен. Параллелограмның бұрыштарын табыңдар.
№21 (1;3) Параллелограмның бір бұрышы екінші бұрышынан 1) 150-қа, 3)2 есе үлкен. Параллелограмның бұрыштарын табыңдар.
Берілгені: ABCD – параллелограмм
<B = <A+150
Т/к: <A, <B, <C,<D-?
Шешуі: <A = <C = x
<B = <D = x+150
Параллелограмның қасиеті бойынша
<A + <B =1800; x+x++150 =1800; 2x = 1650 ; x = 82030'
<A = <C = 82030' , <B = <D = 82030' + 150 = 97030'
Жауабы: <A = <C = 82030'; <B = <D = 97030'
2) <B = 2<A ; <A = x; <B = 2x; <A+<B = 1800
x + 2x = 1800; 3x = 1800; x=600 ; <A = 600, <B =1200
№26. Параллелограмның бір бұрышының биссектрисасы қабырғаны 12 см және 7 см кесінділерге бөледі. Параллелелограмның периметрін табыңдар.  Берілгені: ABCD – параллелограмм АК-биссектриса
Берілгені: ABCD – параллелограмм АК-биссектриса
1 жағдай: BK=12см, KC=7 см
2 жағдай: BK=7 см, KC=12см
Т/к: PABCD-?
Шешуі: PABCD=2 (AB+BC)
BC=BK+KC=19см
ΔABK-тең бүйірлі болғандықтан BK=AB=12см
P=2 (19+12)=2∙31=62 см
2 жағдай: BK=7см, KC=12см
AB=BK=7
PABCD=2 (7+19)=2∙26= 52
Жауабы: 62 см немесе 52 см
ІІІ. Жаңа сабақты түсіндіру.
Анықтама:Барлық бұрыштары тік болатын параллелограмды тіктөртбұрыш деп атайды.
Анықтамадан тіктөртбұрыш параллелограмның дербес жағдайы екені белгілі, олай болса параллелограмның барлық қасиеттері тіктөртбұрыштың қасиеттері болады. Онда «параллелограмм» сөзінің орнына «тіктөртбұрыш» деп қойып қасиеттерін айтып шығыңдар. (Оқушылардан сұралады)
1-қасиет: Тіктөртбұрыштың қарама-қарсы қабырғалары тең
2-қасиет: Диагональдары оны тең екі үшбұрышқа бөледі
3-қасиет: Диагональдары қиылысу нүктесінде тең екіге бөлінеді.
4-қасиет: Бір бұрышының биссектрисасы тең бүйір үшбұрыш түзеді.
Осы қасиеттерден басқа тіктөртбұрышқа тән қасиеттер:
«Тіктөртбұрыштың диагональдары тең болады.»


 В С Берілген:
В С Берілген:
АВСD- тіктөртбұрыш
Д/К: АС = ВD
Дәлелдеу: ΔВАD мен ΔСDА
қарастырамыз.
А Д
Бұл тік бұрышты үшбұрыштарды <А = <D = 900
АВ = DС. АD-ортақ. Екі катеті бойынша ΔВАD мен ΔСDА. Онда оның қалған элементтері де тең, гипотенузалары ВD = АС: бізге дәлелдеу керегі де осы еді.
Тік төртбұрыштың белгілері:
1 белгісі: Егер параллелограмның диагональдары тең болса, онда ол тіктөртбұрыш болады.
 Берілгені: АВСD параллелограмм
Берілгені: АВСD параллелограмм
АС = ВD
Дәлелдеу керек: 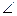 А=
А= 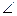 В=
В= 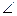 С=
С= 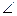
 =900
=900
Дәлеледеу: АС=  - шарт бойынша, параллелограмм қасиеттері бойынша
- шарт бойынша, параллелограмм қасиеттері бойынша
АО = ОС, ВО =  , АО = ОС = ВО. ΔВОС, ΔАОВ- теңбүйірлі үшбұрыштар, бұдан <2=<4. <1=<3. Ал ΔАВС- ның ішкі бұрыштарының қосындысы
, АО = ОС = ВО. ΔВОС, ΔАОВ- теңбүйірлі үшбұрыштар, бұдан <2=<4. <1=<3. Ал ΔАВС- ның ішкі бұрыштарының қосындысы
<3+<1+<2+<4=1800
2 (<1+<2)=1800
<1+<2=900 <АВС=900
Онда 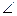 А=
А= 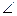 В=
В= 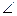 С=
С= 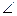
 =900 теорема дәлелденді.
=900 теорема дәлелденді.
2 белгісі: Егер параллелограмның бір бұрышы тік болса, онда ол тіктөртбұрыш болады.
3 белгісі: Егер төртбұрыштың үш бұрышы тік болса, онда ол тік төртбұрыш болады.
Тіктөртбұрыштың төбелері арқылы өтетін шеңбер болады. Оның центрі диагоналдардың қиылысу нүктесі болады.
|


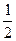 АС=
АС=