ОБЫКНОВЕННЫЕ Дифференциальные уравнения

Пример 19.1. Предельные затраты однопродуктовой фирмы заданы соотношением .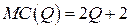

Найти функцию полных затрат 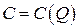, если фиксированные издержки 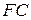фирмы составляют 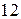ден. ед.

Решение. Напомним, что предельные издержки равны 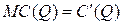. Это значит, что полные издержки можно найти путем интегрирования функции предельных издержек: .

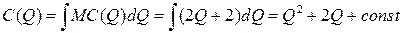Условие 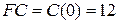позволяет определить значение 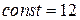. Таким образом, получаем функцию полных издержек .

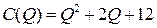Ответ: .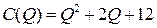

Пример 19.2. Предельный доход однопродуктовой фирмы от реализации производимой продукции задан соотношением .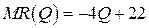

Найти функцию дохода .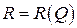

Решение. Напомним, что предельный доход равен 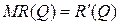. Это значит, что функцию дохода можно найти путем интегрирования функции предельного дохода: .

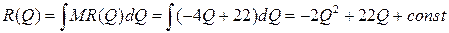Условие 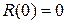(если фирма ничего не продает, то ее доход равен нулю) позволяет определить значение 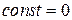. Таким образом, получаем функцию дохода формы .

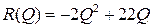Ответ: .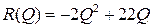

Задача 19.

Предельные затраты однопродуктовой фирмы заданы соотношением 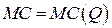. Найти функцию полных затрат 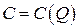, если известны фиксированные издержки 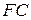фирмы.

19.1. ;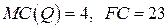

19.2. ;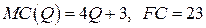

19.3. ;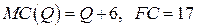

19.4. ;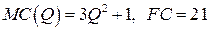

19.5. .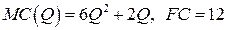

Предельный доход однопродуктовой фирмы от реализации производимой продукции задан соотношением 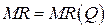. Найти функцию дохода .

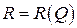19.6. ;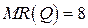

19.7. ;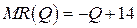

19.8. ;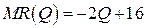

19.9. ;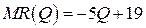

19.10. .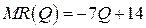

Пример 20. Динамика процентной ставки 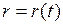определяется уравнением 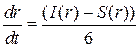,где функцияинвестиций 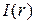задана в виде 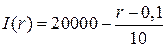, а функция сбережений .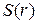

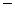
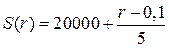Вывести уравнение динамики процентной ставки 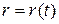, если в начальный момент 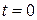она составляла .

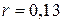Определить уровень процентной ставки в момент времени .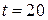

Решение. Из условия задачи следует, что 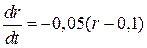. разделяя переменные в дифференциальном уравнении, получаем 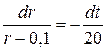. Интегрирование полученного уравнения

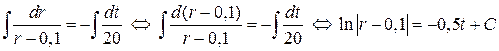
дает его общее решение 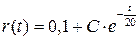. Использование начального условия 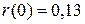позволяет найти значение константы.

.

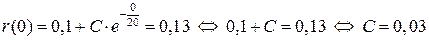Получаем уравнение динамики процентной ставки .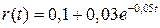

Тогда при 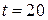получаем .

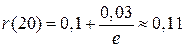Ответ: ; .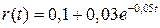

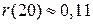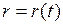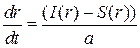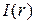Задача 20.Динамика процентной ставки в классической макромодели определяется уравнением ,где –функцияинвестиций, 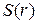– функция сбережений, а – параметр.

Вывести уравнение динамики процентной ставки 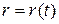, если в начальный момент 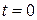она составляет .

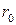20.1. ;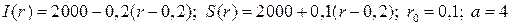

20.2. ;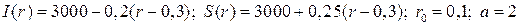

20.3. ;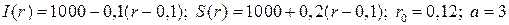

20.4. ;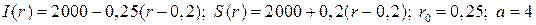

20.5. ;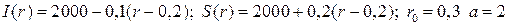

20.6. ;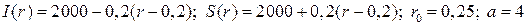

20.7. ;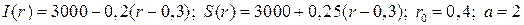

20.8. ;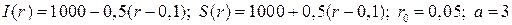

20.9. ;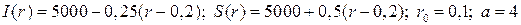

20.10. .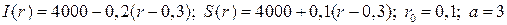

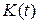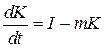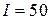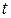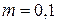Пример 21. Динамика основных производственных фондов (ОПФ) отрасли определяется дифференциальным уравнением , где ден. ед. – объём инвестиций в момент времени , а – коэффициент выбытия основных фондов. В начальный момент времени 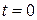объём фондов составлял 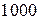ед.

Найти стационарное решение уравнения .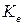

Вывести уравнение динамики основных производственных фондов .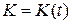

Построить график функции .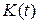

Решение. Найдем стационарное решение уравнения : .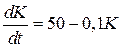

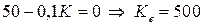Уравнение динамики ОПФ можно записать в виде 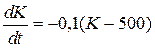. разделяя переменные в дифференциальном уравнении, получаем .

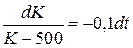Интегрируя полученное уравнение

,

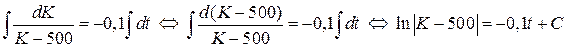получаем его общее решение .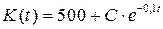

Использование начального условия 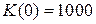позволяет найти уравнение динамики основных производственных фондов .

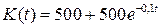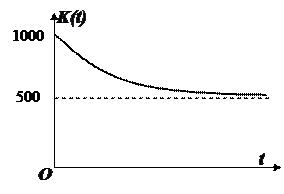Для построения графика функции 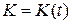заметим, что 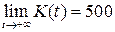, т.е. прямая 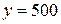является горизонтальной асимптотой графика функции справа. Вычислим знаки первой и второй производных функции: 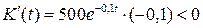, т.е. 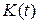всюду убывает; 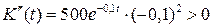, т.е. функция выпукла вниз всюду. График функции 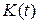представлен ниже.

Ответ: 1) 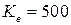; 2) .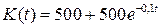

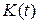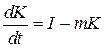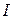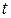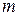Задача 21.Динамика основных производственных фондов (ОПФ) отрасли определяется дифференциальным уравнением , где – объём инвестиций в момент времени , а – коэффициент выбытия основных фондов. В начальный момент времени 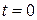объём фондов составлял 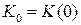ед.

Найти стационарное решение уравнения .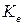

Вывести уравнение динамики основных производственных фондов .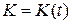

Построить график функции .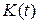

21.1.	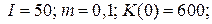21.6.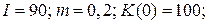
21.2.	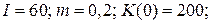21.7.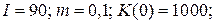
21.3.	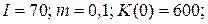21.8.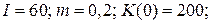
21.4.	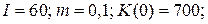21.9.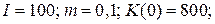
21.5.	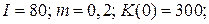21.10. .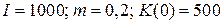

Ответственность за сведения, представленные в издании, несут авторы.

Учебное издание