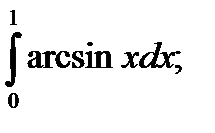Основні формули інтегрування
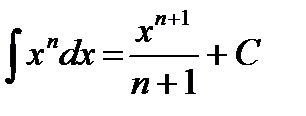 (n¹-1) , у тому числі
(n¹-1) , у тому числі
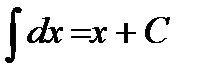 ;
;
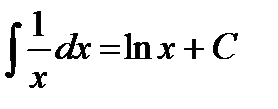 ;
;
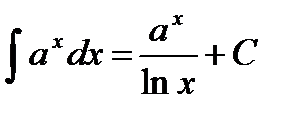 , у тому числі
, у тому числі 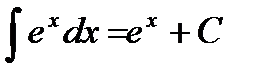 ;
;
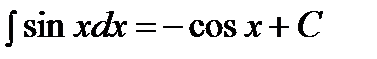 ;
;
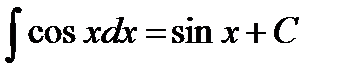 ;
;
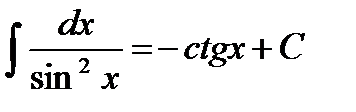 ;
;
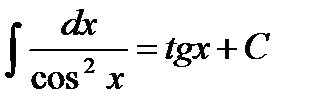 ;
;
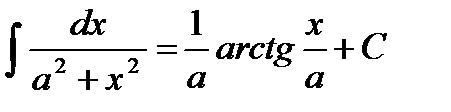 , у тому числі
, у тому числі 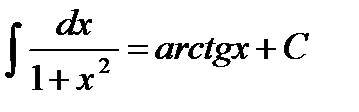 ;
;
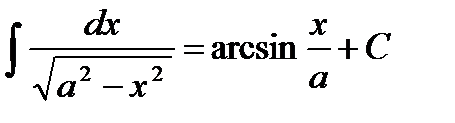 , у тому числі
, у тому числі 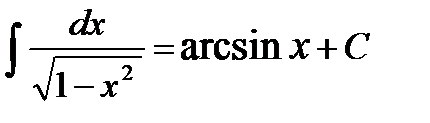 ;
;
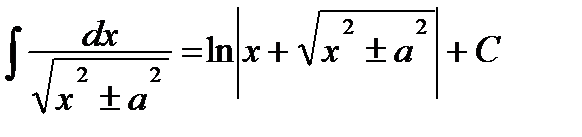 .
.
Із означення невизначеного інтеграла випливають такі властивості інтегрування:
1) 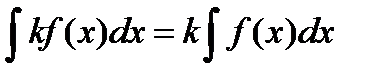 ;
;
2) 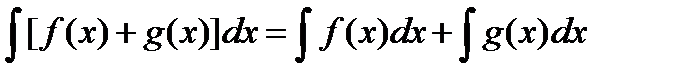 ;
;
3) 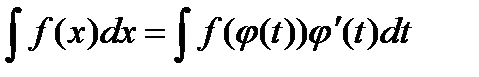 (метод заміни змінних, метод підстановки);
(метод заміни змінних, метод підстановки);
4) 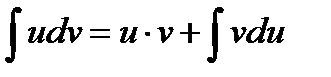 (інтегрування частинами).
(інтегрування частинами).
Задача 1. Обчислити невизначені інтеграли методом підстановки:
а) 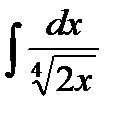 ; б)
; б) 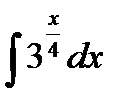 ; в)
; в) 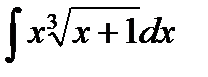 ; г)
; г) 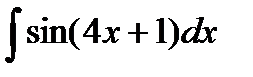 ;д)
;д) 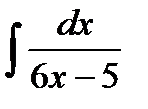
Задача2. . Обчислити невизначені інтеграли методом інтегрування частинами:
а) 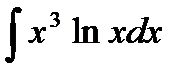 ; б)
; б) 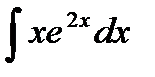 ; в)
; в) 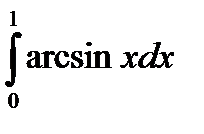
Питання для самоконтролю знань, умінь
1. Що таке первісна функції? Необхідна умова існування первісної.
2. Що таке невизначений інтеграл?
3. Властивості невизначеного інтегралу.
4. Правила інтегрування
5. Метод заміни змінної (підстановки) обчислення невизначених інтегралів.
6. Метод інтегрування частинами у невизначеному інтегралів.
Висновок. _________________________________________________________
__________________________________________________________________
Перевірив викладач ___________ Оцінка ___________ Дата___________
ПРАКТИЧНА РОБОТА № 14
Тема. Розв’язування задач на обчислення визначених інтегралів частинами та заміною змінних
Мета роботи:Навчитись обчислювати визначені інтеграли частинами та заміною змінних.
Наочне забезпечення та обладнання:
1. Інструкційні картки
2. Приклади задач
3. Роздаткові матеріали: опорні конспекти “Основні формули інтегрування”
4. Обчислювальні засоби: калькулятор.

Теоретичні відомості про правила інтегрування та застосування визначеного інтегралу.
Визначений інтеграл та методи його обчислення
Формула Ньютона – Лейбніца.
Для обчислення визначеного інтеграла від функції 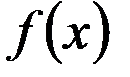 в тому випадку, коли можна знайти відповідний невизначений інтеграл
в тому випадку, коли можна знайти відповідний невизначений інтеграл 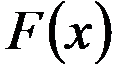 , є формула Ньютона – Лейбніца:
, є формула Ньютона – Лейбніца:  ,
,
тобто визначений інтеграл дорівнює різниці значень первісної при верхній і нижній межах інтегрування.
Метод підстановки у визначеному інтегралі.
1. Метод підстановки у визначеному інтегралі дає можливість звести інтегрування складеної функції до інтегрування табличної функції. Метод підстановки опирається на формулу диференціювання складеної функції.
2. Метод підстановки у визначеному інтегралі відрізняється від методу підстановки у невизначеному тим, що ми після обчислення інтегралу не повертаємось до старої змінної інтегрування, оскільки змінюємо межі інтегрування.
Метод інтегрування частинами у визначеному інтегралі.
1. Інтегрування частинами у визначеному інтегралі базується на формулі похідної добутку:
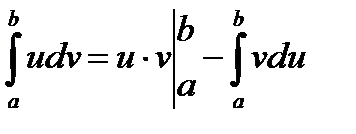
2. Для інтегрування виразів виду:
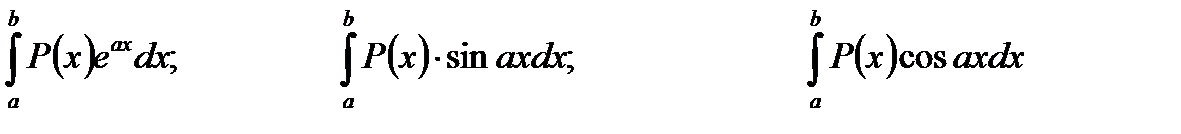 ,
,
де Р(х) – многочлен u слід приймати многочлен, що допоможе знизити його степінь.
Для інтегралів виду 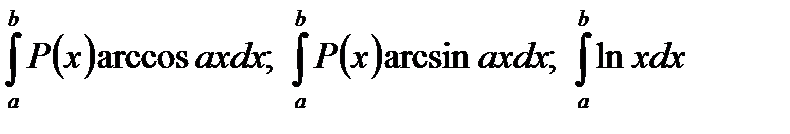 доцільно за u приймати функції arcсosx, arcsinx та lnx, а за dv вираз Р(х).
доцільно за u приймати функції arcсosx, arcsinx та lnx, а за dv вираз Р(х).
Завдання 1. Обчислити визначені інтеграли:
а) 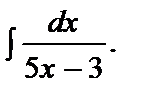 ; б)
; б) 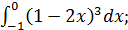 в)
в) 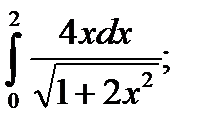
а) 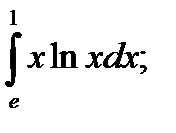 б)
б) 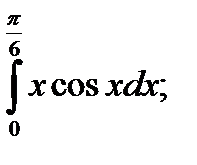 в)
в)