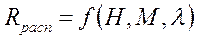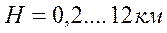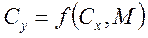Система уравнений движения
Углы, определяющие положение летательного аппарата относительно вектора скорости
Угол атаки α - угол между связанной осью 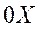 и проекцией вектора скорости на плоскость симметрии ЛА.
и проекцией вектора скорости на плоскость симметрии ЛА.
Угол скольжения β - угол между вектором скорости и плоскостью симметрии ЛА. Знаки углов атаки и скольжения определены на рис. 4.
Углы, определяющие положение летательного аппарата относительно Земли
По определению нормальной и связанной систем координат положение ЛА относительно Земли определяется углами между осями связанной и нормальной системы координат.
Угол тангажа υ–угол между связанной осью 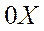 и горизонтальной плоскостью
и горизонтальной плоскостью 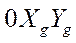 ;
;
Угол рыскания ψ –угол между осью 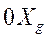 и проекцией связанной оси
и проекцией связанной оси 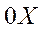 на горизонтальную плоскость
на горизонтальную плоскость 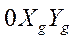 ;
;
| |
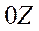 и осью
и осью 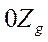 смещенной в положение, соответствующее нулевому углу рыскания.
смещенной в положение, соответствующее нулевому углу рыскания. Знаки углов определены на рис. 3.
Воздушная скорость 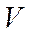 летательного аппарата – скорость центра масс (начала О связанной системы координат) относительно воздушной среды, не возмущенной летательным аппаратом.
летательного аппарата – скорость центра масс (начала О связанной системы координат) относительно воздушной среды, не возмущенной летательным аппаратом.
Земная скорость летательного аппарата 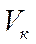 – скорость центра масс (начала О связанной системы координат) относительно выбранной земной системы координат.
– скорость центра масс (начала О связанной системы координат) относительно выбранной земной системы координат.
Путевая скорость летательного аппарата 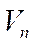 – проекция земной скорости летательного аппарата на горизонтальную плоскость.
– проекция земной скорости летательного аппарата на горизонтальную плоскость.
Траекторные углы
Угол пути ψ – угол между осью 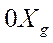 и путевой скоростью
и путевой скоростью 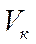 летательного аппарата (рис.5)
летательного аппарата (рис.5)
В продольном движении центра масс на самолет как на любое тело, действуют четыре силы, условно приложенные в центре масс. Эти силы фактически являются суммой сил, действующих на различные элементы самолета.
| |
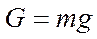 (земная система координат)
(земная система координат) 2. Подъемная сила 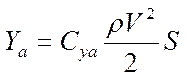 (скоростная с-ма координат)
(скоростная с-ма координат)
3. Сила сопротивления 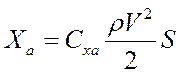 (скорост. с-ма координат)
(скорост. с-ма координат)
4. Сила тяги двигателей 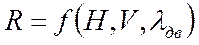 (связанная система)
(связанная система)
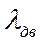 - режим работы двигателей.
- режим работы двигателей.
Система уравнений движения
Уравнения движения записываются в проекциях на скоростную систему координат
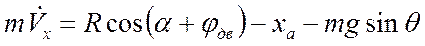 | 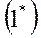 |
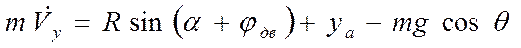 | 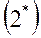 |
Поскольку 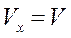 ,
, 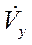 равно центростремительному ускорению
равно центростремительному ускорению
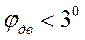 - мал,
- мал, 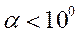 - мал, то уравнения (1), (2) можно переписать в виде:
- мал, то уравнения (1), (2) можно переписать в виде:
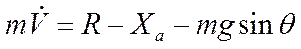 | 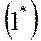 |
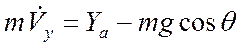 | 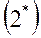 |
Для определения ЛТХ нужно добавить переход от скоростной системы к земной, а также отдельное уравнение для расхода топлива.
| |
Получим систему из дифференциальных уравнений (опуская индекс «а», т.е. 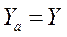 ,
, 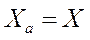 ):
):
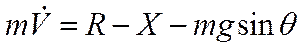 | 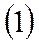 |
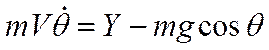 | 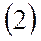 |
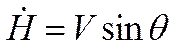 | 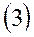 |
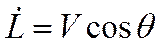 | 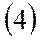 |
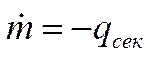 |  |
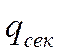 - секундный расход топлива двигателя, задается в виде:
- секундный расход топлива двигателя, задается в виде:
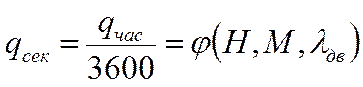 ,
, 
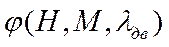 - данные моторного завода.
- данные моторного завода.
Из решения уравнений (1)-(6) можно найти показатели ЛТХ: 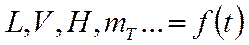 .
.
Эти уравнения решаются, как правило, методами численного интегрирования, для чего необходимо записать еще ряд аналитических и графических зависимостей:
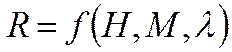 | 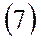 | ||
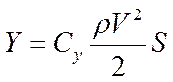 | 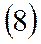 | ||
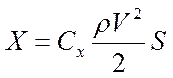 | 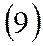 | ||
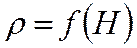 - стандартная атмосфера - стандартная атмосфера | 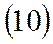 | ||
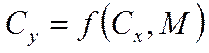 | 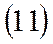 | ||
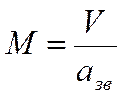 | 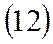 | ||
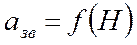 - стандартная атмосфера, скорость звука - стандартная атмосфера, скорость звука | 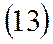 |
 |
|
 |
Система уравнений (1) – (13) содержит 15 неизвестных, т.е. две неизвестных должны быть заданы и называются управлениями. Для типового профиля полета задаются:
1)
| |
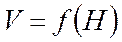 ,
, 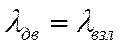 .
. 2) Набор высоты: 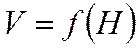 ,
, 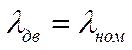 .
.
3) Крейсерский полет: а.) 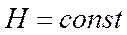 ,
, 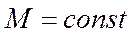 ,
,
б.) 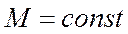 ,
, 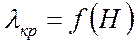 .
.
4) Снижение (планирование): 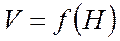 ,
, 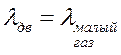 .
.
5) Заход на посадку: 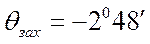 ,
, 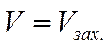 .
.
На предварительных этапах проектирования система уравнений (1) – (13) обычно решается приближенными методами. Для этого вводятся допущения для режимов 2, 3, 4: 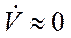 ,
, 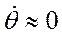 . Параметры скорость
. Параметры скорость 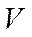 и угол наклона траектории
и угол наклона траектории 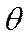 меняются медленно для транспортных магистральных самолетов. Кроме того, в ряде случаев можно считать, что угол
меняются медленно для транспортных магистральных самолетов. Кроме того, в ряде случаев можно считать, что угол 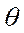 мал, т.е.
мал, т.е. 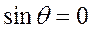 ,
, 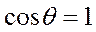 .
.
| |
Расчет основных ЛТХ включает:
- определение эксплуатационной области высот и скоростей полета: максимальной и минимальной скорости, практического потолка;
- расчет расхода топлива, времени и дальности полета на участках набора крейсерской высоты 2, снижения 4, крейсерского полета 3, в том числе расхода топлива на взлет 1, предпосадочный круг и посадку 5. (рис. - типовой профиль полета);
- определение общей практической дальности и продолжительности полета.
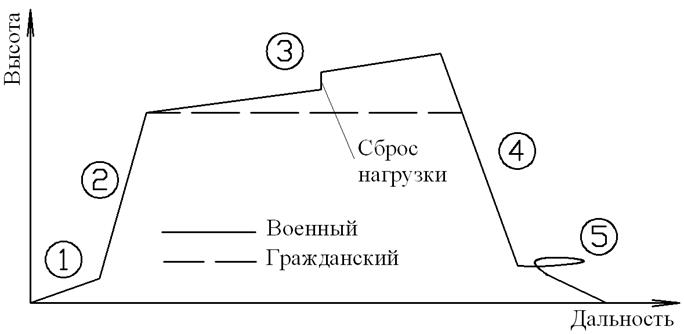
Типовой профиль полета
| |
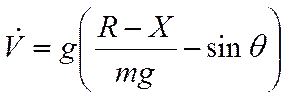 | 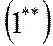 |
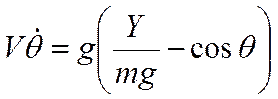 | 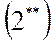 |
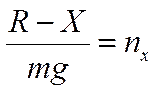 - продольная перегрузка,
- продольная перегрузка,
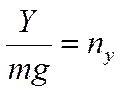 - поперечная перегрузка.
- поперечная перегрузка.
Тогда получим уравнения движения, выраженные через перегрузки:
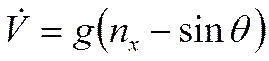 | 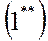 |
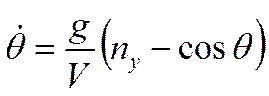 | 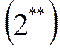 |
Остальные уравнения (3)-(13) остаются в том же виде.
Упрощение уравнений (1) и (2)
|
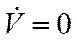 | 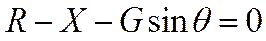 | |
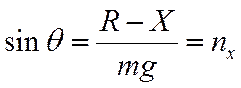 | 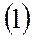 | |
Т.к. 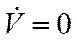 , , | уравнение описывает набор высоты с постоянной скоростью 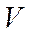 |
Умножим обе части уравнения (1) на 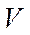 :
:
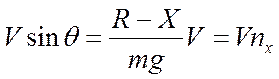 | 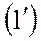 |
В уравнении 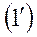 величина
величина 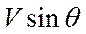 по внешнему виду соответствует
по внешнему виду соответствует 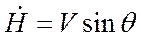 в уравнении
в уравнении 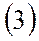 , однако в уравнении
, однако в уравнении 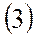
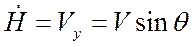 описывает вертикальную скорость набора высоты в общем виде (при
описывает вертикальную скорость набора высоты в общем виде (при 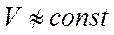 ). В уравнении
). В уравнении 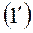 величина
величина
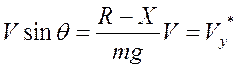 описывает «фиктивную» вертикальную скорость набора высоты
описывает «фиктивную» вертикальную скорость набора высоты 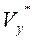 (ее называют также избыточной удельной мощностью)
(ее называют также избыточной удельной мощностью) 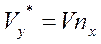 упрощение
упрощение 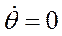 приводит уравнение
приводит уравнение 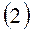 к виду
к виду 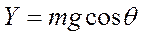 или
или 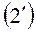
| |
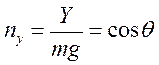 (
( 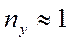 ,
, 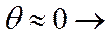 полет горизонтальный).
полет горизонтальный). Это условие соответствует «квази»-горизонтальному полету с постоянной скоростью (т.к. 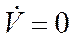 ).
).
Таким образом, для участков профиля полета 2 – набор высоты, 3 – крейсерский полет 4 – снижение для расчетов параметров 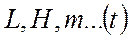 можно принять упрощенные уравнения
можно принять упрощенные уравнения 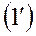 и
и 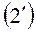 , если объектами являются достаточно большие, медленно маневрирующие транспортные самолеты, у которых
, если объектами являются достаточно большие, медленно маневрирующие транспортные самолеты, у которых 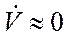 и
и 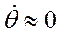 .
.
И уравнения (1) и (2) из дифференциальных превращаются в алгебраические
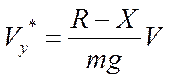 или или 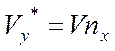 | 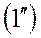 |
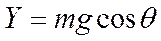 или или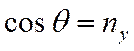 | 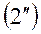 |
Остальные уравнения остаются в прежнем виде.
Первым этапом расчетов является построение совмещенных графиков потребных тяг (сопротивления самолета) и располагаемых тяг силовой установки. В уравнении 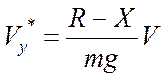 ,
,
где 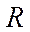 - располагаемая тяга двигателя,
- располагаемая тяга двигателя,
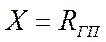 - тяга, потребная для горизонтального полета.
- тяга, потребная для горизонтального полета.
| |
| Масса | 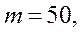 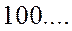 т т | ||||
| Высота | 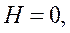 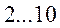 км км | ||||
| Скорость звука | 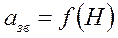 (м/c) (м/c) | ||||
| Плотность | 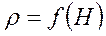 (кг/м3) (кг/м3) | ||||
|
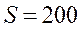 м2 м2 |
|
 |
| |
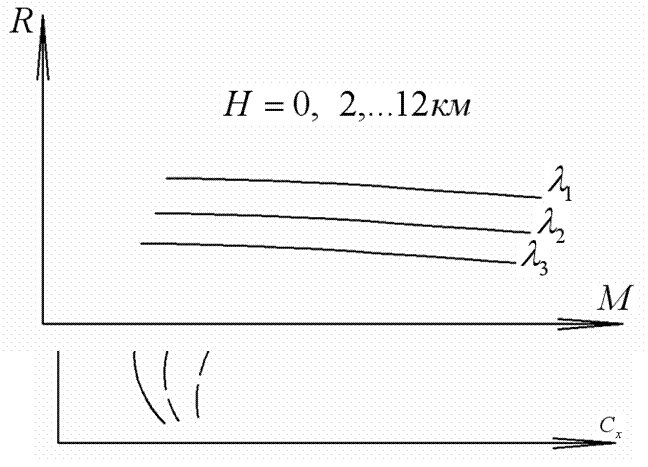
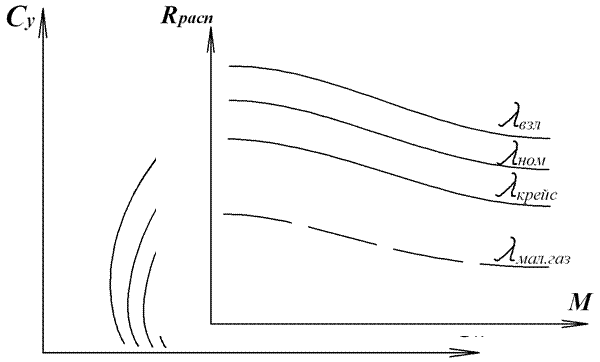
Для расчетов используется метод совмещения располагаемых тяг двигателя на номинальном, максимальном бесфорсажном или форсажном режиме и тяг, потребных для горизонтального полета (метод тяг Н.Е. Жуковского).
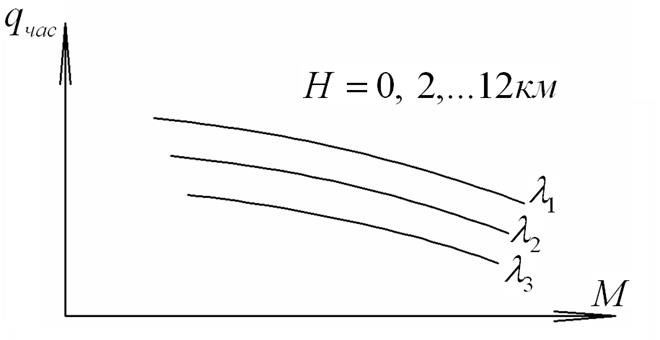
Тяги, потребные для горизонтального полета 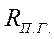 рассчитываются в зависимости от числа
рассчитываются в зависимости от числа 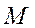 для ряда значений высот и среднего полетного веса
для ряда значений высот и среднего полетного веса 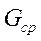 или для ряда значений веса
или для ряда значений веса 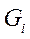 .
.
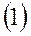 |
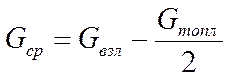 ,
,
где:
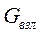 | - взлетный вес |
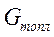 | - вес топлива |
Например, для дозвукового пассажирского самолета могут быть взяты высоты 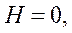
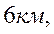
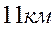 (или другие).
(или другие).
Расчет производится по упрощенному методу тяг [1].
Тяга, потребная для горизонтального полета:
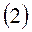 |
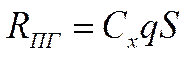 ,
,
где:
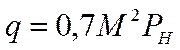 - скоростной напор (или
- скоростной напор (или 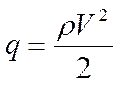 );
);
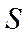 - площадь крыла;
- площадь крыла;
| |
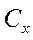 - определяется по поляре для соответствующего числа
- определяется по поляре для соответствующего числа 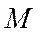 для значений
для значений 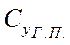 , определяемых формулой
, определяемых формулой 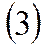 |
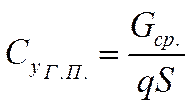 или
или 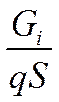 .
.
Результаты расчетов сводятся в таблицу №1
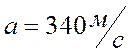
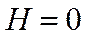
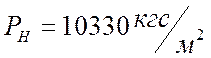
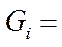
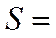
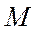 | 0,3 | 0,5 | 0,7 | 0,9 | Примечание | |
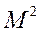 | 0,09 | 0,25 | 0,49 | 0,81 | ||
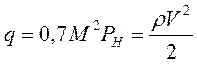 | Скоростной напор | |||||
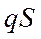 | ||||||
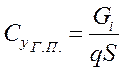 | ||||||
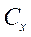 (в поляре) (в поляре) | ||||||
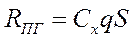 | ||||||
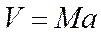 | 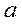 - скорость звука - скорость звука | |||||
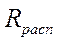 | ||||||
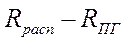 | ||||||
 |
|
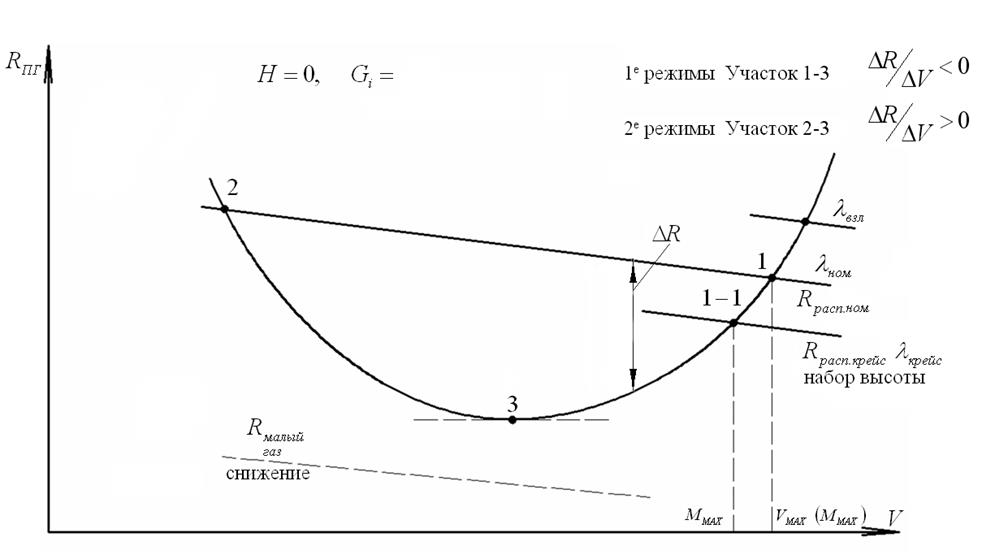
По данным таблицы №1 строится график
| |
 (см. рис. ) на заданном режиме работы двигателя (
(см. рис. ) на заданном режиме работы двигателя ( 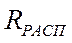 ).
). Аналогичные таблицы и графики строятся для других значений высоты полета при той же величине выбранного веса 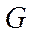 . Затем расчеты повторяются для других весов.
. Затем расчеты повторяются для других весов.
Точки пересечения линий 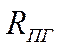 и
и 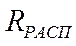 . Определят на каждой высоте
. Определят на каждой высоте 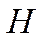 максимальную скорость, т.е. правую границу области полета.
максимальную скорость, т.е. правую границу области полета.
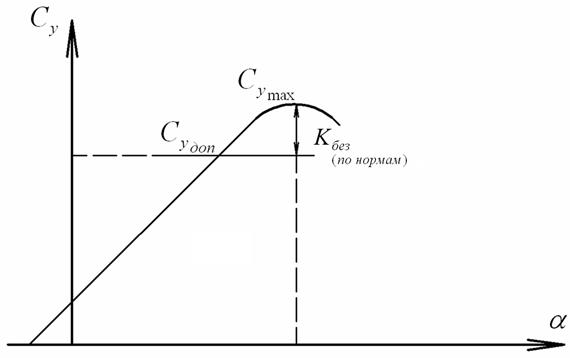
Левая граница области полета определяется значениями минимальных скоростей (чисел 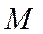 ), которые для каждой из заданных высот определяются по формуле:
), которые для каждой из заданных высот определяются по формуле:
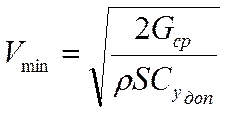 ,
,
где:
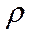 - скорость звука на заданной высоте;
- скорость звука на заданной высоте;
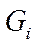 - заданный вес;
- заданный вес;
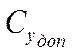 - по рис. ;
- по рис. ;
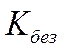 - коэффициент безопасности (по нормам).
- коэффициент безопасности (по нормам).
| |
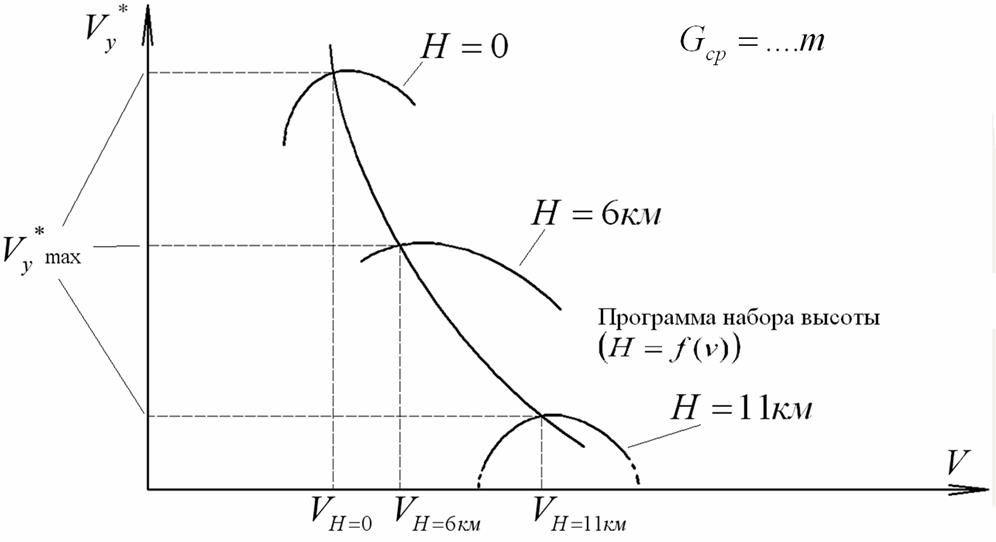
Диаграммы потребных и располагаемых тяг (рис.2) используются также для расчета скоростей установившегося набора высоты (или удельной избыточной мощности):
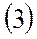 |
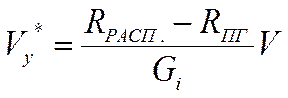
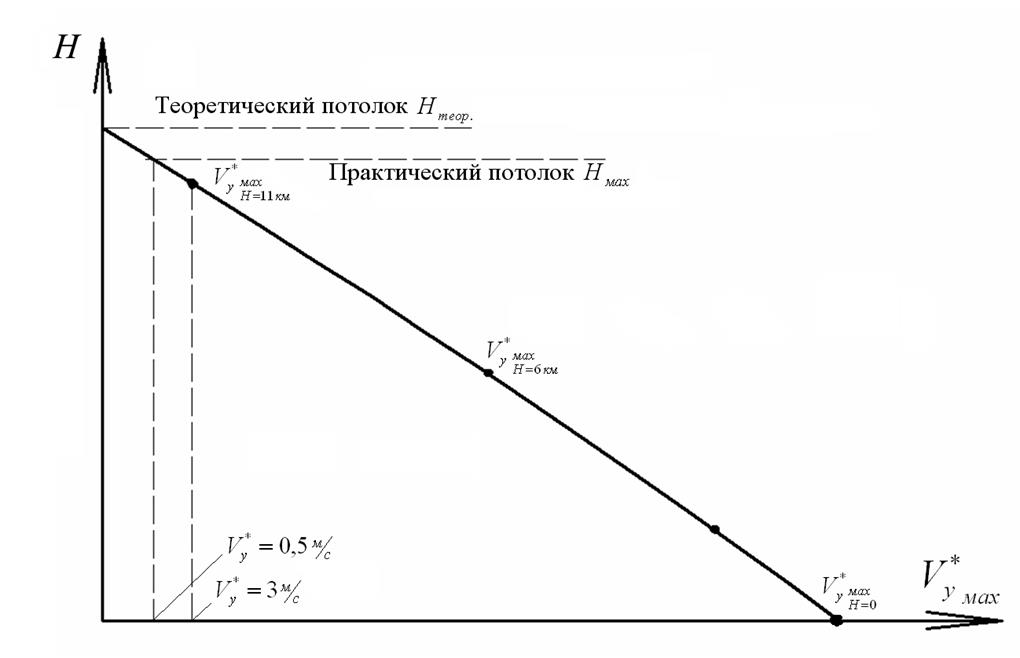
По графикам 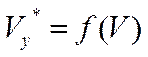 , рис. 4 для каждой из заданных высот определяются точки
, рис. 4 для каждой из заданных высот определяются точки 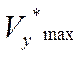 , соответствующие максимальной скороподъемности, с помощью которых находится практический потолок
, соответствующие максимальной скороподъемности, с помощью которых находится практический потолок 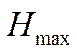 (рис. ), ограничивающий эксплуатационную область полета сверху, (рис. ), а также соответствующая величина скорости полета
(рис. ), ограничивающий эксплуатационную область полета сверху, (рис. ), а также соответствующая величина скорости полета 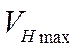 .
.
| |
| | |||||
| |||||
|
| |
| |
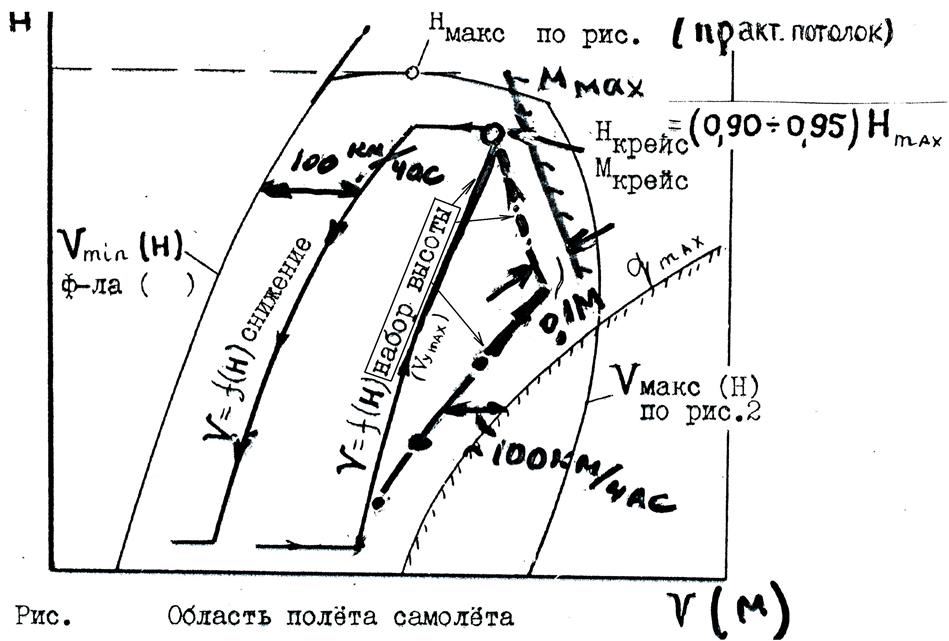
Внутри области полета с некоторым (нормированным) запасом от её границ намечаются оптимальные траектории набора высоты, крейсерского полета, снижения. Одна из возможных программ (траекторий) набора высоты 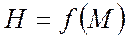 может быть найдена на рис. 4 – это точки
может быть найдена на рис. 4 – это точки 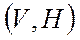 , соответствующие на каждой высоте
, соответствующие на каждой высоте 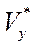 , т.е. режим максимальной скороподъемности. Он больше характерен для истребителей-перехватчиков. Для транспортных самолетов могут быть другие программы набора высоты, например,
, т.е. режим максимальной скороподъемности. Он больше характерен для истребителей-перехватчиков. Для транспортных самолетов могут быть другие программы набора высоты, например, 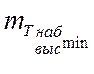 .
.
Для примера остановимся на программе (рис .4) 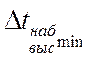 .
.
Как же летчик реализует эту траекторию (помним, что режим двигателя при наборе высоты задан 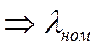 .
.
Практика показывает, что любые траектории в координатах 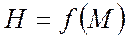 или
или 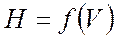 близки к тем или иным постоянным значениям скоростного напора
близки к тем или иным постоянным значениям скоростного напора 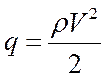 , которому можно условно приписать некоторую величину приборной скорости
, которому можно условно приписать некоторую величину приборной скорости 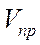 , (как известно из курса аэродинамики, скорость потока замеряется скоростной трубкой именно по величине
, (как известно из курса аэродинамики, скорость потока замеряется скоростной трубкой именно по величине 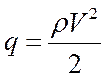 ), величина
), величина 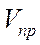 есть у летчика на приборе и ее достаточно просто поддерживать заданной (постоянной) управляя самолетом:
есть у летчика на приборе и ее достаточно просто поддерживать заданной (постоянной) управляя самолетом:
| |
- самолет отклонился вниз – тянуть «на себя»
- рычаг управления двигателем (РУД) не трогать!
Аналогично задается программа снижения и управление по ней.
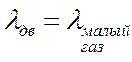 (рис.7).
(рис.7).
Можно включить автопилот.
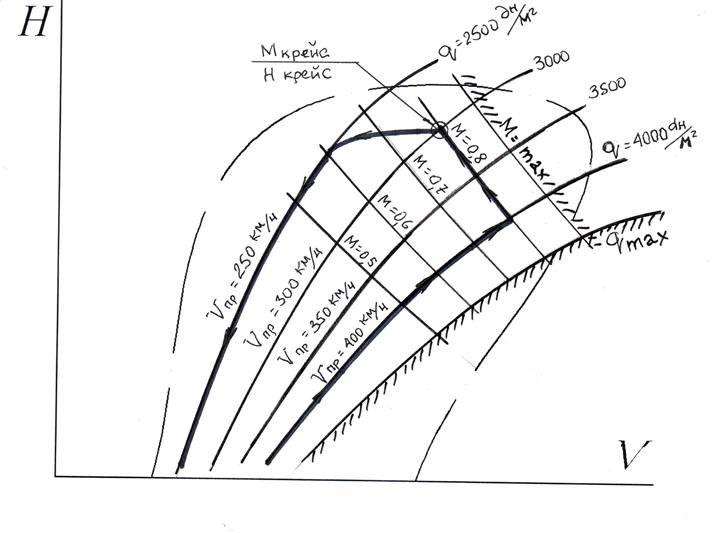
| |
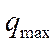 ), траектория набора высоты
), траектория набора высоты 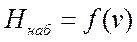 , соответствующая оптимальному режиму, в частности
, соответствующая оптимальному режиму, в частности 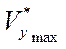 (рис. ), траектория снижения и другие ограничения (например,
(рис. ), траектория снижения и другие ограничения (например, 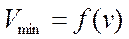 - формула стр. ).
- формула стр. ).