Задачи для самостоятельного решения. 1 Составить уравнение хорды окружности х2+у2 = 49, делящейся в точке А(1;2) пополам

1 Составить уравнение хорды окружности х²+у² = 49, делящейся в точке А(1;2) пополам.

Ответ.х + 2у -5 = 0.

2. Определить координаты центров и радиусы окружностей:

а) х²+у² - 8х + 6у = 0; б) х²+у²+10х- 4у+29 = 0;

в) х²+у²- 4х+14у + 54 = 0.

Ответ: а) а = 4, b=-3, r= 5; б) а = -5, b = 2, r=0. Уравнение определяет точку;

в) а =2, b=-7, r ²=-1. Уравнение не имеет геометрического смысла (мнимая, окружность).

3. Найти угол между радиусами окружности

х²+у²+4х-6у=0, проведенными в точки пересечения ее с осью Оу.

Ответ: tgφ=-2,4.

4. Составить уравнение окружности, проходящей через точки А(1; 2), В(0;-1), С(-3; 0).

Ответ: (х+1)²+(у -1)²=5.

5. Составить уравнение окружности, проходящей через точки А (7; 7) и В(-2; 4), зная, что ее центр лежит на прямой

2х- у-2=0.

Ответ: (х- З) ²+(у-4)²=25.

6. Составить уравнение общей хорды окружно­стей х²+у²=16 и (х -5)² + у² = 9.

Ответ: х=3,2.

7. Составить уравнение прямой, проходящей через левый фокус и нижнюю вершину эллипса .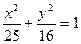

Ответ: 4х+3у+12= 0.

8. На прямой х+5=0 найти точку, одинаково удаленную от левого фокуса и верхней вершины эллипса .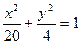

Ответ: М(—5; 7).

9. Пользуясь определением эллипса, составить его уравнение, зная, что точки F₁ (0; 0) и F₂ (1; 1) явля­ются фокусами эллипса, а длина большой оси равна 2.

Ответ: Зх² + Зу² - 2ху - 2х - 2у - 1 == 0.

10. Составить уравнение геометрического места точек, расстояния которых от точки А (0; 1) з два раза меньше расстояния до прямой у—4=0.

Ответ: .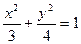

.

Занятие 16. Кривые второго порядка: гипербола, парабола

Гипербола.

Гиперболой называется геометрическое место точек, абсолютная величина разности расстояний которых до двух данных точек, называемых фокусами, есть величина постоянная (её обозначают через 2а), причем эта постоянная меньше расстояния между фокусами. Поместив фокусы гиперболы в точках F₁(с; 0) и F₂(-с;0), получаем уравнение гипер­болы в виде ,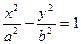

где b²=c²-a²;

это простейшее (каноническое) уравнение гиперболы. Гипербола состоит из двух ветвей и расположена симметрично относительно осей координат. Точки А₁(а;0) и А₂(-а;0) называются вершинами гиперболы.

Отрезок А₁А₂=2а называют вещественной осью гиперболы, а отрезок В₁В₂=2b – мнимой осью (рис. 15).

Прямая называется асимптотой гиперболы, если расстояние точки гиперболы М (х;у) от этой прямой стремится к нулю при х→+∞ или х→-∞. Гипербола имеет две асимптоты, уравнения которых 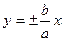.Для построения асимптот гиперболы строят осевой прямоугольник гиперболы со сторонами х=а,

х = - а, у=b, у=-b. Прямые, проходящие через противоположные вершины этого прямоугольника, являются асимптотами гиперболы. На чертеже указано взаимное расположение гиперболы и ее асимптот. Отношение ε 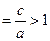называется эксцентриситетом гиперболы.

Если а=b, то уравнение гиперболы принимает вид

х²- у² = a².

Такая гипербола называется равнобочной.

Уравнение

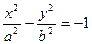(или )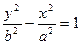

также является уравнением гиперболы, но вещественной осью этой гиперболы служит отрезок оси Оу длины 2b.

Две гиперболы 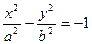и 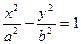имеют одни и те же полуоси и одни и те же асимптоты; но вещественная ось одной служит мнимой осью другой, и наоборот. Такие две гиперболы называются сопряженными.

Пример 16.1.Эксцентриситет гиперболы равен 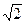. Соста­вить простейшее уравнение гиперболы, проходящей через точку М( ; ).

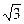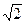Решение. По определению эксцентриситета можем написать равенство 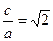, или с²=2а². Но с² = а²+ b², следовательно, а² + b² = 2а², или а²= b², т. е. гипербола равнобочная.

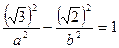Другое равенство имеем из условия нахождения точки М на гиперболе, т. е. , или 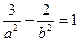. Поскольку а²=b², получим 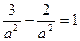, т.е. а²=1.

Таким образом, уравнение искомой гиперболы имеет вид х²- у²=1.

Парабола.

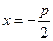Параболой называется геометрическое место точек, равноудаленных от данной точки, называемой фокусом, и данной прямой, называемой директрисой. Если директрисой параболы является прямая , а фокусом - точка 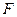( 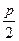,0), то уравнение параболы имеет вид

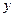
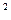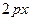= . (16.1)

Эта парабола расположена симметрично относительно оси абсцисс (рис.6, где р 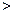0).

Уравнение

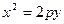(16.2)

является уравнение параболы, симметричной относительно оси ординат. При p>0 параболы (16.1) и (16.2) обращены в положительную сторону соответствующей оси, а при p<0 - в отрицательную сторону. Длина фокального радиуса-вектора параболы 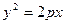определяется по формуле .

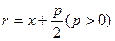Пример 16.2. Составить уравнение параболы, симметричной относительно оси 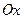, с вершиной в начале координат, если длина некоторой хорды этой параболы, перпендикулярной к оси Ох, равны 16, а расстояние этой хорды от вершины равно 6.

Решение. Поскольку известны длина хорды и расстояние ее от вершины, то, следовательно , известны координаты конца этой хорды-точки М, лежащей на параболе. Уравнение параболы имеет вид 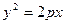; пологая в нем 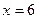, , 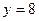находим 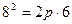,откуда .

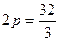Таким образом, уравнение искомой параболы .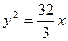

Пример 16.3. Составить уравнение параболы с вершиной в начале координат, симметричной относительно оси Оу и отсекающей на биссектрисе 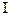и 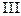координатных углов хорду длиной .

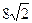Решение. Искомое уравнение параболы 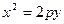, уравнение биссектрисы 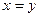. Следовательно, точками пересечения параболы с биссектрисой будут О(0;0) и М(2р;2p).

Длина хорды определяется как расстояние между двумя точками 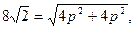откуда 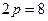.Следовательно , уравнение искомой параболы имеет вид .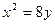